
- •Раздел I. Элементы линейной и векторной алгебры Основы аналитической геометрии
- •Глава 1. Элементы линейной алгебры
- •1.1. Матрицы и операции над ними
- •1.3. Обратная матрица. Решение матричных уравнений
- •1.4. Ранг матрицы
- •1.6. Система линейных однородных уравнений. Фундаментальная система решений
- •1.7. Контрольные задания к главе 1
- •Глава 2. Элементы векторной алгебры
- •2.1. Векторы на плоскости и в пространстве
- •2.2. Проекция вектора на ось. Скалярное произведение векторов
- •2.3. Векторное и смешанное произведения векторов
- •2.5. Задачи с экономическим содержанием к главам 1, 2
- •2.6. Контрольные задания к главе 2
- •Глава 3. Основы аналитической геометрии
- •3.1. Простейшие задачи аналитической геометрии на плоскости
- •3.2. Прямая линия на плоскости
- •3.4. Прямая и плоскость в пространстве
- •3.5. Понятие гиперплоскости. Выпуклые множества
- •3.6. Контрольные задания к главе 3
- •Раздел II. Введение в математический анализ
- •Глава 4. Функция одной переменной
- •4.1. Функциональная зависимость и способы ее представления
- •4.2. Элементарные функции. Преобразование графиков функций
- •Глава 5. Пределы и непрерывность
- •5.1. Числовая последовательность
- •5.2. Предел последовательности
- •5.3. Предел функции. Раскрытие простейших неопределенностей
- •5.4. Замечательные пределы
- •5.5. Сравнение бесконечно малых
- •5.6. Односторонние пределы
- •5.7. Непрерывность и точки разрыва функции
- •5.8. Контрольные задания к разделу II
- •Глава 6. Производная и дифференциал
- •6.1. Определение производной. Правила дифференцирования
- •6.2. Производная сложной функции
- •6.3 Логарифмическая производная и производная неявной функции
- •6.4. Геометрический и механический смысл производной. Производные высших порядков
- •6.6. Контрольные задания к главе 6
- •Глава 7. Приложения производной
- •7.1. Теорема о среднем значении. Формула Тейлора
- •7.2. Правило Лопиталя-Бернулли
- •7.4. Выпуклость (вогнутость) графика функции. Точки перегиба
- •7.5. Асимптоты. Построение графиков функций
- •7.7. Контрольные задания к главе 7
- •Примерные варианты тестовых заданий
- •ОТВЕТЫ
- •Глава 1
- •Глава 2
- •Глава 3
- •Глава 4
- •Глава 5
- •Глава 6
- •Глава 7
- •Содержание
7.124. Консервная банка данного объема V = 250π см3 должна иметь форму цилиндра. Каковы должны быть ее размеры (высота Н и диаметр D) чтобы на ее изготовление ушло наименьшее количество жести?
7.125. Какими должны быть размеры открытого бассейна с квадратным дном и объемом 32 м3, чтобы на облицовку плиткой стен и дна бассейна ушло наименьшее количество материала?
7.4. Выпуклость (вогнутость) графика функции. Точки перегиба
График дифференцируемой функции y = f (x) называется выпуклым на интервале (а, b), если дуга кривой на этом интервале расположена ниже касательной, проведенной к графику функции в любой точке x (a,b) . Если на ин-
тервале (а, b) любая касательная располагается ниже дуги кривой графика функции, то он называется вогнутым на данном интервале.
Точка (x0 , f (x0 )), в которой выпуклость меняется на вогнутость или на-
оборот, называется точкой перегиба.
Достаточное условие выпуклости (вогнутости) графика |
функции. |
||
Если функция |
y = f (x) дважды дифференцируема на интервале (а, |
b) и для |
|
всех x (a,b) f |
′′ |
′′ |
|
(x) < 0 |
(f (x) > 0), то функция выпукла (вогнута) на интервале |
||
(а, b).
Достаточное условие точки перегиба. Если в точке x0 вторая произ-
водная f ′′(x0 ) = 0 или не существует и при этом при переходе через точку x0
меняет знак, то точка x0 является точкой перегиба функции y = f (x) .
Пример 7.10. Найти интервалы выпуклости, вогнутости функции y = ln(1 + x2 ) и точки перегиба.
284

|
Р е ш е |
н и е. Найдем вторую производную |
функции y′ = |
2x |
, |
|
1 + x2 |
||||
y′′ = |
2(1 − x2 ) |
|
х и равна нулю при |
||
(1 + x2 )2 . |
Вторая производная существует при всех |
||||
x = ±1. Нанесем на числовую ось точки x = ±1 и определим на полученных интервалах знаки второй производной.
– |
D |
+ |
D |
– |
|
–1 |
|
1 |
х |
Функция выпукла на промежутках (−∞; −1) и (1; + ∞) и вогнута на промежутке
(–1; 1). В точках x = ±1 вторая производная функции равна нулю и меняет знак, следовательно, эти точки являются точками перегиба.
Задачи для самостоятельного решения
Найти интервалы выпуклости, вогнутости точки перегиба кривых.
7.126. y = x3 −3x2 + 4x −1; |
7.127. y = x4 − 6x2 + x; |
||||||||||||||||
7.128. y = 3x5 −5x4 + 2x + 3; |
7.129. y = x + 36x2 − 2x3 − x4 ; |
||||||||||||||||
7.130. y = |
2x2 |
+ 4 |
; |
|
7.131. |
y = |
x2 |
+ |
2x + 4 |
; |
|||||||
x2 |
− |
4 |
|
|
x |
+ 2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
7.132. y = x |
−4 |
− |
8x |
−2 |
; |
7.133. |
y = |
|
x4 |
− x +1 |
; |
|
|||||
|
|
|
x3 −1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7.134. y = x e−x2 ; |
|
|
|
7.135. y = (x +1)e−x ; |
|
||||||||||||
7.136. y = x2 + 2 ln x; |
7.137. |
y = |
ln x |
; |
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
7.138. y = ln(x2 −1); |
|
7.139. y = x2 ln x; |
|
|
|||||||||||||
7.140. y = 4 − 3 |
x −1; |
7.141. y = 2 + 5 |
(x − 4)3 ; |
||||||||||||||
7.142. y = x +8 4 x3 ; |
7.143. y = 3 x +1 −3 x −1. |
||||||||||||||||
285
7.5. Асимптоты. Построение графиков функций
Прямая y = kx + b называется наклонной асимптотой графика функции
y = f (x) , если расстояние от точки M (x, f (x)) до данной прямой стремится к нулю при удалении точки М в бесконечность.
Если существуют конечные пределы k = lim |
f (x) |
, |
b = lim ( f (x) − kx) , |
|
x |
||||
x→+∞ |
|
x→+∞ |
то прямая y = kx + b является наклонной асимптотой графика функции при x → +∞. Если существуют аналогичные пределы x → −∞, то прямая y = kx + b
является наклонной асимптотой графика функции при x → −∞ . Следует отметить, что асимптоты при x → +∞ и при x → −∞ могут быть различными.
Прямая x = x0 является вертикальной асимптотой графика функции y = f (x) , если хотя бы один из односторонних пределов функции в точке x0
равен бесконечности.
Для исследования функции и построения ее графика может использоваться следующая схема:
1)найти область определения функции;
2)определить четность (нечетность) функции, ее периодичность;
3)найти точки разрыва функции, ее вертикальные асимптоты;
4)найти точки перегиба с осями координат;
5)найти интервалы возрастания, убывания функции и ее экстремумы;
6)найти интервалы выпуклости, вогнутости функции, точки перегиба;
7)найти наклонные асимптоты графика функции;
8)построить график функции.
Пример 7.11. Найти асимптоты графика функции |
y = |
2x2 |
− x |
+1 |
. |
|||
x −1 |
|
|||||||
|
|
|
|
|
|
|||
Ре ш е н и е. Так как lim |
2x2 − x +1 |
= +∞ , а lim |
2x2 − x +1 |
= −∞, полу- |
||||
x −1 |
x −1 |
|
||||||
x→1+0 |
x→1−0 |
|
|
|
|
|||
чаем, что прямая х = 1 является вертикальной асимптотой.
286

|
Найдем наклонные асимптоты. lim |
f (x) |
= |
lim |
2x2 |
− x +1 |
= 2 |
= k . |
|||||
|
x |
x |
2 |
− x |
|
||||||||
|
|
|
|
x→±∞ |
x→±∞ |
|
|
||||||
lim (f (x) − kx)= lim |
x +1 |
|
=1. Так как пределы |
равны |
|
при x → +∞ и при |
|||||||
|
|
||||||||||||
x→±∞ |
x→±∞ x −1 |
|
|
|
|
|
|
|
|
|
|
||
x → −∞, то в обоих случаях наклонной асимптотой является у = 2х + 1.
Пример 7.12. Исследовать функцию y = x2x+1 и построить ее график .
Ре ш е н и е.
1)Область определения x (−∞; 0) (0; + ∞) .
2)Так как f (−x) = x2 +1 = − f (x) , функция является нечетной.
−x
3) |
Так как lim |
x2 |
+1 |
= +∞, lim |
x2 +1 |
= −∞, точка х = 0 является точкой раз- |
|||||||||
|
x |
|
|
x |
|
||||||||||
|
x→+0 |
|
|
x→−0 |
|
|
|
|
|
|
|||||
|
рыва второго рода, а прямая х = 0 – |
|
вертикальной асимптотой. В остальных |
||||||||||||
|
точках функция непрерывна. |
|
|
|
|
|
|
|
|
||||||
4) |
f (x) ≠ 0 ни при каких |
х. Точки пересечения с осью 0х отсутствуют, так как |
|||||||||||||
|
при х = 0 функция не определена. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
y |
′ |
|
x2 −1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
5) |
Найдем производную функции: |
= x2 |
. Производная равна нулю при |
||||||||||||
|
|||||||||||||||
|
x = ±1 и не определена при х = 0. Нанесем эти точки на ось 0х и определим |
||||||||||||||
|
знаки производной на полученных интервалах. Получим, что функция воз- |
||||||||||||||
|
растает на интервалах |
(−∞; −1) |
и (1; + ∞) , убывает на интервалах (–1; 0), (0; |
||||||||||||
1), точка х = –1 является точкой максимума функции, |
f (−1) = −2 , точка х = |
||||||
1 является точкой максимума, |
f (1) = 2 . |
|
|
|
|
||
+ |
–D1 |
– |
0D |
– |
D1 |
+ |
х |
6) Найдем вторую производную: |
y′′ = 2x−3 . Вторая производная не определена |
||||||
при х = 0 и нигде не равна нулю. Так как |
′′ |
|
′′ |
||||
y (x) < 0 при x < 0 и y (x) > 0 |
|||||||
при x > 0 , делаем заключение, что на интервале (−∞;0) функция выпукла,
на интервале (0; + ∞) – вогнута, точка х = 0 является точкой перегиба.
287

7) |
Найдем наклонные асимптоты: k = lim |
f (x) |
= lim |
x2 +1 |
=1, |
|||
x |
x2 |
|
||||||
|
|
x→±∞ |
x→±∞ |
|
||||
|
b = lim ( f (x) − kx) = lim 1 = 0 . Следовательно, |
уравнение наклонной |
||||||
|
x→±∞ |
x→±∞ x |
|
|
|
|
|
|
|
асимптоты имеет вид у = х. |
|
|
|
|
|
||
8) |
Используя полученные сведения, строим график функции (рис. 7.2). |
|||||||
у
2 • |
• |
–1
••
1х
•• –2
Рис. 7.2
Задачи для самостоятельного решения
|
Найти асимптоты кривых. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7.144. |
y = |
x + 2 |
; |
7.145. |
y = |
|
2x2 + x +1 |
; |
|
7.146. y = |
|
2x2 |
+ 3x |
; |
|||||||||
x |
−1 |
|
|
x − |
2 |
|
|
|
x2 |
+1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
7.147. y = |
|
2x |
2 |
7.148. |
y = |
|
x2 −1 |
|
|
|
7.149. y = |
|
|
x |
2 |
− x ; |
|
||||||
|
|
|
; |
|
|
|
|
|
; |
|
|
|
|
|
|
||||||||
x2 |
|
|
x |
2 + 2 |
|
|
|
|
|
|
|
||||||||||||
|
|
− 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7.150. y = x ex ; |
|
|
7.151. y = |
ln x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||
|
Построить графики функций. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7.152. y = x3 −3x2 +1; |
|
7.153. |
y = |
|
x |
|
; |
7.154. y = |
|
|
2x |
|
; |
|
|||||||||
|
|
|
|
1 |
− x2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 + x2 |
|
|
|
|
||||||||
288
7.155.
7.158.
7.161.
7.164.
7.164.
7.167.
7.170.
7.173.
7.176.
7.179.
7.182.
y = x + 1x ;
y= 3 − x2 ; x + 2
y = |
|
3x3 |
|
; |
|
x2 − |
3 |
||||
|
|
||||
y = 3 |
x2 |
− 2x ; |
|||
y = 3 |
x2 |
− 2x ; |
|||
y = |
x |
|
; |
||
|
|
x2 |
+ |
1 |
|
y = x e−x ;
y = xe−x2 ; y = lnxx ;
y = x ln x;
y = x − arctgx;
7.156. y = 4x2 + |
1 ; |
|
7.157. y = x3 + 6x2 +9x; |
||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.159. y = x |
5 |
|
−5x |
3 |
; |
|
7.160. |
y = |
|
x3 |
−3x |
; |
|
|
|||||||
|
|
|
|
|
x |
3 − |
1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7.162. y = |
|
|
4 |
|
; |
|
|
|
7.163. |
y = |
x |
+ |
3 |
; |
|
|
|
|
|||
1 |
+ x2 |
|
|
|
|
|
|
3 |
|
|
x |
|
|
|
|
|
|||||
7.165. y = 3 |
x +1 − 3 |
x −1; |
7.166. y = 3 1 − x3 ; |
|
|
||||||||||||||||
7.165. y = 3 |
x +1 − 3 |
x −1; |
7.166. y = 3 1 − x3 ; |
|
|
||||||||||||||||
7.168. y = |
|
x2 |
|
; |
|
7.169. y = x |
1 − x ; |
|
|
||||||||||||
|
|
x2 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7.171. y = e2 x−x2 ; |
|
|
|
7.172. y = e− |
x2 |
|
|
|
|
|
|
||||||||||
|
|
|
2 |
; |
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
|
7.174. y = x e x ; |
|
|
|
|
7.175. y = (x − |
2)e |
x ; |
||||||||||||||
|
|
|
|
|
|||||||||||||||||
7.177. y = ln(x + |
|
|
x2 +1); |
7.178. y = x2 ln x; |
|
|
|
||||||||||||||
7.180. y = x −3ln x; |
|
7.181. y = ln(x2 +1); |
|||||||||||||||||||
7.183. y = sin4 x + cos4 x; |
7.184. y = x arctgx; |
|
|
||||||||||||||||||
7.6.Применение производной в задачах
сэкономическим содержанием
Введем обозначения: х – количество произведенной и проданной продукции, R(х) – выручка от реализации этой продукции, С(х) - соответствующие этому выпуску издержки, Р(х) = R(х) – С(х) – полученная при этом прибыль, р(х) – цена единицы продукции. Функцию спроса будем записывать в виде
р = f(х) или x =ϕ( p) .
Предельные издержки обозначаются МС(х) и равны дополнительным издержкам, необходимым для производства одной дополнительной единицы продукции, т.е.
289

MC(x) = C(x) = C(x +1) −C(x) ≈ dC = C′(x) .
В связи с этим будем считать, что MC(x) = C′(x) , т.е. предельные из-
держки равны производной от функции издержек.
Аналогичным образом определяются предельные прибыль P′(x) и вы-
ручка R′(x) , которые определяют, соответственно, прибыль и выручку от про-
изводства и продажи одной дополнительной единицы продукции.
Если прибыль при некотором значении x0 максимальна, то P′(x0 ) = R′(x0 ) −C′(x0 ) = 0 , откуда следует, что R′(x0 ) = C′(x0 ) . Таким образом максимум прибыли достигается при количестве x0 произведенной продукции,
для которого предельная выручка равна предельным издержкам.
|
Эластичностью функции |
y = f (x) называется предел отношения относи- |
|||||||
тельного приращения функции |
y |
к относительному приращению аргумента |
|||||||
|
|
y |
|
|
|
|
|
|
|
x |
при x → 0 , т.е. |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
Ey (x) = lim |
y : |
x |
= lim |
x |
|
y = |
x |
dy . |
|
x |
|
|
||||||
|
x→0 |
y |
x→0 |
y x y dx |
|||||
Эластичность функции в точке х показывает, на сколько процентов изменится значение функции при изменении аргумента на 1%. Функция эластична в точке х, если Ey (x) >1 и неэластична, если Ey (x) <1.
Пример 7.13. Функция спроса на некоторый продукт задана уравнением p =  400 − x , 0 ≤ x ≤ 400 . На сколько изменится выручка, если объем продаж увеличится с 256 до 257 единиц? Сравнить эту величину с предельной выручкой.
400 − x , 0 ≤ x ≤ 400 . На сколько изменится выручка, если объем продаж увеличится с 256 до 257 единиц? Сравнить эту величину с предельной выручкой.
Р е ш е н и е. Выручка R(x) = xp = x 400 − x.
400 − x.
290
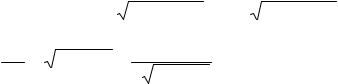
R = R(257) − R(256) = 257 |
400 − 252 − 256 400 − 256 ≈1,27. |
Предельная |
вы- |
|||||||
ручка равна dR = |
400 − x − |
x |
. При х = 256 получим |
|
|
|
||||
dx |
|
2 400 − x |
|
|
|
|
|
|||
dR(256) ≈1,33 . Сравнивая |
R и |
dR , получим |
|
R − dR |
|
|
||||
|
= 0,06. |
|
||||||||
dx |
|
|
dx |
|
dx |
|
|
|
|
|
Пример 7.14. Предприятие быстрого питания выпекает пирожки. |
Вы- |
|||||||||
ручка от продажи |
х – пирожков за неделю равна |
R(x) = |
1 |
|
(60000x − x2 ) , а |
|||||
20000 |
||||||||||
|
|
|
|
|
|
|
|
|||
издержки составляют C(x) = 5000 + 0,56x, 0 ≤ x ≤ 56000 . Сколько пирожков в неделю необходимо выпекать, чтобы прибыль была максимальной? Вычислить прибыль при х = 20000, х = 30000, х = 40000 и сравнить с максимальной.
Р е ш е н и е.
|
P = R |
−C; |
dP |
= dR |
− dC |
= 3 − |
|
x |
|
− 0,56 = 2,44 − |
|
x |
= 0, |
|
|||||||
dx |
10000 |
10000 |
|
||||||||||||||||||
|
|
|
|
|
dx |
dx |
|
|
|
|
|
|
|
|
|
||||||
откуда |
х = 24400. Так как |
d 2 p |
(24400) = − |
|
1 |
|
< 0 , заключаем, что точка х = |
||||||||||||||
dx2 |
|
10000 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
24400 |
является точкой максимума прибыли |
Р. Прибыль при этом составит |
|||||||||||||||||||
24768. При |
х = 20000 прибыль равна 23800, |
|
при х = 30000 прибыль равна |
||||||||||||||||||
23200, а при х = 40000 прибыль равна 12600. |
|
|
|
|
|
|
|||||||||||||||
|
|
|
Пример 7.15. |
Издержки компании в евро при производстве |
х единиц |
||||||||||||||||
продукции заданы функцией |
C(x) = 800 + 0,4x + 0,0002x2 . При каком объеме |
||||||||||||||||||||
производства х |
средние издержки будут наименьшими. |
|
|
||||||||||||||||||
|
|
|
Р е ш е н и е. |
Средние издержки |
|
(x) находятся, как полные издержки |
|||||||||||||||
C |
|||||||||||||||||||||
|
C(x) , отнесенные к объему х произведенной продукции, т.е. |
|
|||||||||||||||||||
|
|
(x) = |
C(x) |
= 800 + 0,4 + 0,0002x . |
Исследуем |
эту |
|
функцию на |
экстремум. |
||||||||||||
|
C |
|
|||||||||||||||||||
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dc |
= − |
800 + 0,0002 = 0, x2 = 4 106 |
, x = 2000. |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
dx |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
291
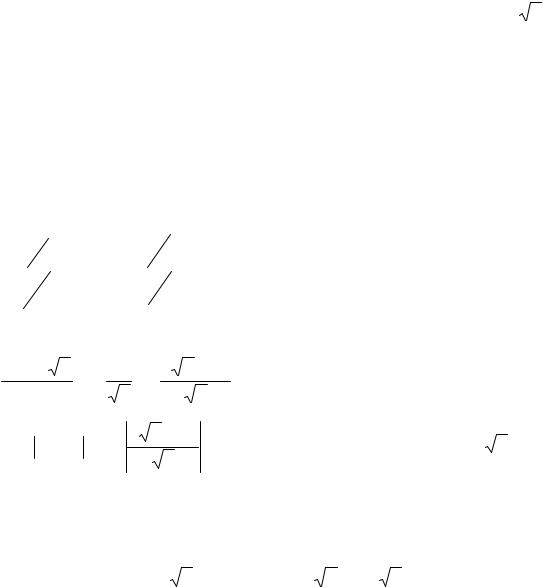
Так как |
d 2c |
(2000) = |
1600 |
> 0, заключаем, что при х = 2000 средние |
||
dx2 |
(2000)3 |
|||||
|
|
|
|
|||
издержки будут наименьшими и составят 1,2 евро на единицу продукции. |
||||||
Пример |
7.16. |
Функция |
спроса задана уравнением p = 30 − 2 x , |
|||
0 ≤ x ≤196 . |
|
|
|
|
|
|
а) Найти интервалы, на которых спрос эластичен, неэластичен и точку, в которой он имеет единичную эластичность.
б) Найти промежутки, на которых выручка R возрастает и убывает сопоставить
|
результаты с результатами пункта а). |
|
|
|
|
|
|||||||||||||||||||||||||
|
Р е ш е н и е. Ценовая эластичность спроса |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
x x |
|
|
|
|
|
p |
dx |
|
|
|
p |
x |
|
|
|
|
|
|
|
|
|
||||
Ex ( p) = lim |
|
|
|
|
= |
|
= |
|
|
|
; |
(будем |
рассматривать |
эластичность, как |
|||||||||||||||||
|
|
p |
|
|
|
|
|
dp |
|
|
|||||||||||||||||||||
|
p→0 |
|
|
|
|
|
x |
dp |
|
|
dx |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
функцию от х). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
а) |
Ex ( p) = |
30 − 2 x |
|
− |
1 |
= |
2 |
x |
−30 |
. |
Спрос |
имеет единичную эластич- |
|||||||||||||||||||
|
|
|
x |
|
|
|
|
|
: |
|
|
|
|
|
|
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||
|
ность, если |
Ex ( p) =1; |
|
2 |
x −30 |
=1, так как 0 ≤ x ≤196 , получим |
x =10, |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x =100 . |
|
|
|
При |
|
|
x <100, |
|
Ex ( p) |
|
>1, |
т.е. |
спрос |
эластичен; |
при |
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
x >100, |
|
Ex ( p) |
|
<1, т.е. спрос неэластичен. |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
б) Выручка |
|
R(x) = xp = 30x − 2x |
x. |
|
|
′ |
|
= 30 −3 |
x = 0, |
x =10, x =100. При |
|||||||||||||||||||||
|
|
|
R (x) |
||||||||||||||||||||||||||||
|
x <100, |
|
|
|
′ |
|
|
> 0 , |
|
|
|
следовательно, |
выручка |
возрастает. |
При |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
R (x) |
|
|
|
|
||||||||||||||||||||||||
|
x >100, |
|
|
′ |
|
|
< 0 |
она убывает. Точка |
x =100 |
является точкой максимума |
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
R (x) |
|
||||||||||||||||||||||||||||
выручки. Таким образом, в области, в которой спрос эластичен увеличение объема производства ведет к увеличению выручки, а в области, где он не-
эластичен, наоборот, к ее снижению.
292
Пример 7.17. Найти эластичность функции y = |
20 + x |
в точке x =10 . |
|
10 + 2x |
|||
|
|
На сколько процентов изменится значение функции в этой точке, если аргумент
увеличить: а) на 1%; б) на 4% ? |
|
|
|
|
|||||
Р е ш е н и е. Найдем эластичность функции |
|
|
|||||||
Ey (x) = |
x |
dy = |
x(10 + 2x) |
|
−30 |
= |
−30x |
; Ey (10) = − |
1 . |
y |
|
(10 + 2x)2 |
(20 + x)(10 + 2x) |
||||||
|
dx |
(20 + x) |
|
|
3 |
||||
Следовательно, если значение аргумента увеличится на 1%, то значение функ-
ции уменьшится на 13 %; если значение аргумента увеличится на 4%, то значе-
ние функции уменьшится на − 34 %.
Задачи для самостоятельного решения
Найти объем продукции х, |
при котором выручка R будет наибольшей. |
|||||
7.185. R = 800x − 0,2x2 ; |
7.186. |
R = 48x2 − 0,02x3 ; |
||||
7.187. R = 400x − x2 ; |
|
2 |
|
|
|
|
7.188. |
R = 30x |
3 |
− 2x. |
|||
Найти объем продукции х, |
при котором средние издержки |
|
на едини- |
|||
C |
||||||
цу продукции наименьшие. |
|
|
|
|
|
|
7.189. C =1,25x2 + 25x +500; |
7.190. C = 0,001x3 +5x + 250; |
|||||
7.191. C = 2x2 + 255x +80000; |
7.192. C = 0,002x3 +55x + 4000; |
|||||
7.193. Функция спроса для некоторого товара имеет вид
p =1000 − 0,5x2 , где х – количество единиц произведенного и проданного то-
вара, р – цена одной единицы при данном уровне производства х. Общие из-
держки заданы функцией C(x) = 400x +1000 . При каком объеме выпуска про-
дукции прибыль будет максимальной? Какова при этом цена одного изделия и средние издержки?
293
7.194. Компания производит игрушки. Выручка и издержки заданы
соответственно функциями R(x) = 500x − x2 , C(x) = 75000 + 2x , где х – число
20
игрушек, произведенных за неделю. При каком объеме выпуска продукции прибыль будет наибольшей?
7.195. |
Функция спроса для некоторого товара имеет вид |
p = |
50 |
, |
|
|
|
x |
|
0 ≤ x ≤ 8000 , где |
р – цена единицы товара, х – количество товара, а издержки |
|||
равны C(x) = 0,5x +500 . Найти: а) максимальную прибыль; б) предельную прибыль в точках х = 900, х = 1600, х = 2500, х = 3600.
7.196. Выручка от сдачи в аренду х единиц площади определяется
функцией R(x) = 2x(900 +32x − x2 ) . Найти: а) дополнительный доход при
увеличении арендуемой площади с 14 до 15 единиц; б) предельный доход при х = 14. Сравнить результаты пунктов а) и б).
Найти ценовую эластичность спроса в указанной точке и установить, будет ли спрос в этой точке эластичным, неэластичным или же он равен единице.
7.197. |
p = 400 −5x, x = 20; |
7.198. |
p = 20 −0,0002x, |
x = 30; |
|||
7.199. |
p = |
500 |
, |
x = 20; |
7.200. |
p = 100 + 2, |
x =10; |
|
|||||||
|
|
x + 3 |
|
|
x2 |
|
|
7.201. |
p =100 − |
0,2x, x =125. |
|
|
|
||
7.202. Функция спроса имеет вид |
x = p2 − 20 p +120 . Найти, на сколько про- |
||||||
|
центов изменится спрос, если цена, равная 2 $, увеличится а) на 1%; б) |
||||||
|
на 5%. |
|
|
|
|
||
Найти эластичность функций в указанных точках.
7.203. |
y = 3x5 +12, x =1, x = 2; |
7.204. |
y = |
2 + 3x |
, |
x =1, x = 2; |
|
5x + 5 |
|||||||
|
|
|
|
|
|
||
7.205. |
y = 3e2 x , x = 0, x =1; |
7.206. |
y = 5 x, |
|
x =1, x = 4; |
||
294
