
- •Раздел I. Элементы линейной и векторной алгебры Основы аналитической геометрии
- •Глава 1. Элементы линейной алгебры
- •1.1. Матрицы и операции над ними
- •1.3. Обратная матрица. Решение матричных уравнений
- •1.4. Ранг матрицы
- •1.6. Система линейных однородных уравнений. Фундаментальная система решений
- •1.7. Контрольные задания к главе 1
- •Глава 2. Элементы векторной алгебры
- •2.1. Векторы на плоскости и в пространстве
- •2.2. Проекция вектора на ось. Скалярное произведение векторов
- •2.3. Векторное и смешанное произведения векторов
- •2.5. Задачи с экономическим содержанием к главам 1, 2
- •2.6. Контрольные задания к главе 2
- •Глава 3. Основы аналитической геометрии
- •3.1. Простейшие задачи аналитической геометрии на плоскости
- •3.2. Прямая линия на плоскости
- •3.4. Прямая и плоскость в пространстве
- •3.5. Понятие гиперплоскости. Выпуклые множества
- •3.6. Контрольные задания к главе 3
- •Раздел II. Введение в математический анализ
- •Глава 4. Функция одной переменной
- •4.1. Функциональная зависимость и способы ее представления
- •4.2. Элементарные функции. Преобразование графиков функций
- •Глава 5. Пределы и непрерывность
- •5.1. Числовая последовательность
- •5.2. Предел последовательности
- •5.3. Предел функции. Раскрытие простейших неопределенностей
- •5.4. Замечательные пределы
- •5.5. Сравнение бесконечно малых
- •5.6. Односторонние пределы
- •5.7. Непрерывность и точки разрыва функции
- •5.8. Контрольные задания к разделу II
- •Глава 6. Производная и дифференциал
- •6.1. Определение производной. Правила дифференцирования
- •6.2. Производная сложной функции
- •6.3 Логарифмическая производная и производная неявной функции
- •6.4. Геометрический и механический смысл производной. Производные высших порядков
- •6.6. Контрольные задания к главе 6
- •Глава 7. Приложения производной
- •7.1. Теорема о среднем значении. Формула Тейлора
- •7.2. Правило Лопиталя-Бернулли
- •7.4. Выпуклость (вогнутость) графика функции. Точки перегиба
- •7.5. Асимптоты. Построение графиков функций
- •7.7. Контрольные задания к главе 7
- •Примерные варианты тестовых заданий
- •ОТВЕТЫ
- •Глава 1
- •Глава 2
- •Глава 3
- •Глава 4
- •Глава 5
- •Глава 6
- •Глава 7
- •Содержание

5.33. lim n +1 n . n→∞ n −1
5.35. lim n −1 n+2 . n→∞ n +3
5.34. lim 2n +3 n+1 . n→∞ 2n +1
n2 −1 n4
5.36.limn→∞ n2 .
5.3. Предел функции. Раскрытие простейших неопределенностей
Определение предела функции в точке. Пусть функция y = f (x) опреде-
лена в некоторой ε - окрестности точки x0 , кроме, быть может, самой точки x0
(в этом случае говорят, что функция определена в проколотой ε - окрестности точки x0 ).
Первое определение предела функции (по Коши, или «на языке ε −δ »):
Число A называется пределом функции f (x) , при x → x0 (или в точке x0 ),
если для любого сколь угодно малого положительного числа ε найдется такое число δ > 0 (вообще говоря, зависящее от ε ), что для всех x , таких, что x − x0 <δ , x ≠ x0 выполнено неравенство f (x) − A <ε .
Обозначается это так: lim f (x) = A или f (x) → A при x → x0 .
x→x0
Первое определение предела функции равносильно второму определению
(по Гейне или «на языке последовательностей»):
Число A называется пределом функции f (x) , при x → x0 (или в точке x0 ),
если для всякой последовательности {xn} значений аргумента, стремящейся к x0 и такой, что xn ≠ x0 для любого n , соответствующая последовательность значений функции {f (xn )} сходится к A .
Пример 5.8. 1) Доказать, пользуясь определением по Коши, что число A = 7 является пределом функции y = 2x +1 при x →3;
2) Доказать, пользуясь определением по Гейне, что число A = 3 является
пределом функции f (x) = |
x2 |
− x − 2 |
при x → 2 . |
|
x − 2 |
||
|
|
|
216
|
|
Решение: 1) Рассмотрим произвольное ε > 0 . Требуется найти для него |
||||||||||||||||||||||||||||||||||||||||||||||||
такое число δ > 0 , что для всех x , таких, что |
|
|
x − 3 |
|
<δ , |
x ≠ 3 , было бы выпол- |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
нено неравенство |
|
|
f (x) − 7 |
|
= |
|
2x +1 − 7 |
|
|
|
<ε . |
|
|
|
|
|
2x − 6 |
|
|
|
|
|
|
|
x − 3 |
|
< ε |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Последнее неравенство приводится к виду |
|
|
|
<ε или |
|
|
. Таким |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
образом, |
если принять δ = ε , то выполнены все условия определения предела |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
по Коши. Это и значит, что lim(2x +1) = 7 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2) Пусть {x } |
– произвольная последовательность, такая, что lim x = 2 |
и |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
n |
|
|
|||
x ≠ 2 |
для любого |
n . Тогда lim f (x |
) = lim |
|
x 2 − x |
− 2 |
|
|
= lim |
|
(x |
|
+1)(x − 2) |
. |
|
|||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
n |
|
|
|
|
n→∞ |
|
xn − 2 |
|
|
|
|
n→∞ |
|
|
|
xn − 2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Далее, |
т.к. xn ≠ 2 , |
xn − 2 ≠ 0 , то мы имеем право сократить дробь на |
xn − 2 : |
|||||||||||||||||||||||||||||||||||||||||||||||
lim |
(xn |
+1)(xn − 2) |
= lim(x |
n |
+1) = lim x +1 = 2 +1 = 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
n→∞ |
|
xn − 2 |
|
|
|
|
n→∞ |
|
|
|
|
n→∞ |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Согласно |
определению |
|
предела |
функции |
|
по |
Гейне |
это |
|
и |
значит, что |
|||||||||||||||||||||||||||||||||||||||
lim |
|
x2 |
− x − 2 |
= 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x − |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x→2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Пример 5.9. Доказать, что функция |
f (x) |
= sin |
1 |
|
|
не имеет предела в точке |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Решение: Воспользуемся |
определением предела функции в точке по |
|||||||||||||||||||||||||||||||||||||||||||||||
Гейне. |
Рассмотрим последовательность |
|
x ′ |
= |
|
|
1 |
|
|
|
|
. |
Тогда |
lim x ′ = 0 |
и |
|||||||||||||||||||||||||||||||||||
|
π + 2πn |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n→∞ n |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn′ ≠ 0 |
для всякого n N . При этом lim f (xn′) = limsin(π |
+ 2πn) = lim1 =1. Если |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
n→∞ |
|
|
2 |
|
|
|
|
|
n→∞ |
|
|
|
|||||||||||
же выбрать последовательность |
x ′′ = |
|
|
|
|
|
1 |
|
|
|
|
|
|
( x |
|
′′ |
≠ 0 для всех n N ), кото- |
|||||||||||||||||||||||||||||||||
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
+ 2πn |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
рая также является бесконечно малой, то
217

|
′′ |
3π |
+ 2πn) = lim(−1) = −1. |
|
|
|
|
|
|
|
|||
lim f (xn ) = limsin( |
2 |
|
|
|||
n→∞ |
n→∞ |
|
n→∞ |
|
|
|
Таким образом, мы нашли две различные последовательности {x′ |
} |
и {x′′}, |
||||
|
|
|
|
n |
|
n |
сходящиеся к числу x0 |
= 0, для которых соответствующие последовательности |
|||||
′ |
′′ |
сходятся к различным числам. Это вступает в противоречие |
||||
{f (xn )} |
и {f (xn )} |
|||||
со вторым определение предела функции, следовательно, функция f (x) = sin 1 |
|||||||
|
|
|
|
|
|
|
x |
не имеет предела в точке x0 |
= 0. |
|
|
|
|
|
|
Определение предела |
функции |
на |
бесконечности. Пусть функция |
||||
y = f (x) определена на бесконечном промежутке (a;+∞) . |
|||||||
Число A называется пределом функции f (x) , при x → +∞, если для любого |
|||||||
сколь угодно малого положительного числа |
ε найдется такое число M > 0 , |
||||||
что для всех значений x > M , выполнено неравенство |
|
f (x) − A |
|
<ε . |
|||
|
|
||||||
Обозначается это так: lim f |
(x) = A или |
f (x) → A при x → +∞. |
|||||
x→+∞ |
|
|
|
|
|
|
|
Равносильное определение предела функции на «на языке последовательно-
стей» будет выглядеть так: |
|
|
|
|
Число A называется пределом функции f (x) , |
при x → +∞, если для всякой |
|||
последовательности x такой, что |
lim x |
n |
= +∞, |
соответствующая последова- |
n |
n→∞ |
|
|
|
тельность значений функции f (xn ) |
сходится к A . |
|
||
Аналогично определяется lim f (x) и lim f (x) . |
||||
x→−∞ |
x→∞ |
|
||
Бесконечно малые и бесконечно большие функции. Функция y = f (x) на-
зывается бесконечно большой при x → x0 (в точке x0 ), если для всякого числа
M > 0 найдется такое число δ > 0 , что для всех x , таких, что x − x0 <δ , x ≠ x0
выполнено неравенство |
|
f (x) |
|
> M (или если для всякой последовательности xn |
|||
|
|
||||||
такой, что lim x |
n |
= x , имеет место равенство, lim f (x ) = ∞). |
|||||
n→∞ |
0 |
|
|
|
n→∞ |
n |
|
Функция y = f (x) называется бесконечно малой при x → x0 (в точке x0 ),
если lim f (x) = 0 .
x→x0
218

Пример 5.10. Доказать, что функция |
f (x) = 2−x является бесконечно малой |
|||||||||||
при x → +∞. |
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Требуется доказать, что |
lim 2−x = 0 , т.е. что для любого числа |
|||||||||||
|
x→+∞ |
|
|
|
|
|
|
|
|
|||
ε > 0 существует число M > 0 , такое, что |
|
2−x − 0 |
|
<ε для всех x > M . |
||||||||
|
|
|||||||||||
Рассмотрим любое ε > 0 . Неравенство |
|
2−x |
− 0 |
|
|
<ε |
равносильно неравенству |
|||||
|
|
|||||||||||
2−x <ε и, далее, неравенствам −xln 2 < ln ε , |
x > |
lnε |
|
= ln 2ε . Таким образом, |
||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
−ln 2 |
||
для всякого ε > 0 найдено число M = ln 2ε из определения предела. Это и озна-
чает, что lim 2−x = 0 .
x→+∞
Свойства бесконечно малых функций.
1)Сумма и произведение любого конечного числа бесконечно малых при
x→ x0 функций есть бесконечно малая при x → x0 функция;
2)Произведение ограниченной функции на бесконечно малую есть бесконечно малая функция;
3)Функция y = f (x) является бесконечно малой при x → x0 тогда и только
тогда, когда y = |
1 |
– бесконечно большая при |
x → x ( 1 |
=∞, |
1 |
= 0 ). |
|
|
|
||||||
|
f (x) |
|
0 |
0 |
|
∞ |
|
|
|
|
|
||||
Операции над пределами функций. |
|
|
|
|
|
||
1) Если lim f (x) = A, |
lim g(x) = B , то |
|
|
|
|
|
|
x→x0 |
|
x→x0 |
|
|
|
|
|
а) lim f (x) ± g(x) = A ± B ;
x→x0
б) lim cf (x) = cAдля любого c R ;
x→x0
в) lim f (x)g(x) = AB ;
x→x0
г) lim f (x) = A , если B ≠ 0 ; x→x0 g(x) B
2) если lim f (x) = A, lim g( y) = B , то lim g( f (x)) = B ; |
||
x→x0 |
y→A |
x→x0 |
219

3) для всех основных элементарных функций в любой точке x0 их области оп- |
||||
ределения имеет место равенство lim f (x) = f (lim x) = f (x0 ) . |
||||
|
x→x0 |
x→x0 |
|
|
Говорят, что отношение двух функций |
f (x) |
при x → x представляет со- |
||
|
|
|||
|
|
g(x) |
0 |
|
|
|
|
||
бой неопределенность вида 0 |
, если lim f (x) = 0 , |
lim g(x) = 0 . Аналогично оп- |
||
0 |
x→x0 |
|
|
x→x0 |
ределяются неопределенности вида |
∞ |
, ∞ − ∞, 0 ∞, |
00 , ∞0 , 1∞ . |
|||||||||
∞ |
||||||||||||
Пример 5.11. Найти следующие пределы: |
|
|
|
|||||||||
1) lim |
3x2 |
− 2 |
|
; |
2) lim |
x2 |
− 9 |
|
; |
|||
5x2 − |
4x +1 |
2x2 − 4x |
− 6 |
|||||||||
x→1 |
|
|
|
x→3 |
|
|||||||
lim
x→1
3) lim |
|
x −1 − 3 |
; |
4) |
lim |
1 − 4x + 4x2 |
; |
|
|
|
|
|
|
|
||||||||||
|
x −10 |
|
|
5x2 +1 |
|
|
|
|
|
|
|
|||||||||||||
|
x→10 |
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
||||||||||
5) |
lim (1 − 4cos x)2−x . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение: |
|
|
|
1) |
Справедлива |
|
цепочка |
|
|
равенств |
||||||||||||||
3x |
2 |
− 2 |
|
|
= |
|
lim(3x2 − 2) |
= |
3(lim x)2 |
− 2 |
|
|
= |
3 − 2 |
|
= |
1 |
. Здесь |
||||||
|
|
|
|
x→1 |
|
x→1 |
|
|
|
|||||||||||||||
5x2 |
− 4x +1 |
lim(5x2 − 4x +1) |
5(lim x)2 − 4lim x +1 |
5 − 4 +1 |
2 |
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
x→1 |
|
|
x→1 |
x→1 |
|
|
|
|
|
|
|
|
||||
мы воспользовались теоремами об арифметических действиях над пределами и теоремой о пределе элементарной функции.
2) Поскольку пределы числителя и знаменателя равны нулю, мы имеем де-
ло с неопределенностью вида |
0 |
. «Раскроем» эту неопределенность, т.е. изба- |
||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
вимся от нее, |
разложив числитель и знаменатель на множители и сократив |
|||||||||||
дробь |
на |
|
x − |
3 : |
lim |
x2 − 9 |
= lim |
(x − 3)(x + 3) |
|
|||
|
2x2 − 4x − 6 |
2(x − 3)(x +1) |
||||||||||
|
|
|
|
|
|
|
|
x→3 |
x→3 |
|||
= lim |
x + 3 |
= |
3 + 3 |
= 6 = |
3 . |
|
|
|
|
|
|
|
|
2(3 +1) |
|
|
|
|
|
|
|
||||
x→3 |
2(x +1) |
8 |
4 |
|
|
|
|
|
|
|
||
3) Снова имеем неопределенность вида 00 . Для ее раскрытия умножим числитель и знаменатель дроби на выражение, сопряженное к числителю и вос-
220

пользуемся |
|
|
формулой |
разности |
квадратов: |
|||
lim |
|
x −1 − 3 |
= lim |
( x −1 − 3)( x −1 + 3) |
= lim |
x −1 − 9 |
|
|
|
x −10 |
x −10( x −1 + 3) |
x −10( x −1 + 3) |
|||||
x→10 |
x→10 |
x→10 |
||||||
= lim |
1 |
|
= |
1 . |
|
|
|
|
|
|
|
|
|
||||
x→10 |
( x −1 + 3) |
6 |
|
|
|
|||
4) Числитель и знаменатель дроби представляют собой бесконечно большие при x → +∞ функции, поэтому здесь имеет место неопределенность вида
∞ . Поступая как при вычислении предела последовательности, разделим чис- |
||||||||||||||||
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
литель |
и |
знаменатель |
дроби |
на |
старшую |
степень |
x : |
|||||||||
|
|
|
|
|
1 |
|
4 |
+ 4 |
|
|
|
|
|
|||
|
1 − 4x + 4x2 |
= lim |
|
− |
|
|
= 4 . |
|
|
|
|
|||||
lim |
|
x2 |
|
x |
|
|
|
|
||||||||
5x2 |
+1 |
|
|
|
1 |
|
|
|
|
|
||||||
x→+∞ |
x→+∞ |
5 |
|
5 |
|
|
|
|
||||||||
|
|
|
|
|
+ |
|
|
|
|
|
|
|
||||
|
|
|
|
|
x2 |
|
|
|
|
|
||||||
|
5) Справедливо неравенство −3 <1 |
− 4cos x < 5 , т.е. функция y =1 − 4cos x |
||||||||||||||
является ограниченной на всей числовой оси, а потому при ее умножении на бесконечно малую при x → +∞ функцию y = 2−x получим также бесконечно
малую при x → +∞ функцию. Таким образом, lim (1 − 4cos x)2−x = 0 .
x→+∞
Пределы функций и неравенства.
1) Если lim f (x) = A, lim g(x) = B , и f (x) ≤ g(x) для всех x из некоторой
x→x0 x→x0
проколотой ε - окрестности точки x0 , то A ≤ B ;
2) Если предел функции в данной точке положителен (отрицателен), то и все значения указанной функции положительны (отрицательны) в некоторой проколотой окрестности этой точки (обратное, вообще говоря, неверно: напри-
мер, пределом последовательности с положительными членами xn = 1n является
число ноль);
3) (теорема о промежуточной переменной) Пусть функции f (x) , f1 (x) , f2 (x) определены в некоторой проколотой ε - окрестности точки x0 и
221

f1 (x) ≤ f (x) ≤ f2 (x) |
для всех из этой окрестности. Пусть также |
|
lim f1 |
(x) = lim f2 (x) = A. Тогда lim f (x) также существует и равен A . |
|
x→x0 |
x→x0 |
x→x0 |
3) Если функция имеет предел в данной точке, то она ограничена в некоторой окрестности этой точки.
Задачи для самостоятельного решения
5.37. Пользуясь первым определением предела (по Коши), доказать, что.
а) lim 3x + 2 = −1; |
б); lim 2 − x =1; |
||||
x→−1 |
|
|
|
|
x→1 |
в) lim |
1 |
= |
1 |
; |
г) lim = x2 = 4 . |
x→3 |
x |
|
3 |
|
x→2 |
5.38. Пользуясь вторым определением предела (по Гейне), доказать, что.
а) |
lim (x2 − x) = 6 ; |
б) lim x2 −3x + 6 = 4; |
|
|
||||||
|
x→−2 |
|
|
|
|
|
x→2 |
|
|
|
в) |
lim 1 − x2 |
= |
|
3 |
; |
г) lim =(x + 2a)5 = 243a5 . |
|
|||
|
2 |
|
||||||||
|
1 |
|
|
|
|
x→a |
|
|
|
|
|
x→2 |
|
|
|
|
|
|
|
|
|
5.39. Доказать, что функция y = f (x) не имеет предела в точке x = x0 . |
|
|||||||||
а) |
f (x) = cos x , |
x = +∞; |
б) |
f (x) = tgx , x |
= π |
; |
|
|||
|
|
|
|
0 |
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
в) |
f (x) = sign x , |
x0 = 0 ; |
|
|
|
|
|
|||
г) |
|
если x − рациональное |
(функция Дирихле), x0 = |
1 . |
||||||
f (x) = 1, |
||||||||||
|
0, |
если x − иррациональное |
|
|
|
2 |
||||
5.40. Доказать, что функция y = f (x) является бесконечно малой при x → +∞.
а) |
f (x) = sin x |
; |
|
б) |
f (x) = |
1 |
+ |
1 |
; |
|
|
|
|
x |
2x |
|
|
||||||||
|
|
x |
|
|
|
|
|
|
|
|
||
в) |
f (x) = |
cos3 |
x |
; |
г) |
f (x) = |
(cos x +sin x)e |
−x |
. |
|||
x +1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Найти пределы:
222
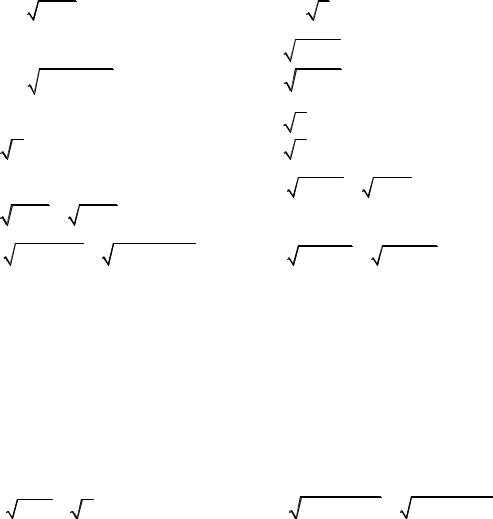
5.41. lim |
x2 −5x + 6 |
. |
|
|
|
|
|
|
5.42. lim |
|
|
x2 |
−6x +8 |
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
x2 −9 |
|
|
|
|
|
|
|
|
|
x2 |
−8x +12 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
x→3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
5.43. lim |
1 − x2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.44. lim |
a2 − x2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 − x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a3 + x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→−a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
5.45. lim |
|
|
3t2 −t − 2 |
|
. |
|
|
|
|
|
|
5.46. lim |
x3 |
−6x2 +11x −6 |
|
. |
|
|
||||||||||||||||||||||||||||
2t2 +5t −7 |
|
|
|
|
|
|
|
|
|
|
|
x2 −3x + 2 |
|
|
|
|
|
|||||||||||||||||||||||||||||
t→1 |
|
|
|
|
|
|
|
|
x→1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
5.47. lim |
|
|
2 y |
2 +5y + 2 |
|
|
|
. |
5.48. lim |
|
|
|
|
cos 2ϕ |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
+ 7 y2 + 6 y |
sinϕ −cosϕ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
y→−2 2 y3 |
|
x→π |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.49. lim |
1 −32α . |
|
|
|
|
|
|
|
|
|
|
|
5.50. lim |
x5 −1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
α→0 |
|
3α −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→1 |
x4 −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5.51. lim |
|
1 |
|
|
|
− |
|
|
|
|
6 |
|
|
|
|
5.52. lim |
|
|
1 |
|
|
− |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||||||
|
|
3 |
|
|
x |
2 |
|
− |
|
|
|
|
|
|
1 |
− x |
3 |
|
|
|
|
|
|
|||||||||||||||||||||||
x→3 |
x − |
|
|
|
|
|
|
|
9 |
|
x→3 |
1 − x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
5.53. lim |
|
|
|
|
|
x |
|
|
|
|
|
|
. |
|
|
|
|
|
|
5.54. lim |
1 − x2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 − |
|
x + 4 |
|
|
|
|
|
|
1 − |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x→0 |
|
|
|
|
|
|
|
|
|
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
5.55. lim |
|
|
|
|
p +1 |
|
|
|
|
|
. |
5.56. lim |
|
|
|
x2 + 4 − 2 |
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 +9 −3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
p→−11 |
1 + p + p2 |
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
5.57. lim |
|
|
|
x −8 |
. |
|
|
|
|
|
|
|
|
|
|
|
5.58. lim |
|
|
|
x −1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x→8 |
3 |
|
x − 2 |
|
|
|
|
|
|
|
|
|
|
|
x→1 |
3 |
x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5.59. lim |
|
|
|
|
x2 + x −12 |
|
|
|
|
|
. |
5.60. lim |
|
|
|
x +10 − 4 − x |
. |
|
|
|||||||||||||||||||||||||||
|
|
|
|
x − 2 − |
|
|
|
4 − x |
|
|
|
|
2x2 − x − 21 |
|
|
|
||||||||||||||||||||||||||||||
x→3 |
|
|
|
|
|
|
|
|
x→−3 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
5.61. lim |
|
|
|
|
1 + x + x − 7 + 2x − x2 |
. 5.62. lim |
|
|
|
3x +17 − 2x +12 |
. |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 − 2x |
|
|
|
|
x2 + |
8x +15 |
|
|
|
|
||||||||||||||||||||||||
x→−3 |
|
|
|
|
|
|
|
|
x→−5 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
5.63. lim |
|
|
|
|
(x −1)2 |
|
|
. |
|
|
|
|
|
|
5.64. lim |
|
|
|
|
x − 2 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
2x2 − x −1 |
|
|
|
|
|
|
|
|
|
|
−3x + |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
x→∞ |
|
|
|
|
|
|
|
|
x→∞ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
5.65. lim |
x4 − 2x −1001 |
. |
|
|
|
5.66. lim |
|
|
3x2 − 2x3 − x +1 |
|
. |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
3x4 − x2 −1 |
|
|
|
|
|
4x3 +3x2 + 7x − |
4 |
|
|
||||||||||||||||||||||||||||||||||
x→∞ |
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|||||||||||||||||||||||||||||||||
5.67. lim |
2x4 +3x2 +5x −6 |
5.68. lim |
|
|
|
(2x3 + 4x +5)(x2 + x +1) |
. |
|||||||||||||||||||||||||||||||||||||||
|
|
x3 +3x2 + 7x −1 |
(x |
+ 2)(x4 + 2x3 + |
7x2 + x −1) |
|||||||||||||||||||||||||||||||||||||||||
x→∞ |
|
|
x→∞ |
|
||||||||||||||||||||||||||||||||||||||||||
5.69. limx→∞(3 |
x +1 − 3 |
|
x ). |
|
|
|
|
5.70. limx→∞( |
|
|
x2 + ax +b − |
|
x2 + cx + d ) |
|
||||||||||||||||||||||||||||||||
223
