3.312. Составить уравнение плоскости, проходящей через точку М1(2; –2; 1) и

лежат в одной плоскости, и составить уравнение этой плоскости.

3.314. Составить уравнение плоскости, проходящей через две параллельные

3.315. Найти проекцию точки С(3; –4; –2) на плоскость, проходящую через па-

3.5. Понятие гиперплоскости. Выпуклые множества

Обобщением понятия плоскости трехмерного пространства на случай n −мерного пространства является понятие гиперплоскости. Каждую гиперплоскость можно задать одним линейным уравнением вида:

176

где a1,a2 ,..., an ,b –действительные числа, a12 +a22 +... + an2 ≠ 0 .

Очевидно, что на декартовой плоскости ( n = 2 ) уравнение (0.69) описывает прямую. Если в n −мерном пространстве задана гиперплоскость (0.69), то этой гиперплоскостью все точки пространства разбиваются на два полупро-

странства:

Эти полупространства пересекаются по самой гиперплоскости (0.69). Множество Χ точек n −мерного пространства называется выпуклым, если

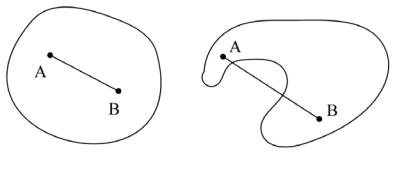
для любых A, B X справедливо λA + (1 − λ)B X , λ [0,1] , т.е. выпуклое множество наряду с любыми двумя своими точками A и B содержит и все точки отрезка AB . Например, на рисунке 3.21 первое множество является выпуклым, а второе–нет.

Рис 3.21.

Пересечение любой совокупности выпуклых множеств есть выпуклое множество.

Каждое полупространство (0.70), (0.71) является выпуклым множеством. Гиперплоскость (0.69), как пересечение выпуклых множеств есть выпуклое множество.

Через каждую точку границы выпуклого множества на плоскости проходит, по крайней мере, одна опорная прямая, имеющая общую точку с границей, но не рассекающая это множество.

177

В трехмерном пространстве через каждую точку границы выпуклого множества проходит хотя бы одна опорная плоскость, оставляющая это множество в одном полупространстве.

Множество Χ точек n −мерного пространства называется ограниченным,

Все знаки неравенств одного смысла могут быть достигнуты умножением, в случае необходимости, обеих частей неравенства на -1. Пересечение этих полупространств, называемое выпуклой многогранной областью, определяет множество решений системы линейных неравенств (0.72). Если это пересечение ограничено, оно называется выпуклым многогранником n −мерного простран-

ства \n . Таким образом, множество решений системы линейных неравенств (0.72) представляет собой либо выпуклый многогранник, либо выпуклую неограниченную область, либо пустое множество точек.

Частным случаем, но крайне важным с точки зрения графической иллюстрации решения, является система m линейных неравенств с двумя переменными, имеющая вид:

где a11, a12 ,...,am1, am2 ,..., b1,...,bm − заданные действительные числа.

Системы вида (0.73) возникают при моделировании многих экономических задач.

178

Так как (0.73) – совокупность линейных неравенств, необходимо определить понятие решения линейного относительно переменных x1 и x2 неравенст-

ва:

как координаты точек пространства \2 , т.е. плоскости x1O x2 , то областью ре-

шений неравенства называется совокупность всех точек плоскости, координаты которых удовлетворяют неравенству (0.74). Областью решений линейного неравенства является одна из полуплоскостей, на которые граничная прямая a1x1 + a2 x2 = b делит плоскость x1O x2 .

Одной из экономических интерпретацией неравенства (0.74) является бюджетное множество, которое определяется как множество наборов товаров

(x1, x2 ) в количествах x1 и x2 соответственно (первого и второго вида), кото-

рые можно приобрести по ценам a1 и a2 за единицу товара, имея заданную сумму b денежных единиц.

строим по двум точкам, а именно, точкам пересечения с осями координат. Построим прямую (l1 ): 3x1 + 2x2 = 6 . Если x2 = 0 , то 3x1 + 2 0 = 6 , x1 = 2 , значит,

прямая (l1 ) пересекает ось O x1 в точке А (2; 0); если x1 = 0 , то 3 0 + 2x2 = 6 , x2 = 3 , значит, прямая (l1 ) пересекает ось O x2 в точке

179

В (0; 3). Аналогично устанавливаем, что прямая (l2 ) пересекает оси O x1 и O x2

в точках С (1; 0) и D (0; 1) соответственно. Прямые (l3 ) и (l4 ) задают уравне-

ния осей координат O x2 и O x1 соответственно.

Каждая из построенных прямых разбивает плоскость на две полуплоскости, одна из которых (ее направление укажем стрелкой) является решением неравенства, соответствующего граничной прямой. Для того, чтобы узнать, какая именно из двух полуплоскостей является решением неравенства, в неравенство, соответствующее рассматриваемой граничной прямой, подставим координаты точки, не лежащей на этой прямой, например, для (l1 ) и (l2 ) подставим точку

О(0; 0): 3 0 + 2 0 ≤ 6 , (l1 ); 1 0 +1 0 ≤1, (l2 ). Получим числовые неравенства

0 ≤ 6 , которое является истинным, следовательно, стрелка направлена от пря-

мой (l1 ) в полуплоскость с точкой О(0; 0) и 0 ≥1, которое является ложным.

Следовательно, стрелка направлена от прямой (l2 ) в полуплоскость, не содер-

жащую точку О(0; 0). Неравенство x1 ≥ 0 задает полуплоскость, лежащую пра-

вее прямой (l1 ); а неравенство x2 ≥ 0 задает полуплоскость, лежащую выше прямой (l2 ). Пересечение отмеченных полуплоскостей (четырехугольник

АСDВ) и есть область решений изучаемой системы неравенств:

180

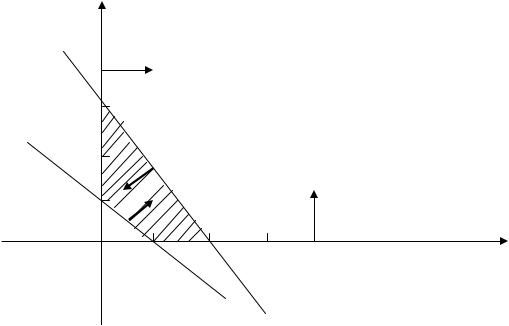
x2

(l3 )

В 3

(l2 ) 2 (l1 )

Рис. 3.22.

Задачи для самостоятельного решения

181