4 Эксперимент: фактор твердость шлифовального круга

(изменяем твердость: СМ-2; СТ-3)

• СОЖ ИЛС – 5 Минеральное масло;

• материал круга Эль бор , марки ЛКВ;

• зернистость (80/63) -ЛКВ;

• связка керамическая

• скорость соответствующая 50 м/с;

• глубина 0, 02мм.;

• подача 2.5 м/мин.;

• геометрия круга 8х9х4 (ширина, наружный диаметр, внутренний диаметр);

• пропитка серой.

11.1.3 Статистическая обработка результатов эксперимента

Однофакторная, линейная по параметрам модель, имеет вид

где _i(X) - известные функции; bi - параметр модели.

Часто применяются функции вида:

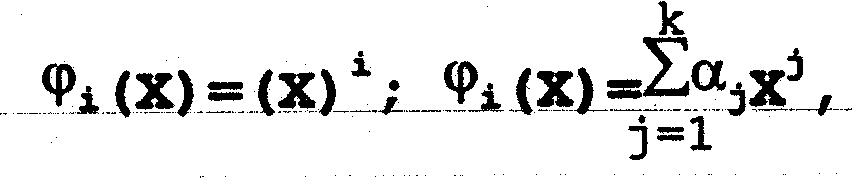
Где  - известный параметр.

Представление моделей в виде обычных многочленов имеет сле­дующие недостатки:

а) с повышением степени многочлена увеличива­ется погрешность оценки его параметров;

б) при необходимости по­высить степень многочлена (например, при уточнении модели) рас­чет значений всех параметров нового многочлена приходится начи­нать с начала.

Этих недостатков лишена модель в виде суммы ортогональных по­линомов Чебышева:

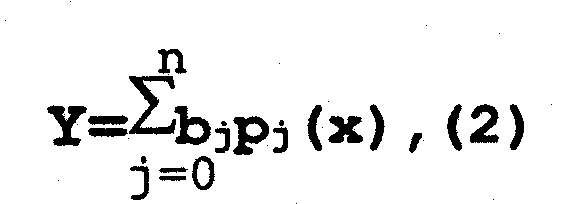
где pj(х) - ортогональные полиномы Чебышева; bj - параметры

модели.

Нет алгоритма априорного выбора числа и расположения уровней фактора, и эта задача решается эвристически в зависимости от трудоемкости и требуемой точности эксперимента.

Рекомендуется расстояние между уровнями факторов, при которых будет производится измерение отклика, брать постоянным. Число уровней лучше выбирать нечетным. Нормализацию фактора следует производить симметрично, согласно формуле:

где xij - нормализованный i-й уровень j-гo фактора;

Xi j - натуральный i-й уровень j-гo фактора;

Xj - постоянный шаг изменения натурального значения j-го фактора;

Xj - средний уровень j-гo фактора.

Следует отметить, что существует два варианта построения опы­та:

1. при проведении эксперимента, на каждом уровне фактора де­лается по m измерений отклика.

2. при проведении эксперимента, на каждом уровне фактора де­лается однократное измерение отклика, а для определения дисперсии воспроизводимости отклика проводится дополни­тельный эксперимент на одном-трех уровнях фактора.

В нашем случае будем пользоваться вторым вариантом, т.к. он позволяет получить математическую модель процесса за меньшее количество опытов.

Последовательность расчета параметров модели.

Пусть было проведено N опытов

u=l; 2; 3; ... ;N, t - фактор, Н - параметр оптимизации.

Предполагается, что модель имеет вид полинома, степень и па­раметры которого следует определить . Для оценки погрешности оп­ределения параметров модели и проверки ее адекватности необходи­мо найти дисперсию воспроизводимости. С этой целью при значениях фактора равных t1, t2, t_N было проведено по пять испытаний.

1 . Определяем нормализованное значение факторов по формуле (3)

2. Вычисляем дисперсии для каждой из этих серий по формуле:

где m - число опытов в серии;

Yi - значение параметра оптимизации в i-ом опыте серии;

Y - среднее значение параметра оптимизации в серии.

Получили , S²i; S²2; S²Ni

3. Оцениваем однородность полученных дисперсий (однородность дисперсий означает то, что они равны дисперсии генераль­ной совокупности)эту оценку производим с помощью крите­рия Кохрена.

Для этого вычисляем наблюдаемое значение критерия Кохрена:

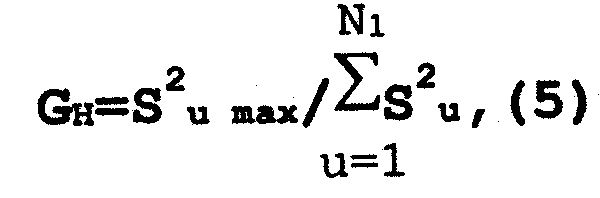
где S²_u max - максимальная оценка дисперсии среди Ni сравнивае­мых дисперсий (все Ni выборок имеют одинаковый объем т) ;

Исходя из выбранной доверительной вероятности, а так же пара­метров Ni=n и m определяем по таблице критическое значение крите­рия Кохрена Gk, должно выполняться неравенство

Gh<Gk

4. Определяем дисперсию воспроизводимости:

где Ni - количество серий опытов по m измерений в каждой .

5. Анализируя результаты эксперимента, делается гипотетический вывод о порядке полинома представляющего собой математическую модель .

В общем виде этот полином представляется в следующем виде;

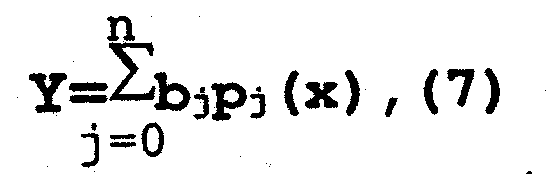
j=0 где pj (х) - ортогональные полиномы Чебышева; bj - параметры

модели .

б . Вычисление параметров модели удобно производить в таблич­ной форме . Значения скорректированных полиномов Р^*j выбира­ются из таблиц

Таблица 3.1

Расчет параметров модели
Т	X	Y	Y2	Р*1	YP* 1	Р*2	YP*2	Р*n	YP*n
Натуральное значение фактора	Нормализо­ванное pначение фактора	Параметр оптимизации
Y1 Итого

При пользовании таблицами:

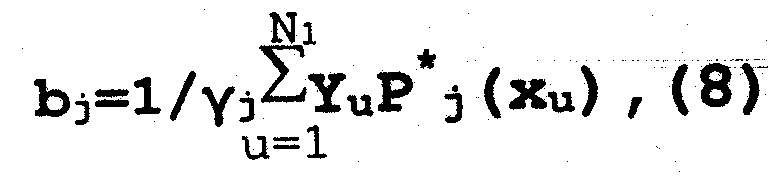
7 . Определяем дисперсию, которая указывает на степень приближения моделью того или иного порядка результатов эксперимента :

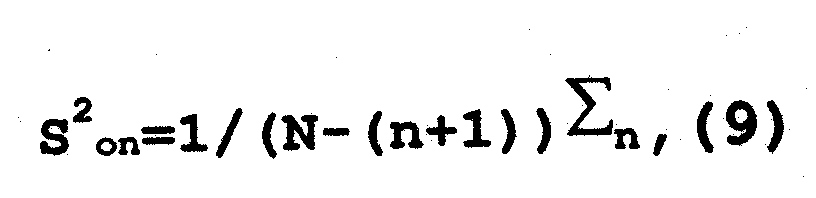
где n - порядок полинома;

N - количество уровней варьирования факторов

причем

_n - определяем по таблице

8 . Для проверки адекватности модели в виде полинома n-ого порядка определяем наблюдаемое значение критерия Фишера:

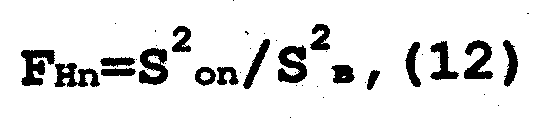
Исходя из доверительной вероятности и величин выборок (S²в вычислено для выборки из m2>Ni*m элементов; S²_оп вычислена для выборки из m1>N элементов) . Если Fh>Fk - то модель не адекватна. Тогда вычисляем ещё один параметр bj соответствующий полиному более высокого порядка. Снова определяем S²o(n+1) и снова производится проверка. Если Fн<Fк ,то модель адекватна.

9. Определяем доверительный интервал оценок параметров модели;

где (bj) - доверительный интервал для параметра bj;

S²_в- дисперсия воспроизводимости;

t(P,m) - критерий Стьюдента.

10. Округляем параметры, с учетом значений доверительных ин­тервалов. Имеем:

Р1(х)…P_n (x) выбираем по таблице.

11. Переходим к натуральной модели, подставляя в полученную нормализованную модель значение нормализованного фактора.