Таким образом, главный момент системы сил относительно второго центра равен главному моменту относительно первого центра плюс момент главного вектора, приложенного к первому центру, относительно второго центра.

Инварианты системы сил

Инвариантами называются векторные или скалярные параметры, которые не зависят от преобразования координат. В системе сил, как мы видим, таким параметром является главный вектор. Его называют векторным инвариантом системы сил. Главный момент инвариантом не является, так как он различен для различных центров приведения. Однако инвариантом служит скалярное произведение главного вектора на главный момент. В самом деле

P MO2 = P (O2O1 ×R)+ P MO1 = P MO1 , P (O2O1 ×P)

Отсюда также вытекает, что инвариантом является и проекция главного момента на направление главного вектора

Частные случаи приведения системы сил к центру

Исходя из рассмотрения скалярного инварианта, все случаи приведения системы сил можно классифицировать следующим образом:

При равенстве нулю скалярного инварианта:

•Главный вектор не равен нулю ( P ≠ 0 ), а главный момент равен нулю

( MO = 0 ). Система приводится к равнодействующей, равной главному вектору;

56

•Главный вектор равен нулю ( P = 0 ), а главный момент не равен нулю

( MO ≠ 0 ). Система приводится к паре сил с моментом, равным главному моменту системы;

•Главный вектор и главный момент не равны нулю ( P ≠ 0 , MO ≠ 0 ), но угол между ними равен 90D . В этом случае возможно дальнейшее упрощение

Система приводится к равнодействующей силе, но линия её действия от-

стоит от первоначального центра приведения на расстоянии OO1 = d = MPO

• Главный вектор и главный момент равны нулю. Система уравновешена:

R = ∑Fk = 0, MO = ∑MO (Fk )= 0.

В случае, когда скалярный инвариант не равен нулю, полезно рассмотреть следующие варианты приведения сил:

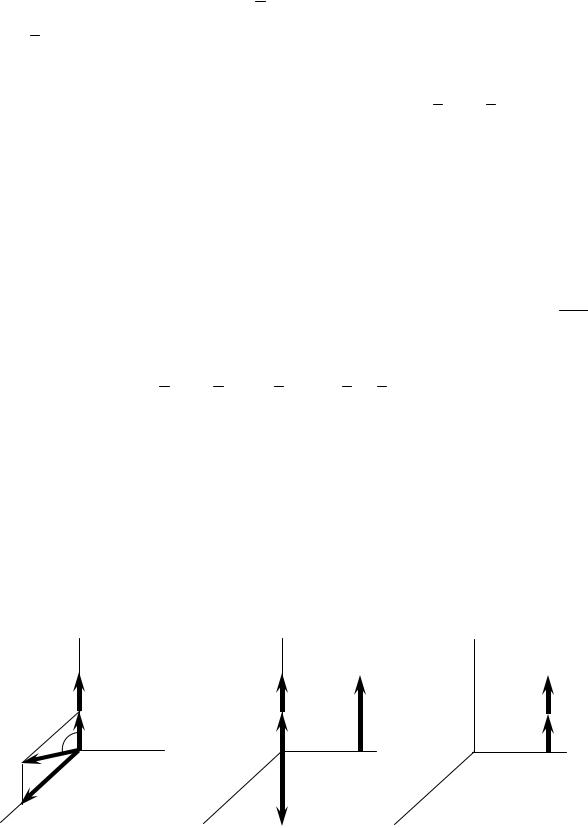
Угол между главным вектором и главным моментом равен 0 или 180°. Такая комбинация главного вектора и главного момента называется динамой или динамическим винтом. Линия, вдоль которой действуют оба вектора называется осью динамы.

Угол между главным вектором и главным моментом произволен. В этом случае возможно упрощение

57