4 Относительная деформация в заданном направлении.
Найдем выражение для величины относительной деформации (213) для элемента длины, ориентированного в некотором заданном направлении. Поскольку тензор деформации полностью характеризует дефрмацию среды, искомая величина должна выражаться через компоненты тензора деформаций.
4.1 Выражение для относительной деформации в заданном направлении.
Рассмотрим элемент такой, что и введем направляющие косинусы, определяющие направления элемента :
(76)
Ясно, что
По определению (213) относительной
деформации
:
где --- величина элемента после деформации. Отсюда, с учетом малости деформации:
или:
С другой стороны, согласно (206):
Сопоставляя это с предыдущим выражением, находим, что
Вспоминая, что , окончательно имеем:
(77)
Выражение (170) определяет
искомую величину относительной деформации
отрезка в направлении
.
Заметим, что эта величина зависит,
согласно (170), только от
направления исходного
отрезка и не зависит от его длины. Это
обстоятельство является следствием
линейности описания
деформации, которая, в свою очередь,
обусловлена малостью
деформаций.
4.2 Иллюстрация тензорной природы
.
Тензорная природа была нами установлена в section 1 на основании теоремы деления. Выражение (170) позволяет наглядно представить себе этот результат.
Введем новую систему координат
так, что ее ось
направлена вдоль заданного направления
.
Тогда в этой системе координат компонента
выражается в соответствии со своим
геометрическим смыслом согласно (170):
По определению вектора:
Но, очевидно,
Поэтому:
Подставляя это выражение для , найдем, что:
Учитывая, что для декартовых систем координат:
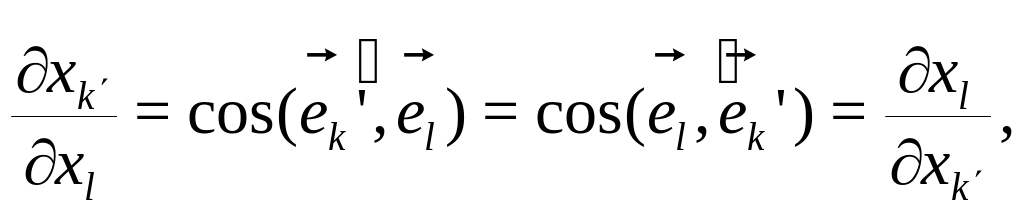
окончательно получим:
Это выражение соответствует определению тензора (??). Используя (170) можно получить аналогичные выражения для других компонент.
Т.о. выражение (170) наглядным
образом иллюстрирует тензорную природу
.
Заметим также, что (170) совпадает по
форме с выражением (??) введенным для
определения тензорной поверхности
(chapter 1. Поэтому условие
определяет тензорную поверхность для
тенгзора деформаций.
Резюме section 4.
Относительная деформация (удлинение или сжатие отрезка) в заданном направлении выражается через тензор деформаций.
1). Величина относительной деформации зависит от направления отрезка, но не зависит от его длины. Последнее обстоятельство является следствием линейности малой деформации.
2). Относительная деформация выражается двойной сверткой тензора деформации с направлением отрезка. В этом проявляется тензорная природа .
5 Главные оси, главные значения инварианты тензора деформаций.
Тензор деформаций, как и всякий симметричный тензор 2-го ранга может быть приведен к каноническому (диагональному виду (см. section 4, chapter 1.
5.1 Главные оси и главные значения.
В главных осях --- в системе
координат, оси которой совпадают с
главными направлениями тензора, ---
отличны от нуля только диагональные
элементы тензора деформаций, равные
его главным значениям.
Приведение тензора деформаций к такому
каноническому виду может быть осуществлено
в любой точке, в которой задан тензор
Поскольку диагональные элементы тензора деформаций --- суть относительные растяжения и сжатия, возможность приведения тензора деформаций к диагональному виду означает, что любую произвольную деформацию в данной точке можно представить как суперпозицию исключительно растяжений и сжатий в трех взаимно-перпендикулярных направлениях. Причем относительные величины эь]тих расстяжений и сжатий являются главными значениями тензора деформаций, а соответствующие ортогональные направления --- главными направлениями. Главные значения тензора деформаций называют также главными деформациями.
Напрмним основные уравнения для определения главных значений и главных напряжений тензора деформаций.
В каждой точке среды главные значения находятся как решения векового уравнения:
(78)
Будем их обозначать как
,
,
.
В каждой точке среды
главные направления
определяются из системы уравнений:
(79)
(80)
Будем обозначать их как .
напомним также, что если два главных значения совпадают, то картина деформации (в этой точке) симметрична относительно оси, совпадающей с главным направлением, отвечающим третьему главному значению. Примером такой деформации служит рассмотренное в section 3 одноосное растяжениею
Если все три главных значения тензора совпадают, то (в этой точке) деформация по всем направлениям одинакова. Заметим также, что в этом случае сдвиговые недиагональные элементы тензора деформаций равны нулю в любой системе координат, и, следовательно, такая ситуация отвечает всестороннему расширению (или сжатию).
Относительная деформация в произвольном направлении в главных осях имеет вид (согласно (170)):
(81)