1.4 Симметричность тензора напряжений.

Рассмотрим момент внутренних сил, действующих на элемент напряженной среды.

По определению, момент, отнесенный к единице объема, равен:

где --- объемная плотность сил.

Используя символ Леви-Чивиты, запишем следующим образом:

На элемент объема действует момент , а на весь выделенный объем:

Как и полная сила, действующая на объем ,момент сил должен выражаться через интеграл по поверхности элемента . Преобразуем , заменив на в соответствии с ((205) :

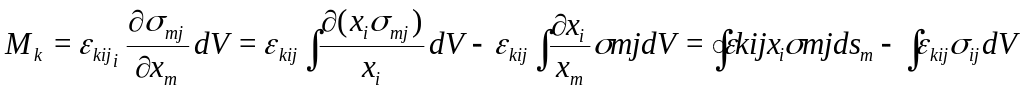
Момент будет выражен в виде интеграла только по поверхности, если второй интеграл равен 0. Отсюда, в силу произвольности элемента , находим, что:

Учитывая перестановочные свойства , приходим к заключению, что:

(105)

(207) выражает фундаментальное свойство тензора напряжений.

Заметим, что симметрия тензора напряжений является прямым следствием принципа Коши, или постулата сплошности среды.

Отметим также, что момент внутренних сил, действующих на некоторый объем среды, можно представить следующим образом:

(106)

Замечание. С учетом свойства симметрии тензора напряжений формулу Коши можно переписать:

(107)

Именно такая форма записи этого выражения традиционна в МСС.

Резюме ?1.

Рассмотрен вопрос о природе напряженного состояния сплошной среды и введена его основная характеристика --- тензор напряжений.

1. Силы, возникающие внутри деформированной среды являются поверхностными. Поэтому каждой площадке, выделенной мысленно внутри тела, может быть поставлен в соответствие вектор напряжений, эквивалентный действию на этиу площадку соседних частей среды.

2. Однозначное сопоставление вектора напряжений и нормали к площадке обеспечивает тензор напряжений, полностью характеризующий тем самым напряженное состояние среды.

3. Тензор напряжений --- симметричный тензор 2 --- го ранга. Его компоненты --- --- cуть ---я компонента вектора напряжений (усилия), действующего на --- й площадке.

2 Равновесие сплошной среды.

2.1 Уравнение равновесия.

Рассмотрим среду, на которую действуют внешние (объемные) силы с объемной плотностью . Выделим, как и в ?1, элемент среды объемом . На этот элемент действуют две силы: поверхностная и объемная . Элемент среды будет находится в равновесии, если сумма этих сил равна нулю:

Заменяя поверхностную силу выражением через , получим:

Откуда, в силу произвольности элемента среды , находим уравнение равновесия сплошной среды:

(108)

Или, с учетом симметрии :

(109)

В случае отсутствия внешних сил уравнение имеет вид:

(110)

Замечание. Часто вместо объемной плотности внешних, объемных сил используют их массовую плотность . Из соотношения:

Находим, что объемная и массовая плотности сил связаны соотношением:

Заметим, что величина имеет размерность ускорения.

Уравнение равновесия имеет в таком случае вид:

(111)