2.2 Октаэдрическая площадка.

При рассмотрении в рамках МСС вопросов, связанных в первую очередь с пластичностью и прочностью, существенную роль игоают площадки такие, что в главных осях т.е. 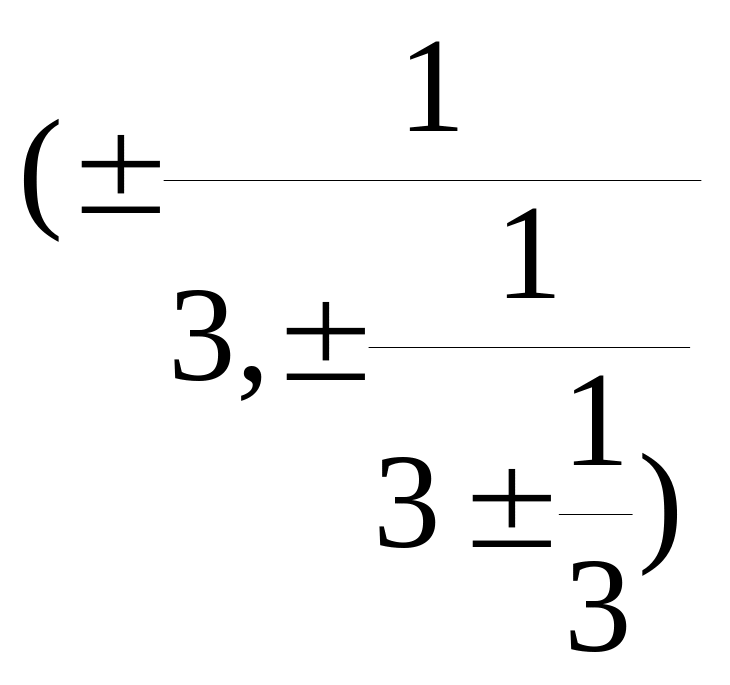. Такие площадки называют октаэдрическими (их всего 6, и они образуют поверхнсоть правильного октаэдра).

Согласно (222):

(127)

а

(128)

Касательные напряжения на октаэдрической площадке равны:

(129)

Или с учетом наблицы из предыдущего пункта:

(130)

Заметим, что выражения (226) и (129) можно переписать, используя (121), следующим образом:

и

Наконец, отметим, что

где --- второй инвариант девиатора напряжений.

Резюме

3 5

1. Площадки, на которых касательные напряжения в некоторой точке среды достигают своего максимального по абсолютной величине значения, проходят через одно из главных направлений и ориентированы под углом 45^ к двум другим главным направлениям. Величины максимальных касательных напряжений равны полуразности главных напряжений, отвечающих главным направлениям, ориентированным под углом 45^ к площадке.

2. На октаэдрической площадке нормальное напряжение равно среднему из главных напряжений, а квадрат полного усилия --- среднему из квадратов главных напряжений.

Заключение главы 3.

Напряженное состояние сплошной среды обусловлено действием на частицы среды внутренних сил (внутренних напряжений), возникающих в результате деформации среды, Внутренние силы, действующие со стороны одной части напряженной среды на другую ее часть, оказывают свое влияние только через поверхность, разделяющую эти части. Они эквивалентны приложению к этой поверхности определенных усилий. Поэтому внутренние силы называются поверхностными.

Напряженное состояние среды в каждой ее точке полностью описывается тензором напряжений. Этот тензор позволяет рассчитать усилие действующее на любой площадке, если задана ориентация этой площадки. Тензор напряжений является симметричным тензором второго ранга. Его компоненты --- --- суть: ---я компонента усилия, действующая на площадке, ортогональной ---ой оси координат.

Равновесие сплошной среды определяется равенством нулю равнодействующей поверхностных и массовых сил, приложенной к каждой точке среды. На поверхности тела равновесие определяется балансом внешних усилий и внутренних напряжений.

Произвольное напряжение в каждой точке среды можно разложить на суперпозицию нормальных напряжений (называемых главными), действующих в данной точке по трем взаимно-ортогональным площадкам (главным площадкам). Такое разложение соответствует приведению тензора напряжений к каноническому виду (к главным осям). На главных площадках касательные напряжения равны нулю, а нормальные достигают своих максимальных значений.

Касательные напряжения достигают своих максимальных значений на площадках, ориентированных под углом 45_ к двум главным осям и проходящих через третью.

4 Упругость.

Введение. Механические свойства сплошной среды.

Рассмотренные в предыдцщих главах деформированное и напряженное состояние среды могут относиться к любой среде: твердой, жидкой, вязкой, пластичной и т.д. Аппарат описания деформаций и напряжений не требует конкретизации механических свойств рассматриваемой среды.

В механическом смысле различные физические тела отличаются реакцией на прикладываемые воздействия --- нагрузки. Характер и особенности этой реакции и представляют собой, по сути, механические свойства тел. Поэтому, для того, чтобы ввести в рассмотрение в рамках МСС то или иное тело (т.е. среду с теми или иными свойствами) нужно установить закон его реакции на определенное воздействие. В математическом отношении это означает, что нужно задать связь между напряжениями и деформациями в каждой точке среды.

Уравнения, определяющие такую связь, являются математическим выражением механических свойств среды и называются определяющими соотношениями. Параметры, входящие в определяющие соотношения, являются константами вещества, количественно характеризующими свойства среды, и называются модулями.

Задание определяющих соотношений позволяет решить основную практическую задачу МСС: определение пространственно-временного распределения смещений точек среды по заданным массовым силам, нагрузкам и смещениям на ее поверхности.

Те или иные математические уравнения лишь в определенной мере отражают свойства реальной среды, являются ее моделью. Поэтому всегда следует полностью отдавать себе отчет в том, какие допущения сделаны при построении модели среды и каковы границы ее применимости. Заметим, что уже сама МСС накладывает на модели реальных сред весьма существенное ограничение --- а именно требование сплошности среды. Из общей теории МСС известны и другие требования, налагаемые на модели реальных сред. В частности, определяющие соотношения должны быть инвариантны относительно выбора системы координат и не противоречить законам термодинамики.

Модель среды можно строить на основе либо эмпирических обобщений, либо априорных требований и предложений, либо теории более общей, чем МСС.

Одна из простейших моделей среды --- линейная упругая модель,--- несмотря на свою простоту (а, возможно, благодаря ей) вполне удовлетворительно описывает широкий круг явлений реального мира, представляющих интерес для Земли. Соотношения, определяющие основные свойства этой модели --- упругость --- могут быть введены всеми тремя перечисленными способами. Мы рассмотрим первые два: обобщение эмпирических данных и априорное требование, определяющее понятие "упругость".