1 Символ Кронекера и тензор Леви-Чивиты.

Рассмотрим два тензора специального вида, имеющих широкое применение в механике сплошной среды.

1.1 Символ кронекера.

По определению символ Кронекера:

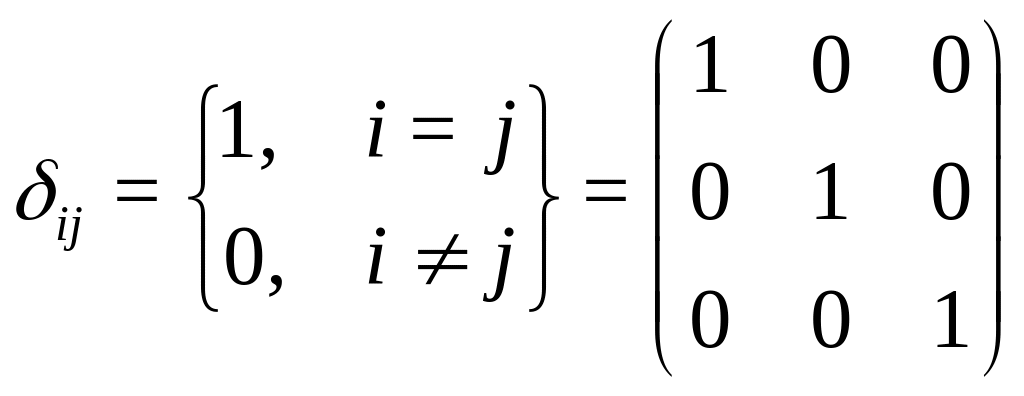
а). Свертка с вектором:

т.е.

(13)

Согласно теореме деления, выражение (213) свидетельствует о том, что --- тензор второго ранга.

б). Свертка с двумя векторами:

(14)

Из (191) следует, что

1.2 Тензор Леви-Чивиты.

По определению:

(15)

Определение (194) эквивалентно следующему определению:

и меняет знак при перестановке любой пары индексов.

Если число перестановок в последовательности 1 2 3 --- четно, то соответствующее значение , если нечетно, то . Если два индекса совпадают, то соответствующие компоненты тензора Леви-Чивиты равны нулю.

а). Свертка с двумя векторами.

(16)

--- векторное произведение:

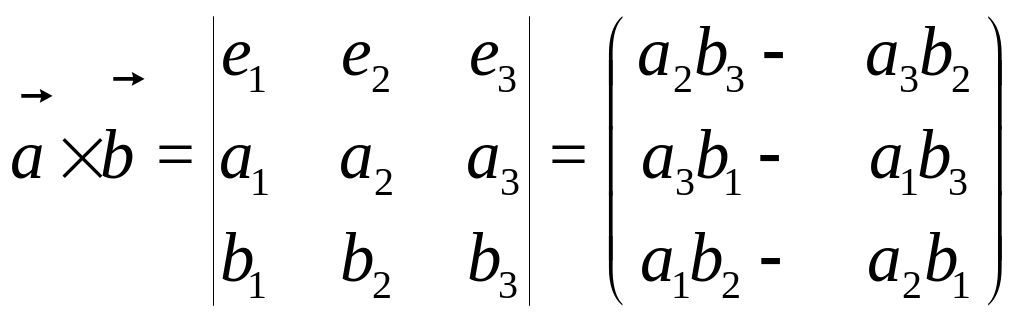
Из (138) при будем иметь:

Аналогично для и . Из (138) следует, что

Замечание. Выражение (138) свидетельствует о том, что --- тензор 3 - го ранга. Действительно:

--- тензор 2-го ранга, а b]_i --- вектор. Следовательно, согласно теореме деления, --- 3 -го ранга. б). Перестановочные свойства тензора Леви-Чивиты.

или:

в).Произведения и свертки тензора Леви-Чивиты.

Можно проверить, что

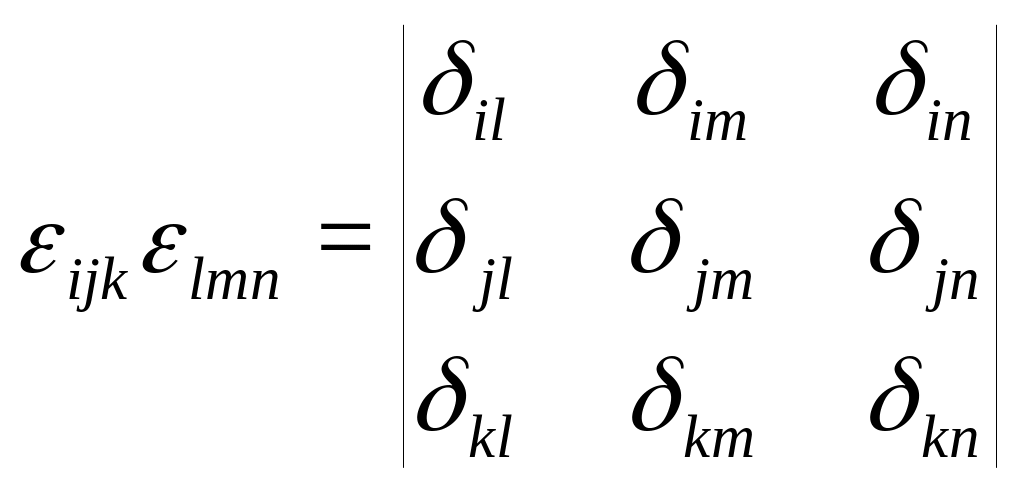(17)

(18)

(19)

(20)

Резюме section 2.

Введены два тензора специального вида и рассмотрены их свойства. 1.Символ Кронекера --- единичный тензор 2-го ранга. Может рассматриваться как оператор скалярного произведения векторов. 2. Тензор Леви-Чивиты --- единичный тензор 3-го ранга антисимметричный по всем индексам. Может рассматриваться как оператор векторного произведения векторов.

2 Дифференцирование и интегрирование тензоров.

Тензорные величины могут зависеть от координат, т.е. их компоненты могут быть функциями , , и , а также и времени. Поэтому следует рассмотреть вопрос дифференцирования и интегрирования тензоров.

Применение к тензорам операций дифференцирования или интегрирования сводится к применению этих операций к компонентам тензоров.

2.1 Дифференциальные операции.

а). Скалярная функция

С учетом соглашения о суммировании:

Введем еще одну форму записи: будем обозначать дифференцирование по через запятую:

Тогда:

(21)

Рассмотрим теиерь векторные дифференциальные операторы:

б).

или:

(22)

заметим, что оператор: в).

г).

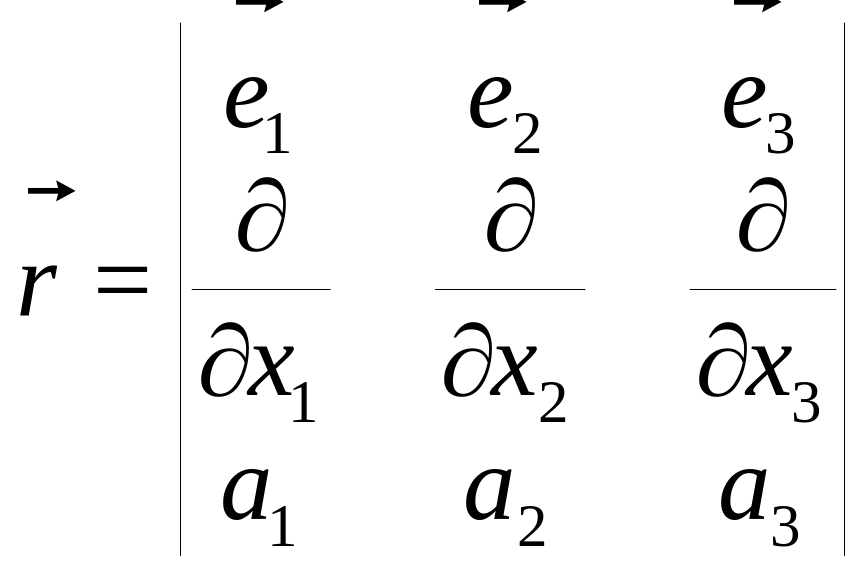
или, с учетом (138):

(23)

д).

или

(24)

Выражение (216) --- (199) можно использовать для обобщения векторных дифференциальных операций н аслучай тензоров ранга выше 1-го:

(25)

(26)

(27)

(28)

(29)

и т.д. е). Дифференцирование скалярного и векторного произведений.

т.е.

(30)

(31)

и так: