5.2 Поток энергии. Вектор Умова.

Определим поток энергии за счет упругих волн. По определению поток равен энергии, проходящей через единичную площадку за единицу времени.

Рассмотрим элемент среды в форме бруска с основанием и длиной , где и --- положения фронта волны, разделенные интервалом времени . ---направление нормали к фронту волны. Энергия, сосредоточенная в объеме выбранного элемента, равна

Следовательно, поток энергии в направлении через поверхность в точке равен, по определению:

где плотность энергии W определяется согласно (222).

Потоку энергии можно придать векторное толкование, обозначив

В случае упругих волн поток энергии равен таким образом:

(224)

Вектор потока P называется вектором Умова (в честь профессора Н.А.Умова). Он направлен по нормали к фронту волны. В однородной изотропной среде это направление совпадает с направлением распространения волны.

В случае гармонической волны средний (за период ) поток энергии равен:

(225)

Если в некоторой точке среды имеется источник упругих волн, то изменение его энергии равно суммарному потоку энергии через замкнутую поверхность, окружающую этот источник:

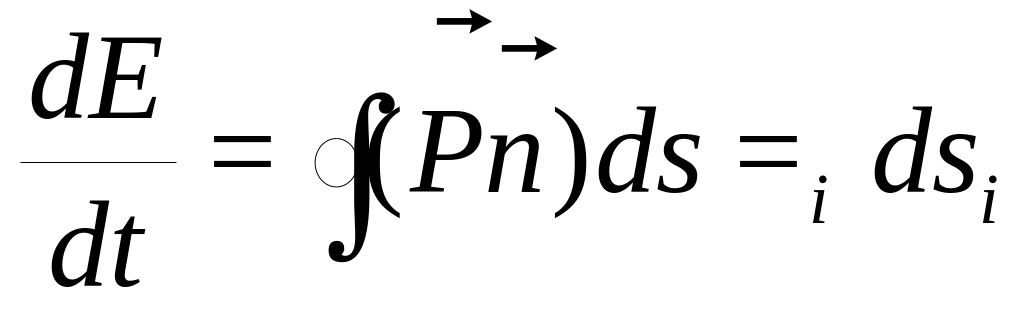(226)

Величина может быть определена экспериментально из наблюдений смещений на выбранной поверхности, окружающей источник (на основании выражения (224) или (225)). Поэтому, выражение (226) можно использовать для определения мощности источника волн , а в случае ограниченного во времени действия источника --- его суммарной энергии (интегрируя (226) по времени).

Этот метод заложен, в частности, в основу определения энергии землетрясений, взрывов и других источников упругих волн в Земле (сейсмических источников).

Резюме section 5.

1. В плоской упругой волне кинетическая энергия движения частиц равна потенциальной энергии дейормации среды . Это обстоятельство является следствием того, что в процессе упругих колебаний потенциальная энергия полностью переходит в кинетическую и обратно.

2. Плотность и поток энергии в упругих волнах пропорциональны квадрату скорости смещения частиц среды в волне, а в монохроматических волнах --- квадрату отношения амплитуды колебаний смещения к периоду.

6 Отражение и преломление упругих волн.

Рассмотрим падение объемных волн на границу раздела между двумя упругими средами с различными свойствами.

Свойства сред характеризуются их модулями и плотностью или скоростью распространения волн. Угол между направлением распространения волны и нормалью к поверхности будем называть углом падения (отражения, преломления) волн.

6.1 Граничные условия.

Для смещений в падающей, отраженной и преломленной волнах в средах 1 и 2 справедливы соответствующие волновые уравнения. При наличии границы решения этих уравнений --- движения в падающей, отраженной и преломленной волнах --- не являются независимыми. Они связаны условиями на границе раздела сред (при в нашем случае).