5.2 Инварианты тензора деформаций.

Определенные комбинации компонент тензора второго ранга инвариантны к операциям преобразования системы координат. В нашем случае инварианты тензора деформаций имеют вид:

(82)

(83)

(84)

Первый инвариант тензора деформаций имеет простой геометрический смысл. Для его выяснения найдем относительное изменение элемента объема при деформации.

Пусть до деформации элемент объема в главных осях имеет вид:

а для справедливо выражение:

(без суммирования по .

Учитывая малость деформации находим для :

Это можно переписать как

Сравнивая это с (225) обнаруживаем, что первый инвариант тензора деформаций равен относительному изменению объема при деформации. Эту величину называют дилатацией и обозначают обычно :

(85)

Т.о. сумма диагональных элементов тензора деформаций (в произвольной системе координат) --- суть относительное изменение объема при деформации. Вспминая, что , найдем, что

Второй и третий инварианты тензора деформаций не имеют столь простого геометрического смысла. Учитывая малость деформации, можно отметить, что

5.3 Шаровой тензор и девиатор деформаций.

Различные среды (упругие, жидкие, вязкие и др.) более или менее однотипно реагируют на всестороннее сжатие (растяжение) и по-разному --- на несимметричные деформации, содержащие сдвиговые компоненты. Поэтому, во многих приложениях МСС оказывается удобным представить тензор деформаций в виде суммы:

(86)

где

Тензор называется шаровым тензором (его тензорная поверхность является поверхностью шара). Он описывает осредненное по всем направлениям растяжение (сжатие) при деформации. Очевидно, что:

Тензор называется девиатором деформации и характеризует отклонение деформации от всестороннего расширения и сжатия.

Шаровой тензор описывает изменение объема, а девиатор --- изменение формы при деформации.

5.4 Дополнение. Иллюстрация: приведение тензора к каноническому виду.

Рассмотрим чистый сдвиг:

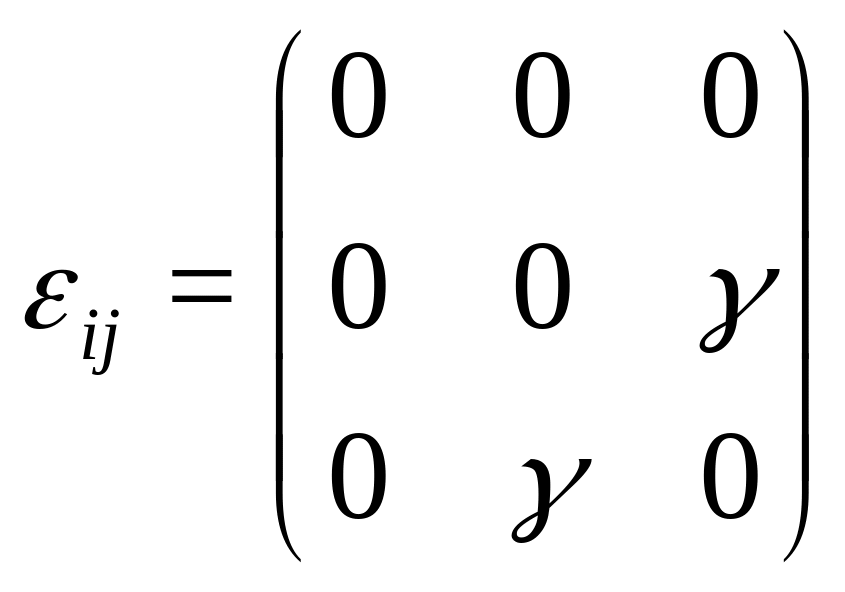
1. Главные значения . Из (222) имеем:

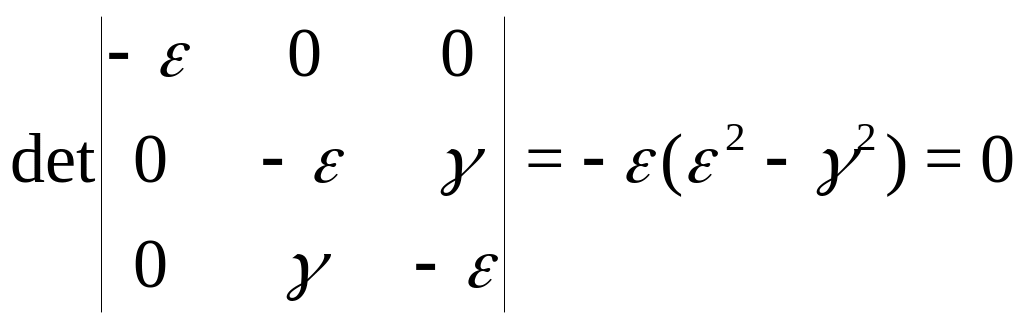
Следовательно: , , .

2.Главные направления.

Из (223)

(87)

(88)

(89)

Следовательно, в главных осях

т.е. сдвиг можно представить как суперпозицию растяжения и сжатия по двум взаимно перпендикулярным направлениям.

3. Инварианты.

(90)

(91)

(92)

Чистый сдвиг не изменяет объема.

. Шаровой тензор:

(93)

(94)

При сдвиге происходит только изменение формы. Замечание. Полученный результат легко проверить, используя выражение (170). Действительно, в направлении :

Аналогично, в направлении :

Резюме ыусешщт 5. 1. Операция приведения тензора деформаций в некоторой точке среды к каноническому, диагональному виду эквивалентна представлению деформации в этой точке в виде суперпозиции растяжений и сжатий по трем взаимно ортогональным направлениям. Величины относительных растяжений и сжатий являются главными значениями, а соответствующие направления --- главными направлениями тензора деформаций в этой точке. 2. Первый инвариант тензора деформаций имеет определенный геометрический смысл. Этот инвариант --- сумма диагональных компонент тензора --- равен относительному изменению объема при деформации. Эта величина называется дилатацией. 3. Всякая деформация может быть представлена как суперпозиция изменения объема и изменения формы элемента среды. Первая часть описывается шаровым тензором, вторая --- девиатором деформаций.