3.2 Нормальные напряжения.
Согласно (215):
Используя формулу Коши, найдем, что
(116)
Величина нормального напряжения на площадке заданного направления является билинейной формой компонент нормали . Заметим, что выражение (216) аналогично (??), выражающему деформацию отрезка в заданном направлении. Рассуждая также, как в
3.3 2
4 4
4 2
, можно использовать (216) для наглядной иллюстрации тензора природы , направляя ось новой системы координат вдоль и рассматривая (216) как закон преобразования от старой системы координат к новой, легко обнаружить, что отвечает определению тензора (??).
Отметим, что условие
определяет тензорную поверхность
тензора напряжений.
0.1 Касательные напряжения.
Из (215) следует, что
Выражая
через
--- согласно формуле Коши, легко найти
для :
(117)
Резюме
1 3
1. Вектор напряжений на каждой площадке можно разложить на нормальную и тангенциальную составляющие, называемые нормальными и касательными напряжениями на этой площадке.
2. Нормальное напряжение представляет собой билинейную форму от компонент вектора нормали площадки. Коэффициентами этой формы являются компоненты тензора напряжений.
2 Главные направления, главные значения, инварианты тензора напряжений.
Тензор напряжений, являясь симметричным тензором 2---го ранга, может быть приведен к каноническому виду. Рассмотрим вопросы, связанные с этой процедурой.
2.1 Приведение тензора напряжений к каноническому виду.
Пусть в некоторой точке среды
задан тензор напряжений
.
Найдем такие площадки
,
на которых в этой точке вектор напряжений
имеет только нормальную
составляющую (т.е. на которых
).
Согласно (215) на таких площадках:
что с учетом формулы Коши дает
или
(118)
Выражение (152) определяет
систему уравнений для нахождения главных
напряжений
и соответствующих главных значений
(см.
3 4
5 1
. Площадки, задаваемые векторами
называются главными
площадками. Главные
значения тензора напряжений являются
решениями векового уравнения:
(119)
Как известно, (170) имеет три
вещественных решения
.
Обычно
нумеруют таким образом, что:
Главные значения тензора напряжений называют также главными напряжениями.
Главные направления определяют площадки, на которых касательные напряжения равны нулю, а нормальные --- главным значениям .
В главных осях, совпадающих
с
,
тензор напряжений имеет вид:
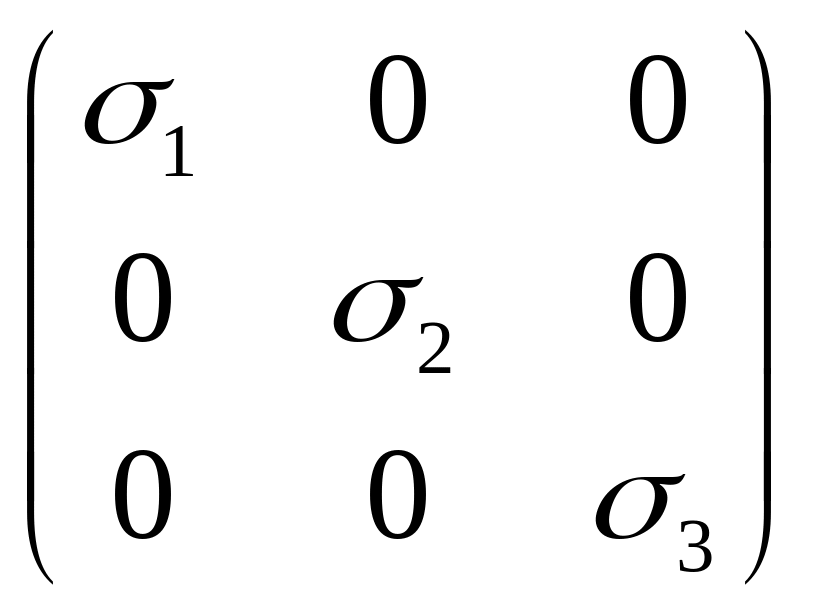
Согласно формуле Коши в главных осях вектор напряжений на площадке с произвольным направлением имеет компоненты:
(120)
Это означает, что процедура приведения тензора напряжений к каноническому виду в физическом отношении эквивалентна представлению усилия в данной точке среды по произвольной площадке (вектора ) как суперпозиции нормальных усилий в этой точке по трем взаимноортогональным направлениям.
Инварианты тензора имеют вид:
(121)
Если в некоторой системе координат известны главные направления и главные значения тензора напряжений, то в ней можно легко найти компоненты тензора напряжений (см. выражение (??)):
(122)