3.3 Закон сохранения энергии при движении сплошной среды.

Выберем в качестве начального состояния среды в момент времени ее недеформированное состояние покоя. Т.е. будем считать, что и

где --- смещения точек среды за интервал . Очевидно, что: _i . Выражая из уравнения движения (202), получим:

_i Последние два интеграла в случае однородной упругой среды равны , где --- упругая потенциальная энергия деформации (??).

Первый интеграл можно преобразовать следующим образом:

_i dotu_i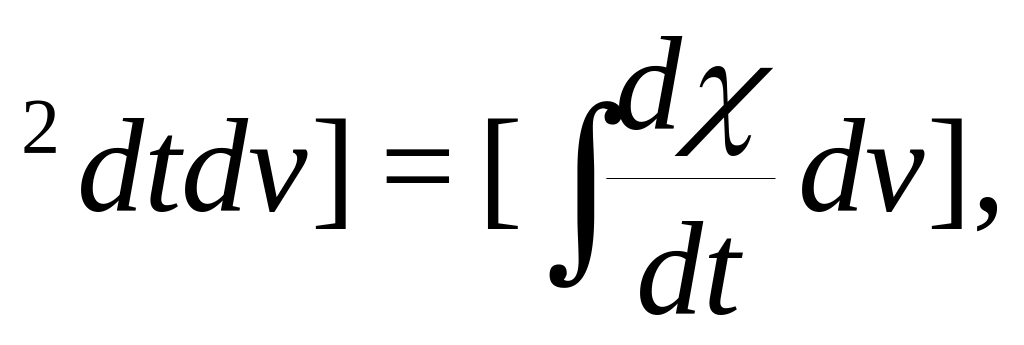 где через обозначена кинетическая энергия единицы объема:

Учитывая, наконец, что , получаем:

или:

Интегрируя теперь это выражение от до , находим окончательно:

(194)

Выражение (194) означает, что работа внешних сил при деформировании однородной упругой среды расходуется на создание кинетической энергии движения среды и потенциальной энергии ее деформации.

Таким образом (194) выражает закон сохранения энергии при движении однородной упругой среды.

Резюме

4 2

1.Уравнение движения для упругой среды может быть сведено к уравнению непосредственно для смещений точек среды. В случае однородной изотропной упругой среды уравнение движения в такой форме называют уравнениями Ламе. 2. Работа массовых сил и усилий на поверхности тела при движении однородной упругой среды расходуется на создание кинетической энергии движения и потенциальной энергии деформации среды.

5 Теоремы единственности и взаимности.

В этом параграфе будут доказаны единственность решения уравнения движения однородной упругой среды и так называемая теорема Бетти, связывающая искомое решение уравнения движения с другим неизвестным решением этого уравнения. Теорема Бетти имеет принципиальное значение в теории источника волн в упругой среде, она позволяет обобщить метод функции источника на случай тензорного поля.

5.1 Начальные и граничные условия к уравнению движения.

Уравнения движения представляют собой систему дифференциальных уравнений 2-го порядка в частных производных. Поэтому в качестве начальных условий к эти уравнениям для всех точек (частиц) среды следует задать значения смещений и скоростей движения

в начальный момент времени:

(195)

Граничные условия могут быть заданы различным образом. 1. Заданием усилий на всей поверхности тела в каждый момент времени

(196)

2.Заданием смещений на всей поверхности тела в каждый момент времени :

(197)

3.Заданием на одной части поверхности усилий, а на остальной части --- смещений:

(198)

5.2 Теорема единственности.

Если существует решение уравнения движения однородной упругой среды (213) с начальными условиями (215) и граничными условиями (198), то это решение единственно.

Пусть существует два решения поставленной задачи: и . Покажем, что они совпадают, что и докажет единственность решения уравнения движения.

Рассмотрим разность . В силу линейности уравнения движения (213) также удовлетворяет уравнению движения (213), но уже с :

Начальные условия (216) для также однородны: и

В граничных условиях (198), очевидно, , Условия на границе для решения имеют вид:

где и ---напряжения, обусловленные смещениями и соответственно. Поскольку согласно (198)

в случае имеем:

Таким образом, смещения удовлетворяют однородному уравнению движения с нулевыми начальными и граничными условиями. Отсюда следует, что и .

Действительно, поскольку внешние силы и усилия равны нулю для любого , равна нулю и их работа в интервале времени от до любого . Согласно закону сохранения энергии (194) это означает, что

(199)

Поскольку и , условие (199) может быть выполнено только тогда, когда

Это означает, что

(200)

С учетом однородности начальных и граничных условий для из этих уравнений следует, что

Тем самым теорема единственности доказана.