2.2 Уравнение моментов.

Пусть среда находится в равновесии. Покажем, сто в этом случае суммарный момент поверхностных и объемных сил равен нулю.

Момент объемных сил имеет вид:

а момент поверхностных сил, согласно (209):

Поскольку среда находится в равновесии, из уравнения (213) имеем:

Следовательно:

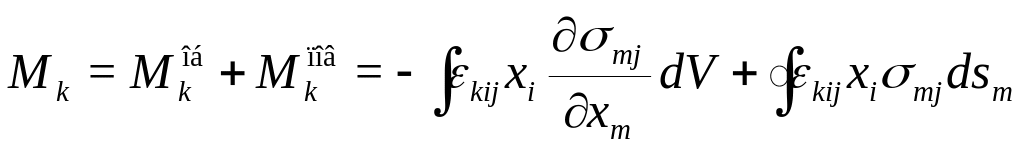
Преобразуя первый интеграл также, как и в п.4*?1 и учитывая симметричность , придем к тождеству:

(112)

В случае отсутствия объемных сил, условие (194) означает, что внутренние напряжения распределяются таким образом, что не создают момента. Это обстоятельство является очевидным следствием симметричности тензора напряжений.

Действительно, рассмотрим напряженный элемент кубической формы. Очевидно, что момент поверхностных сил, например, относительно оси 1, равен нулю, если

2.3 Условие равновесия на поверхности тела.

Уравнение равновесия сплошной среды, полученные в п.1*, следует дополнить граничными условиями.

К поверхности тела могут быть приложены внешние силы (которые обычно и вызывают деформацию тела). Пусть --- внешняя сила, действующая на единицу площади поверхности --- внешнее усилие. На элемент поверхности действует, таким образом, сила . В равновесии она должна компенсироваться действующей на этот же элемент силой, обусловленной внутренними напряжениями . Эта сила равна

Условие равновесия на внешней поверхнсоти имеет, следовательно, вид:

С учетом формулы Коши это условие принимает вид:

(113)

2.4 Средние значения тензора напряжений.

Зная распределение нагрузок по поверхности тела, можно рассчитать средние по объему величины компонент тензора напряжений. Получим соответствующее выражение в случае отсутствия объемных сил.

Умножим уравнение равновесия (191) на и проинтегрируем по объему тела:

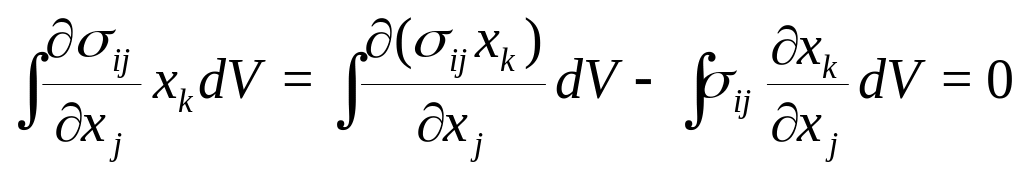
Или

Подставляя сюда условие (138), находим:

Учитывая симметричность тензора напряжений, это выражение можно переписать в симметричном виде:

(114)

Выражение (114) позволяет определитьт среднее по объему значение тензора напряжений, не решая уравнения равновесия (191).

Резюме ?2.

Рассмотрено равновесие сплошной среды.

1. Равновесие сплошной среды обеспечено балансом внешних объемных (массовых) и внутренни поверхностных сил.

2. В равновесном состоянии суммарный момент объемных и поверхностных сил равен нулю. В отсутствии внешних объемных сил равенство нулю момента поверхностных сил обусловлено симметричностью тензора напряжений.

3. На поверхности среды внешние, приложенные к ней, усилия компенсируются внутренними усилиями, обусловленными напряженным состоянием среды.

4. Знание распределения внешних усилий по поверхности тела позволяет рассчитать средние по объему тела значения компонент тензора напряжений.

3 Нормальные и касательные напряжения.

3.1 Разложение вектора напряжений.

Вектор напряжений , действующий на площадке , можно представить в виде суммы 2---х векторов. Один из них направим вдоль нормали к площадке , а второй --- в плоскости этой площадки, вдоль .

Первый вектор называется нормальной, а второй --- тангенциальной составляющеми вектора вектора напряжений, или нормальным и касательным напряжениями.

Очевидно, что

(115)

и , .

Поскольку тензор напряжений полностью характеризует напряженное состояние среды, величины и можно выразить через , если задана .