3.3 Приведение тензора к каноническому виду.

Выберем в качестве базиса системы координат три взаимно-ортогональных главных направления тензора . Оси такой системы координат называют главными осями. Покажем, что в такой системе координат, или, как говорят, в главных осях, рассматриваемый тензор имеет только диагональные компоненты, которые равны его соответствующим главным значениям. Такая форма тензора называется канонической.

Обозначим тензор , записанный в главных осях, как , а базисные векторы главных осей --- как , так, что:

(46)

(47)

(48)

Для справедливо, по условию, выражение (171):

Положим в этом выражении :

clc r'=1 a_11 -a_1 =0

i=2 a_21 =0

i=3 a_31 =0 Отсюда находим, что и, с учетом симметричности :

При : clc i=2 a_22-a_2 =0

i=3 a_32 =0 Следовательно: и . Наконец, при : , т.е. Итак мы обгаруживаем в главных осях:

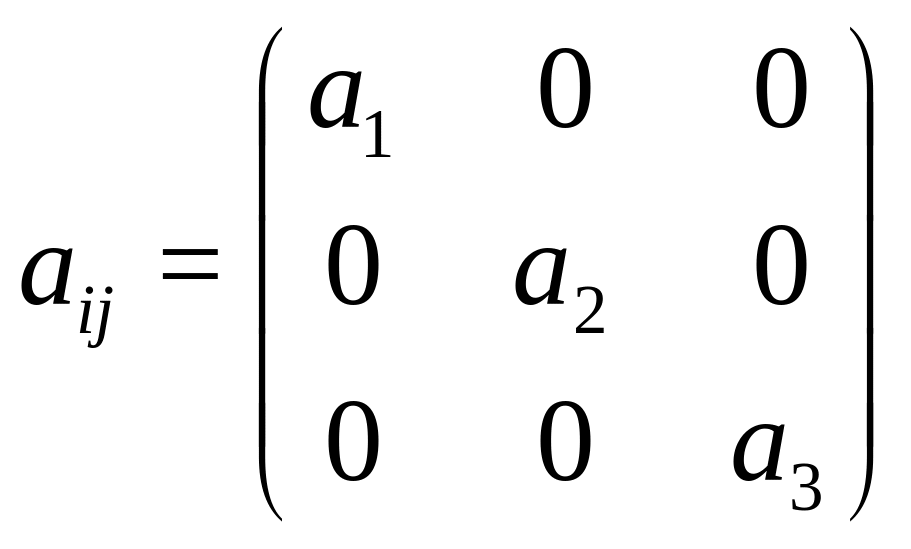(49)

Таким образом, симметричный тензор в главных осях имеет каноническую форму (49). Справедливо и обратное утверждение: если тензор в некотором базисе имеет канонический вид (49), то векторы этого базиса определяют главные направления рассматриваемого тензора, а диагональные элементы являются его соответствующими главными значениями. (Это утверждение легко доказать, свернув такой тензор с базисными векторами). 1). Используя выражения (123) и (49) можно выразить инварианты тензора через его главные значения:

(50)

(51)

(52)

2). Зная главные значения тензора и направления его главных осей , заданные в некоторой системе координат, можно выразить компоненты тензора в этой системе координат. Для этого достаточно воспользоваться формулой перехода от тензора в одной системе координат --- в главных осях --- к другой рассматриваемой (выражение (209)). Проделав это, найдем, что:

(53)

3.4 Тензорная поверхность.

Рассмотрим скалярное произведение векторов и :

Введем обозначение:

и наложим условие:

(54)

Это условие определяет в пространстве некоторую поверхность второго порядка, называемую тензорной поверхнстью.

Рассмотрим некоторые ее свойства . 1). Из определения следует, что 2).Приведение тензора к канонической форме соответствует приведению тензорной поверхности к каноническому виду. Согласно (54) в главных осях:

Отсюда видно, что квадраты полуосей тензорной поверхности обратно пропорциональны главным значениям соответствующего тензора. 3). Совпадение 2-х главных значений тензора означает, что тензорная поверхность является поверхностью вращения (имеет ось симметрии). Если все три главных значения тензора совпадают, то тензорная поверхность является сферой.

Резюме section 4.

Рассмотрены основные свойства симметричного тензора 2-го ранга, имеющего широкое применение в МСС.

1. Всякий симметричный тензор 2-го ранга эквивалентен линейному самосопряженному оператору в пространстве векторов. Действие такого оператора на некоторый вектор описывается сверткой тензора с этим вектором. 2. Для любого симметричного тензора 2-го ранга можно найти по крайней мере три взаимно-ортогональных вектора, свертка тензора с которыми сводится к умножению векторов на определенные скаляры. Эти скаляры называются главными значениями тензора, а направления в пространстве, определяемые указанными векторами, --- главными направлениями. Главные значения и главные направления являются решениями задачи на собственные значения линейного оператора в векторном пространстве.

3). В системе координат, оси которой совпадают с главными направлениями, тензор имеет канонический вид: его недиагональные компоненты равны нулю, а диагональные --- главным значениям.

4). Главные значения и главные направления тензора полностью его характеризуют --- зная их, можно рассчитать компоненты тензора в любой системе координат.

5). Геометрически всякий тензор 20го ранга характеризуется тензорной поверхностью

Заключение к главе 1.

В этой вводной главе приведена сводка основных понятий тензорного исчисления. Рассматривались только декартовы системы координат. 1. На основании обобщений понятий скаляра и вектора введено понятие тензора как математического объекта, инвариантного к преобразованию системы координат. 2.Применительно к тензорам рассмотрены флгебраические, дифференциальные и интегральные операции. Некоторые фундаментальные понятия, операции и теоремы векторного анализа обобщены на случай тензора произвольного ранга. 3. Подробно рассмотрены свойства тензоров 2-го ранга, играющих существенную роль в МСС. 4. Введены специальные тензоры-символы Кронекера и тензор Леви-Чивиты, позволяющие в компактной форме записывать выражения, включающие тензорные величины.