5.3 Теорема Бетти(e.Betti).

Пусть --- решение уравнения движения однородной упругой среды с массовыми силами и усилиями на ее границе , а --- решение того же уравнения движения, но с другими массовыми силами и усилиями . начальные условия для и --- поизвольные, но считаются заданными.

Тогда справедливо соотношение:

(201)

Доказательство.

Преобразуем левую часть (201), подставив в нее уравнение движения (202) и условие равновесия на поверхности (??)

Аналогичным образом, для правой части (201) найдем:

Сопоставляя выражения для левой и правой частей и учитывая симметричность тензора модулей упругости: , приходим к заключению, что (201) является тождеством. Тем самым теорема Бетти доказана.

Теорема взаимности Бетти связывает между собой решения уравнения движения однородной упругой среды, полученные при различных внешних силах. тем самым она открывает возможность использовать известные решения при достаточно простых условиях для отыскания решения при заданных, обычно более сложных силах. Так, в частности, при силах, заданных в виде --- функции, легко получить решение уравнения движения, называемое функцией Грина. Теорема Бетти позволяет представить решение уравнения движения при произвольных условиях в виде свертки этих условий и функции Грина. Такой метод лежит, в частности, в основе описания источника упругих волн (землетрясения в приложении к сейсмологии).

Замечание.

В выражении (201) можно перегруппировать члены следующим образом:

Что, после подстановки сюда уравнения движения (202), условий равновесия на границе (??) и закона Гука, дает:

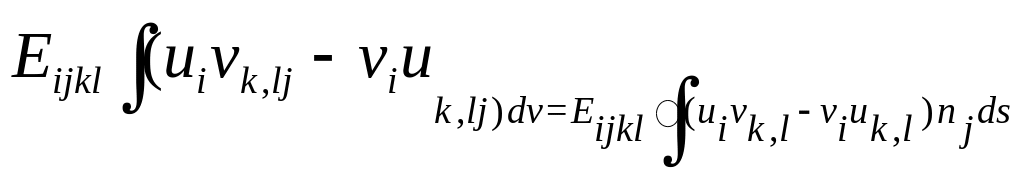
Это выражение является обобщением известной теоремы Грина для лапласиана на случай вторых производных от векторов. Напомним, что теорема Грина имеет вид:

или в тензорной форме записи:

Теорема Грина является инструментом для изучения неоднородных уравнений вида

Аналогично, теорема Бетти может быть использована для исследования неоднородных уравнений упругости, где неоднородность определяется массовыми силами .

Резюме

6 Теорема единственности и взаимности.

1.Уравнение движения однородной упругой сплошной среды при заданных начальных и граничных условиях имеет единственное решение. Начальные условия определяются заданием смещений частиц и их скоростей в начальный момент времени. Граничные условия определяются заданием усилий или смещений на границе тела.

2.Два решения уравнения движения однородной упругой среды, полученные при различных массовых силах и граничных условиях, связанны интегральным соотношением (теорема Бетти). Это соотношение открывает возможность представления решения при заданных условиях в виде суперпозиции "элементарных" решений, полученных при достаточно простых условиях.

Заключение chapter Уравнение движения упругой среды.

В случае произвольной среды уравнение движения включает в себя как динамические (напряжения), так и кинематические (смещения) характеристики состояния сплошной среды. Для того, чтобы найти смещения точек среды (обычно и представляющие практический интерес) необходимо дополнить уравнение движения сплошной среды определяющими соотношениями, т.е. ввести в рассмотрение модель среды.

Для однородных упругих сред уравнение ьдвижения сводится к дифференциальным уравнениям второго порядка в частных производных относительно смещения. В случае однородной и изотропной среды эти уравнения называются уравнениями Ламе.

Уравнения движения однородной упругой среды при заданных начальных и граничных условиях имеют единственное решение. Решения уравнения движения при различных внешних силах связаны интегральным соотношением (теорема взаимности Бетти).

Работа внешних сил при движении сплошной среды расходуется на создание кинетической энергии движения точек (частиц) среды и потенциальной энергии деформации среды.