Метод множителей Лагранжа.

Метод множителей Лагранжа в отличие от предыдущего подхода, позволяет решать задачи оптимизации того же порядка сложности, но с ограничения на переменные типа равенств. Суть метода заключается во введении p неопределенных множителей и построении функции Лагранжа

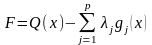
Для определения оптимальных значений переменных 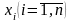решают систему из n+p уравнений

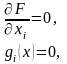
(9)

относительно неизвестных x и λ.

Если (9) представляет собой систему нелинейных уравнений, то трудности их решения аналогичны решению системы (4). Следует отметить, что система (9) – это лишь необходимые условия существования экстремума; поэтому найденные решения необходимо проверить на экстремум анализом производных более высокого порядка или другими методами.

Для примера рассмотрим следующую задачу. По плану производства предприятию необходимо изготовить 180 изделий (например, сборки агрегатов ЛА). Эти изделия могут быть изготовлены двумя технологическими способами. При производстве х₁ изделий

I способом затраты равны

4х₁+х₁² (руб.)

А при изготовлении х₂ изделий II способом они составят 8х₂+х₂² (руб.)

Определить, сколько изделий каждым из способов следует изготовить, так чтобы общие затраты на производство продукции были минимальными.

Математическая постановка состоит в определении минимального значения функции

f =4x₁+x₁²+8x₂+x₂²

при условиях

x₁+x₂=180, (10)

x₁,x₂≥0

Составим функцию Лагранжа

F(x₁,x₂,λ) = 4x₁+x₁²+8x₂+x₂²+λ(180-x₁-x₂),

Вычислим ее частные производные по х1, х2, λ и приравняем их нулю:

(11)

Перенося в правые части первых двух уравнений λ и приравнивая их левые части, получим

4+2х₁=8+2х₂, или х₁-х₂=2 (12)

Решая последнее уравнение (12) совместно с уравнением (10) находим

х₁*=91 и х₂*=89

Используя вторые частные производные, можно показать, что в найденной точке функция f имеет условный минимум.

Динамическое программирование.

Метод динамического программирования является одним из эффективных методов оптимизации многостадийных процессов и многоступенчатых систем.

Под стадией процесса понимают единичный элемент его разбиения во времени или пространстве, характеризуемый определенной совокупностью определяющих состояние процесса параметров. Например, в качестве стадий технологического процесса изготовления детали можно рассматривать технологические операции.

Под ступенью системы понимают единичный элемент его разбиения на составные части, каждая из которых характеризуется определенной совокупностью параметров. В качестве ступеней такой системы как летательный аппарат логично рассматривать, например, агрегаты, отдельные узлы и детали.

Критерии оптимальности многостадийных и многоступенчатых систем обычно представляют в виде аддитивной или мультипликативной функций критериев для отдельных стадий и ступеней. В первом случае значение общего критерия оптимальности равно сумме значений критериев отдельных стадий и ступеней, во втором случае – их произведению. Аддитивными являются, например, критерии, определяющие стоимость процесса, трудоемкость изготовления и др. Мультипликативным критерием может быть общая вероятность изготовления изделия соответствующего качества, равная произведению вероятностей выпуска годных изделий на каждом этапе технологического процесса.

Метод динамического программирования основан на принципе оптимальности Беллмана, который формулируется следующим образом: оптимальная стратегия обладает таким свойством, что каковы бы ни были начальное состояние и начальные решения, последующие решения следует принимать, исходя из оптимальной стратегии с учетом состояния, вытекающего из первого решения.

Математическую формулировку принципа оптимальности для дискретных процессов можно выразить в виде уравнения

(13)

где f_N(x₁) – максимальное значение критерия оптимальности для N стадий процесса; Х₁ и Х₂ – вектора параметров состояния соответственно на первой и второй стадии; U₁ – вектор управления на первой стадии; U – допустимое множество управлений; Q₁(X₁,U₁) – значение критерия оптимальности для первой стадии; f_N-1(X₂) – максимальное значение критерия оптимальности для N-1 стадий процесса от последней стадии.

Уравнение (13) представляет собой рекуррентное соотношение, определяющее связь между N-й и (N-1)-ой стадиями процесса, считая от последней. Оно позволяет, зная оптимальные управления для N-1 стадии процесса, считая от последней стадии, и зависимость f_N-1(x₂), определить оптимальное управление U_1opt.

Сущность метода динамического программирования заключается в том, что решение исходной задачи N-стадийного процесса сводится к решению последовательности задач: двухстадийной, трехстадийной и т.д. вплоть до N-стадийной. При этом определение оптимальных уравнений начинают с последней стадии. Задачи указанной последовательности решают с использованием рекуррентного соотношения (13).

Следует отметить, что существует множество задач, которые можно решить методом динамического программирования; причем, используя этот метод, можно довольно просто решить ряд задач, решение которых другими методами невозможно или чрезвычайно сложно.

По сравнению с комбинаторными методами динамическое программирование имеет значительные преимущества. Так для N-стадийного процесса с n возможных состояний на каждой стадии общее число переборов составляет n^N, а метод динамического программирования потребует просмотра N·n вариантов.

Рассмотрим использование метода динамического программирования для оптимизации структуры процессов изготовления элементов летательных аппаратов из трехслойных сотовых конструкций.

Выбор того или иного способа реализации технологического процесса изготовления элементов ЛА из композиционных материалов оказывает существенное влияние, как на частные технические решения, так и на принцип построения конструкции.

При этом конструкцию можно рассматривать как сложную систему &, принадлежащую множеству S, которое есть отношение на непустых множествах объектов производства R и технологических процессов Т:

где 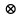- знак декартова произведения.

Задача оптимального выбора конструкции &* S решается в условиях разнообразия элементов множеств R и Т; R задается как отношение на множествах объектов производства r_j j-го наименования:

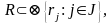
Где 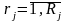- множество объектов производства j-го наименования; J – множество наименований объектов производства.

Технологический процесс наряду с внешними системными связями имеет сложную внутреннюю структуру. Он формируется путем объединения технологических операций в соответствии с некоторой технологической схемой, связанной с преобразованием объекта производства. Технологический процесс можно представить в виде отношения

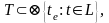
где 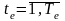- множество наименований технологических операций l-го наименования; L – множество наименований технологических операций.

Разнообразие множеств R и Т приводит к многоальтернативному заданию системы &. Технико-экономические показатели каждого варианта системы определяются желательными значениями некоторого набора показателей F_i (i=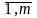 ). Поиск оптимального варианта приводит к необходимости организации эксперимента на ЭВМ с многоальтернативными оптимизационными моделями сложных систем, который позволяет осуществить выбор варианта системы с наилучшими показателями F_i* при объединении элементов из множества R в одно организационное целое & с помощью принадлежащей множеству Т формы воздействия. Оптимизационная модель в этом случае представляется как задача оптимального выбора с одной или несколькими целевыми функциями и ограничениями на множестве альтернатив.

Конструкция стабилизатора ЛА, изображенного на рис.3.15. состоит из следующих основных элементов: передний и задний лонжероны (1); нервюры (2); сотовые панели (3); носок стабилизатора (4); законцовка стабилизатора (5).

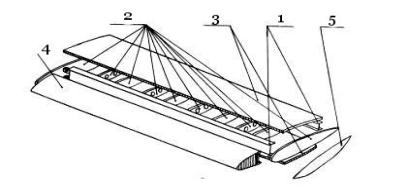
Рис. 3.15.

Технологические схемы процессов изготовления трехслойной клееной панели имеют достаточно много вариантов и сложную структуру. Эти варианты могут быть представлены в виде графа, узлы которого обозначают отдельные этапы процесса, а дуги определяют возможные их сочетания и порядок следования. Каждой дуге графа могут быть поставлены в соответствие тела, которые характеризуют изменение различных свойств в процессе изготовления. В качестве таких характеристик можно использовать технологическую себестоимость, изменение массы конструкции, время изготовления и т.п.

На рис.3.16 представлен граф возможных этапов процесса изготовления трехслойной панели 3 (рис.3.15). На рисунке приняты следующие обозначения: S₁ – материал сотового заполнителя; t₁ – хлопчатобумажная ткань; t₂ – стеклоткань; t₃ – толстая стеклоткань; t₄ – бумага; t₅ – фольга алюминиевая; S₂ – изготовление сотового заполнителя; t₆ – профилирование листов ткани, пропитанных связующим, с последующим склеиванием из них блоков; t₇ – профилирование листов, склеивание из них блоков с последующей пропиткой связующим; t₈ – изготовление сотового заполнителя из фольги, S₃ – подгонка размеров; t₉ – подгонка размеров элементов конструкций; S₄ – подготовка поверхностей к склеиванию; t₁₀ – обезжиривание под фенольнокаучуковые клеи; t₁₁ – обезжиривание под клей на эпоксидной основе; S₅ – выбор состояния массы клея; t₁₂ – клей жидкий; t₁₃ – клей плёночный; t₁₄ – клей твёрдый (порошок, расплав); S₆ – определение способов нанесения клея; t₁₅ – нанесение клея кистью; t₁₆ – нанесение клея пульверизатором; t₁₇ – нанесение клея валиком; t₁₈ – нанесение клея прокаткой роликами; t₁₉ – нанесение клея-порошка на подогретую поверхность; t₂₀ – нанесение клея-расплава валиком на специальной установке; S₇ – установка обшивки; t₂₁ – склеивание элементов конструкции между собой; S₈ – склеивание слоистой конструкции; t₂₂ – склеивание в вакуумных мешках; t₂₃ – склеивание в автоклаве; S₉ – контроль геометрии и точности; t₂₄ – проверка геометрических параметров и точности изготовления; S₁₀ – контроль качества склеивания; t₂₅ – разрушающий метод контроля; t₂₆–неразрушающий контроль качества склеивания.

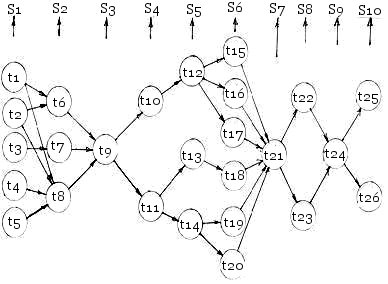
Рис. 3.16.

Для постановки и решения задачи определения оптимального процесса изготовления готовой конструкции введём следующие переменные:

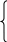1, если процесс t_j выполняется после t_i;

X_i,j= 0, в противном случае.

a_k, если t_j-й процесс изменяет массу конструкции;

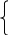G_ij= 0, в противном случае

Тогда оптимизационная модель запишется в виде:

при ограничениях

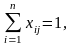
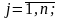
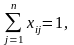
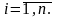
Для решения поставленной задачи можно использовать рекуррентное соотношение вида (13):

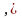
где f_n (t) – масса конструкции, отвечающая стратегии минимальной для последовательности от этапа процесса t, если до конечного этапа осталось n шагов; j_n (t) – решения, позволяющие достичь f_n (t).

Используя алгоритм решения поставленной задачи, получим последовательность операций, обеспечивающих минимальную массу изготавливаемой конструкции:

t₅ – t₈ – t₉ – t₁₁ – t₁₄ – t₂₀ – t₂₁ – t₂₃ – t₂₄ – t₂₆

Характерной особенностью сформированного технологического процесса является использование клея-расплава, который наносится на готовый блок валиком на специальной установке. Полученное решение согласуется с современной практикой изготовления готовых конструкций, что подтверждает адекватность используемой математической модели.

Подобную задачу относительно всего агрегата, а в этом случае исходный график будет иметь значительно больше узлов, можно решать с использованием ЭВМ.