Приложение 1. Дельта-функция Дирака

Общие свойства

По определению дельта-функцияδ(t-t₀) для любой действительной величины t₀ равна нулю при t≠t₀и неограниченно велика приt=t₀

(П1.0)

Интеграл от этой функции

(П1.0)

Дельта-функция – это предельная функция от однопараметрического семейства непрерывных функций, причем примеров таких семейств очень много. Рассмотрим, например, совокупность s(t,τ) прямоугольных импульсов единичной площади, длительность которых составляет τ, а высота 1/τ

(П1.0)

Если длительность импульса τ устремить к нулю, то в результате предельного перехода получим дельта-функцию.

Альтернативным вариантом получения δ-функции может быть

.

(П1.0)

Если дельта-функция δ(t-t₀) выступает в качестве сомно­жителя при любой ограниченной и непрерывной в точке t₀ функции f(t), то интеграл от подобного произведения определяется так называемым фильтрующим свойством дельта-функции

(П1.0)

Если же функция f(t) имеет в точкеt₀ разрыв (первого рода), то фильтрующее свойстводельта-функции приобретает вид[3]

,

(П1.0)

где изначенияf(t) слева и справа от точки разрыва.

Свойства производных дельта-функции

Производные от дельта-функции определяются как пределы соответствующих производных от аппроксимирующих функций. Например, используя (П1.0), для первой производной дельта-функции имеем

.

(П1.0)

Нетрудно видеть, что при любом t≠0 эта производная принимает нулевые значения, а в самой точкеt=0 наблюдается разрыв, причем производная стремится к +∞ при подходе к точке разрыва слева и к –∞ при стремлении кt=0 справа. На про­изводные распространяются и фильтрующие свойства дельта-функции. Свертка производной дельта-функцииn-го порядка с любой функцией, имеющей непрерывную в точкеt₀производнуюn-го порядка равна

,

(П1.0)

Любопытно, что существуют и иные функции, обладающие фильтрующим свойством, например, функция sin(x) / x. Если f(x)непрерывна в точкеx = a, то

.

(П1.0)

Спектральные характеристики дельта-функции

Из фильтрующего свойства дельта-функции следует

,

(П1.0)

т.е. спектр дельта-функции равномерный на всех частотах и имеет единичную интенсивность. Соответственно, спектр полусуммы двух дельта-функций 0,5 · [δ(t-t₀)+δ(t+t₀)] равен

.

(П1.0)

Для обратного преобразования Фурье получаем соответственно

,

(П1.0)

а также

.

(П1.0)

Размерность и особенности нормировки

Размерность дельта-функции обратна размерностиеё аргу­мента, т.е. если аргументом дельта-функции служит времяt, выражаемое в секундах, то значенияδ(t-t₀) выражаются в «1/c», а для функции δ(u-u₀), аргументом которой служит напряжение, результаты будут выражаться в «1/В».

Дельта-функции нередко появляются в составе плотности вероятности, спектральной плотности мощности и т.п., то есть характеризуют плотностьy(x)рас­пределения некоторой вели­чины Y вдоль оси аргумента x. Своеобразие их поведения проявляется при попытке изменения масштаба аргумента, т.е. при переходе от y(x) к функции y(v) нового ар­гу­ментаv = k·x.

Рассмотрим сначала особенности поведения зависимостейy(·),не имеющихв своём составедельтообразных компонент. Если функцииy(x) и y(v) имеют совпадающую размерность,то никаких мер по нормировке значений принимать не требуется, а правило расчета доли величины Y, приходящейсяна произвольный интервал от до , возникает при интегрировании автоматически - путем очевидной замены переменных

,

(П1.0)

где, очевидно, и .

Классические примеры подобной нормировки можно найти, на­при­мер, в облас­ти спектрального анализа. Частотные характерис­тики могут выра­жаться функциями циклической часто­ты f, изме­ряемой в гер­цах, или функциями круговой частоты ω, измеряемой в радианах за секунду. Однако, вне зависимости от конкретного используемого аргумента значения характеристик сигналов и цепей остаются неизменными и лишь при интегрировании по частоте ω перед интегралом появляется нормировочный коэффициент «1 / 2π».

Если же замена аргумента сопровождается соответству­ющим из­ме­нением размерностирезультатов, то значения функции должны быть увеличены вkраз. Например, если плотность печати принтера составляет 600 точек на дюйм, то при пересчете к 1 метру, включающему 39,37 дюйма, плотность печати будет уже 23622 точек на метр, что соответствует соотношению между аргументами. В подобных случаях, очевидно, расчетная формула (П1.0) распадается на две независимые части, каждая из которых не требует поправочных коэффициентов

.

(П1.0)

Случай присутствия дельтообразных компонент:

Пусть теперь в составе зависимости y(x), имеется слагаемое видаY₀ · δ(x-x₀). Это означает, что доля величины Y, приходящейся на бесконечно малую окрестность точки x₀, составляетY₀. Очевидно, что в бесконечно малой окрестности точки v₀ = k·x₀ должна содержаться та же доля Y.

Если функции y(x) и y(v) дают результаты с совпадающей размерностью, то для расчета этой доли Y будет использоваться (П1.0), а значит для сохранения Y поправочные коэффициенты потребуется увеличить в k раз, т.е.

,

(П1.0)

где-часть зависимости, не содержащая дельтообразных компонент.

Если же замена аргумента сопровождается изменением размерности результатов, то в соответствии с (П1.0) корректи­ровка коэффициентов при дельта-функции не требуется

.

(П1.0)
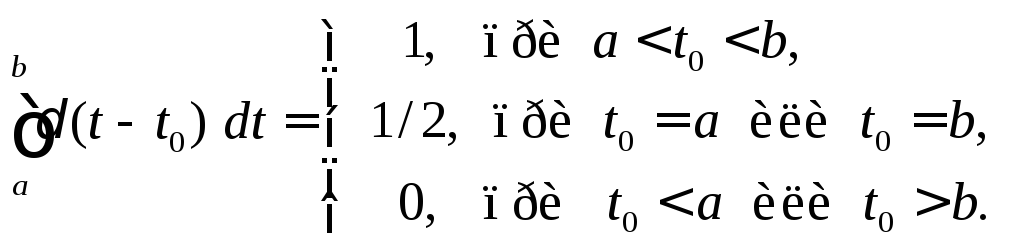