4. Плотность распределения вероятностей системы св

Плотность распределения вероятностей системы СВ характеризует вероятность наблюдения в опыте значений системы, принадлежащих бесконечно малой окрестности точки, задаваемой аргументами плотности вероятности. При сокращении размеров окрестности контрольной точки вероятность попадания в неё практически всегда стремится к нулю, поэтому для получения измеримых результатов уменьшающуюся вероятность (аналогично изложенному на с. 83) соотносят с уменьшающимися геометрическими размерами контролируемой области пространства. На основе ( 6 .0) можно показать, что для системы 2 случайных величин данное отношение стремится к значению смешанной производной 2-го порядка от ФРВ системы по каждому из её аргументов.

Итак, плотность распределения вероятностей системы 2 СВ численно определяетсясоотношением

(6.0)

Основные свойства плотности вероятности системы 2 СВ:

1. Плотность вероятности системы имеет размерность, обратную произведению размерности всех входящих в неё СВ и принимает лишь неотрицательные значения

,

(6.0)

т.е. если величины ξиη, к примеру, соответствуют координатам объекта, выраженным в метрах, то размерностью плотности вероятности будет «1/м²»; если же ξ – это некоторый ток, а η – какое-то напряжение, то размерностью функции будет «1/(А∙В)».

2. Для расчета вероятности наблюдения в опытах значений системы СВ, принадлежащих произвольной области простран­ства, достаточно проинтегрировать на множестве точек, образующих эту область. Если же контрольная область имеет прямолинейную форму, то расчетная формула приобретает вид

.

(6.0)

3. Если в область интегрирования из ( 6 .0) включить все возможные сочетания значений, то анализируемое пересечение требований становится достоверным событием и потому

.

(6.0)

Соотношение ( 6 .0) – это новый вариант свойства нормировки. С геометрических позиций интеграл ( 6 .0) определяет объем тела, заключенного между горизонтальной плоскостью и поверх­­ностью, форму которой задает анализируемая плотность вероятности. В результате, для любой системы 2 СВ объем тела, определяемого , обязан оставаться постоянным, строго равным единице.

4. С учетом определения ( 6 .0), правило расчета ФРВ по плотности вероятности системы СВ имеет вид

.

(6.0)

5. Наконец, для выделения из плотности вероятности системы закона распределения какой-то конкретной величины следует проинтегрировать по всем прочим переменным

; .

(6.0)

Пример 2: Найти функцию распределения вероятностей системы СВ, плотность вероятности которой определяется выражением .

Решение: Для решения задачи достаточно воспользоваться правилом ( 6 .0)

.

Примечание: Обратите внимание, что целью задачи было получение функции распределения вероятностей, т.е. не какого-то числа (константы), а правила, связывающего аргументы x₀ и y₀, с заранее неизвестным результатом .

5. Зависимость случайных величин и условные законы распределения составляющих системы св

Образующие систему случайные величины называются независимыми, если принятие одной из величин конкретного значения никак не сказывается на вероятности принятия в том же опыте тех или иных значений другой (другими) СВ.Для независимости величин ξ и η необходимо и достаточно, чтобы ФРВ системы можно было представить в виде произведения законов распределения величинξиη

,

(6.0)

В соответствии с определением ( 6 .0) для плотности вероятности системы условие независимости величин ξиηимеет аналогичный вид

.

(6.0)

Если же факт принятия величиной ξ конкретного значенияxизменяет вероятность принятия СВηзначенияy, тоξ и η являются зависимыми. Для работы с подобными величинами часто оказывается удобно использовать условные ФРВ и плотности вероятности. Знакомство с условными законами распределения разумно начать с анализа следующего предела

.

Проанализированная выше вероятность, определяющая ФРВ СВ η, вычисленную при условии, что принятое в опыте величиной ξ значение фактически известно, называется условной функцией распределениявеличиныη

(6.0)

Аналогично, условная плотность вероятности величины η, зависящей от величины ξ, определяется выражением

(6.0)

и характеризует возможность наблюдения значений СВ ηиз бесконечно малой окрестности аргументаyв тех опытах, где величинаξнаходилась в бесконечно малой окрестностиx.

Для условных плотностей вероятности тоже выполняется условие нормировки

,

(6.0)

а приведенные ниже выражения являются аналогами формулы полной вероятности

,	(6.0)
.	(6.0)

В итоге, аналогом формулы Байеса для непрерывных случайных величин ξиηможет служить правило

.

(6.0)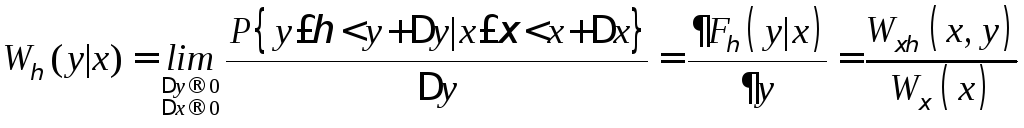