
- •Учебник подготовлен в рамках Инновационной образовательной программы
- •ISBN 978-5-7262-0821-3
- •5.1. Однокомпонентные диаграммы фазового равновесия,
- •5.2.1. Диаграмма с полной взаимной растворимостью
- •5.2.4. Диаграммы с наличием трехфазного равновесия
- •5.2.5. Диаграммы с эвтектическим и эвтектоидным
- •5.2.6. Диаграммы с монотектическим и монотектоидным
- •5.2.8. Диаграммы с перитектическим и перитектоидным
- •7.1. Физико-химические основы взаимодействия
- •7.1.4. Роль термодинамики и химической кинетики
- •7.2.3. Пленки на металлах как продукты химической
- •7.2.9. Формирование защитных жаростойких пленок
- •7.2.10. Влияние внешних и внутренних факторов
- •7.3.3. Механизм электрохимической коррозии. Работа
- •7.3.4. Гетерогенность поверхности и микрогальванические
- •7.3.7. Термодинамика процессов электрохимической
- •7.4.3. Влияние примесей в жидких металлах
- •7.4.4. Основные пути снижения взаимодействия
- •конструкционных материалов с жидкометаллическими
- •7.5. Защита от коррозии на стадии проектирования и разработки
- •Предисловие к тому 2
- •Глава 4. ТЕРМОДИНАМИКА В МАТЕРИАЛОВЕДЕНИИ
- •Введение.
- •4.1. Основные понятия термодинамики
- •4.2. Метод термодинамических потенциалов
- •4.3. Прикладная термохимия
- •4.4. Фазовые равновесия
- •4.5. Термодинамика растворов
- •4.6. Физическая химия неидеальных растворов
- •4.7. Термодинамическая теория диаграмм состояния
- •Список использованной литературы
- •Глава 5. ДИАГРАММЫ ФАЗОВОГО РАВНОВЕСИЯ
- •Введение
- •5.2.2. Диаграмма с расслоением твердого раствора
- •5.2.3. Диаграмма с наличием упорядочения
- •5.2.4. Диаграммы с наличием трехфазного равновесия
- •5.2.7. Диаграмма с метатектическим равновесием
- •5.2.9. Диаграмма с синтектическим равновесием
- •5.2.10. Диаграммы с промежуточными фазами
- •5.3. Диаграмма железо – углерод
- •5.4. Анализ сложных диаграмм фазового равновесия
- •Контрольные вопросы
- •Список использованной литературы
- •6.4. Закономерности сегрегации примесей
- •Контрольные вопросы
- •Список использованной литературы
- •Глава 7. СОВМЕСТИМОСТЬ И КОРРОЗИЯ МАТЕРИАЛОВ
- •7.1.1. Совместимость материалов со средой
- •7.1.2. Коррозия. Основные понятия и определения
- •7.1.3. Коррозионные проблемы
- •7.1.5. Классификация процессов коррозии
- •7.2. Химическая коррозия металлов
- •7.2.1. Химическая газовая коррозия
- •7.2.4. Состав и структура оксидов. Эпитаксия
- •7.2.5. Толщина и защитные свойства пленок
- •7.2.7. Механизм химической газовой коррозии
- •7.2.8. Оксидные пленки на поверхности железа
- •7.2.11. Химическая коррозия в газовых теплоносителях
- •7.3. Электрохимическая коррозия
- •7.3.1. Основные признаки и причины
- •7.3.2. Электролиты
- •7.3.6. Электродные потенциалы
- •7.3.8. Диаграммы Пурбе
- •7.3.9. Кинетика электрохимических процессов коррозии
- •7.3.10. Электрохимическая защита
- •7.4. Коррозия в жидкометаллических средах
- •7.4.1. Типы процессов
- •7.4.2. Растворение твердого металла в жидком
- •7.5. Защита от коррозии на стадии проектирования
- •7.5.1. Коррозия и вопросы конструирования
- •7.5.2. Выбор материалов и их совместимость
- •7.5.3. Выбор рациональной формы элементов
- •7.5.4. Учет влияния механических нагрузок
- •7.5.5. Рациональные способы сборки конструкций
- •Контрольные вопросы
- •Список использованной литературы

вместе. Если оставаться в пределах точности сделанных выше допущений, то для более полного описания температурной и концентрационной зависимости коэффициентов активности разумно объединить формулы (4.174) и (4.175):
ln(γA ) = (Ω − sT ) (1− xA )2 ; ln(γB ) = (Ω − sT ) (1− xB )2 . (4.176) RT RT
Данная модель растворов получила название квазирегулярных. В моделях квазирегулярных растворов сохраняют форму записи (4.163), но параметр взаимодействия считают линейно зависящим
от температуры: |
|
Ω = h – sT. |
(4.177) |
Физическая природа такой зависимости была раскрыта выше: h
– это энтальпийный вклад в неидеальность раствора, s – энтропийный. Феноменологические коэффициенты h и s определяются экспериментально.
4.7.Термодинамическая теория диаграмм состояния
4.7.1.Постановка задачи
Для получения представления об общем виде диаграмм состояния и его зависимости от знака и величины параметра взаимодействия Ω рассмотрим термодинамические законы равновесия в неидеальных системах. Для простоты ограничимся случаем регулярных бинарных растворов.
Главным из явных условий термодинамического равновесия в неидеальных системах остается равенство химических потенциалов компонентов в разных фазах. По аналогии с идеальными системами (см. выражение (4.111)), запишем условие равновесия твердой и жидкой фаз через парциальные молярные потенциалы Гиббса. Для этого, согласно рекомендации Льюиса, заменим в (4.111) концентрации на активности:
GAoS (T ) + RT ln(aAS ) |
= |
GAoL (T ) + RT ln(aAL ); |
(4.178) |
|
GBoS (T ) + RT ln(aBS ) |
= |
GBoL (T ) + RT ln(aBL ). |
||
|
||||
|
146 |
|
|
Для вычисления активностей согласно теории регулярных растворов имеем уравнения:
S |
S |
|
(1 |
− xS )2 Ω |
S |
|
|
||||
|
|
|
A |
|
|
|
; |
||||
aA = xA exp |
|
|
RT |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
S |
S |
|
|
|
S |
2 |
|
|
|
|
|
|
(1− xB ) |
|
ΩS |
|
|||||||
aB |
= xB exp |
|
|
|
|
|
|
; |
|||
|
|
RT |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
L |
L |
|
|
L |
2 |
|
|
|
|
|
(1− xA ) |
|
|
ΩL |
|||||
aA |
= xA exp |
|
|
|
|
|
|
; |
|
|
RT |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
L |
L |
|
|
L |
|
2 |
|
|
|
|
|
(1− xB ) |
|
ΩL |
|||||
aB |
= xB exp |
|
|
|
|
|
|
. |
|
|
RT |
|
|
|
|||||
|
|
|
|
|
|
|
|
||
(4.179)
(4.180)
Воспользовавшись справедливыми и для неидеальных систем условиями нормировки концентраций (4.110):
|
|
|
|
xAL + xBL = 1; |
xAS + xBS = 1, |
|
подставляя их в (4.179) вместе с (4.180) в (4.178), имеем: |
|
|||||
RT ln |
1− xBS |
+( GAoL (T) − GAoS (T)) = (xBS )2 ΩS −(xBL )2 ΩL ; |
|
|||
|
|
|
||||
|
1− xBliq |
|
|
(4.181) |
||
RT ln |
xBS |
+( |
GBoL (T) − GBoS (T))= (1− xBS )2 ΩS −(1− xBL )2 ΩL. |
|||
|
|
|||||
|
xBL |
|
|
|
||
Как и в случае идеальных систем, получено два уравнения относительно трех неизвестных величин: xBS , xBL , Т. Следовательно, и в
неидеальных системах равновесие жидкость–твердое будет на диаграмме состояния в координатах {х,Т} описываться двумя линиями: ликвидусом и солидусом. Перепишем (4.112) в том же виде, что и (4.181), более типичном для компьютерных расчетов:
RT ln |
1− xBS |
+ ( GAoL (T ) − GAoS (T ))= 0; |
||||
|
1− xBL |
|
(4.182) |
|||
RT ln |
xBS |
|
+ ( |
GBoL (T ) − GBoS (T ))= 0. |
||
xBL |
||||||
|
|
|
|
|||
Как видим, в отличие от системы (4.182) правые части у (4.181) являются не нулем, а алгебраическими функциями от концентраций и зависят так же от параметров взаимодействия в обеих фазах. Поскольку в левой части системы (4.181) стоят логарифмические функции, составляющие ее уравнения трансцендентны. Следовательно, сама система для описания равновесия неидеальных растворов не только не имеет аналитических решений, но и при произвольно заданной температуре Т вообще стоит вопрос о сущест-
147

вовании и числе ее решений относительно xBS , xBL в положительных действительных числах, меньших единицы.
4.7.2. Основы графической термодинамики
До появления компьютерной техники для расчета диаграмм состояния применялись методы графической термодинамики. Она создана еще Гиббсом и основана на взаимосвязи интегральных и молярных термодинамических характеристик растворов. С развитием компьютерной техники для этой цели стало проще и эффективней сразу использовать численные методы решения системы уравнений (4.181) или эквивалентных ей для других моделей растворов. Однако графическая термодинамика в силу ее наглядности не потеряла своего значения и сегодня. Мы будем использовать графические методы не для строгого расчета, а для иллюстрации теоретических принципов, отражающих взаимоотношения равновесных фаз.
Основой методов графической термодинамики является совместное рассмотрение кривых концентрационной зависимости молярных потенциалов Гиббса для двух растворов, находящихся в равновесии. Зависимость потенциала Гиббса Gm одного моля всего раствора от концентрации x второго компонента В, согласно (4.98), описывается формулой:
Gm(р, Т, x) = x· G В (р, Т, x) + xА· G А(р, Т, x) =
|
|
|
|
|
|
|
|
|
|
|
|
= x· G В (р, Т, x) + (1– x)· G А(р, Т, x). |
(4.183) |
||||||||||
Поскольку |
|
|
|
|
|
||||||
|
|
|
|
А(р, Т, x) = |
GAo |
(р, Т) + RTln(aA), |
|
||||
G |
|
||||||||||
|
|
В(р, Т, x) = |
GBo |
(р, Т) + RTln(aB), |
|
||||||
|
G |
|
|||||||||
а для любого чистого компонента его активность равна единице, понятно, что кривая, соответствующая уравнению (4.183), отсекает на ординатах x = 0 (aA = 1) и x = 1 (aB = 1) величины:
Gm(р,Т, x=0) = |
G |
|
А (р,Т, x=0) = |
GAo (р,Т) + RTln(1) = |
GAo |
(р,Т); |
Gm(р,Т, x=1) = |
|
В (р,Т, x=1) = |
GBo (р,Т) + RTln(1) = |
GBo |
(р,Т), |
|
G |
||||||
|
148 |
|
|
|||

равные значениям стандартных потенциалов чистых компонентов
А и В.
Далее, частная производная от выражения (4.183) по х, равная:
∂ |
G |
m |
(x) |
|
|
|
|
|
|
= G В(р,Т, x) – G А(р,Т, x) = tg(α(x)), (4.184) |
|||||||||
|
|
|
|||||||
|
∂x |
p,T |
|||||||
по смыслу есть тангенс угла наклона касательной к кривой концентрационной зависимости молярного потенциала Гиббса раствора. Записывая само уравнение этой касательной f(x) в произвольной
точке с концентрацией x*B как уравнение прямой в отрезках:
f(x) = G А(р,Т, x*B )+x ·[ΔG В(р,Т, x*B ) – G А(р,Т, x*B )] (4.185)
видим, что касательная отсекает на ординатах x = 0 и x = 1 значения парциальных потенциалов Гиббса компонентов в этом рас-
творе x*B :
f(0) = |
G |
А(р,Т, xB* ); f(1) = |
G |
В(р,Т, xB* ). |
(4.186) |
Поскольку равенство именно парциальных энергий Гиббса всех одноименных компонентов в разных фазах является условием равновесия этих фаз, то из (4.185) и (4.186) следует, что графической интерпретацией этого равенства является наличие общей касательной у кривых концентрационной зависимости молярных потенциалов Гиббса растворов, образующих разные фазы. Визуальный поиск таких общих касательных и составляет сущность графической термодинамики.
Поясним сказанное выше численным расчетом простейшей бинарной системы, в которой оба раствора являются идеальными. Для иллюстрации порядка численных значений реальных величин за термохимические данные для компонента А примем свойства тантала; данные для компонента В пусть соответствуют β- цирконию. Исходные данные для чистых реальных компонентов при разных температурах приведены в табл. 4.5.
На рис. 4.24 для выбранной условной (виртуальной) системы представлены расчеты интегральной молярной энергии Гиббса Gm по модели идеального твердого раствора при температуре 2500 К. Заметим, что в действительности в системе Ta–Zr наблюдается су-
149

щественное положительное отклонение от идеальности в твердой фазе. Поэтому приводимые в данном разделе расчетные термодинамические характеристики условных растворов носят чисто демонстрационный характер. Они только показывают порядки реальных численных значений, качественно и количественно иллюстрируя вид графического отображения различных зависимостей.
|
|
|
|
|
|
|
|
Таблица 4.5 |
||
|
Некоторые свойства тантала и циркония |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Пара- |
Тплавл, |
|
Энергия Гиббса |
Go, |
кДж/моль |
|
|||
Ме- |
метр |
|
|
|
|
|
|
|
||
2000 К |
2500 К |
|
3500 К |
|||||||
талл |
решетки, |
К |
тв |
ж |
тв |
ж |
|
тв |
|
ж |
|
нм |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Та |
0,3303 |
3269 |
–140 |
–128 |
– 189 |
– 181 |
|
–297 |
|
–299 |
|
|
|
|
|
|
|
|
|
|
|
Zr |
0,3616 |
2125 |
–142 |
–141 |
– 193 |
– 196 |
|
–309 |
|
–319 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.24. Энергетические характеристики:
1 – Gm виртуального твердого раствора Ta-Zr, принятого за идеальный; 2 – касательная к кривой 1
при х = 0,5
Рис. 4.24, прежде всего, иллюстрирует тот факт, что обсуждаемая кривая несимметрична – касательная в точке x = 0,5 не является горизонталью. Численные значения рассчитанных парциальных мольных величин (для х = 0,5) составляют:
GAs = –203,5 кДж/моль; GBs = –207,5 кДж/моль.
Далее, из рисунка 4.27 видно, что концентрационная зависимость молярных потенциалов Гиббса идеальных растворов описывается вогнутыми кривыми с единственным минимумом. Данный
150
результат, полученный из численных расчетов, можно доказать строго аналитически, исследуя выражение (4.184), записанное для идеального раствора. Для этого достаточно показать, что первая
∂ |
G |
m |
(x) |
непрерывна, монотонна и меняет знак |
производная |
|
|
||
|
∂x |
p,T |
|
|
на отрезке [0;1]. Из-за непрерывности согласно теореме Ролля она обязательно имеет одно (а из-за монотонности – только одно) нулевое значение. Сама функция в этой точке имеет экстремум. Пока-
зав, что вторая производная |
|
∂2 |
Gm (x) |
всюду положительна, |
|
|
|
∂x2 |
|
||
|
|
|
|
|
|
|
|
|
|
p,T |
|
докажем, что экстремум есть минимум. Сразу заметим, что вывод о единственности экстремума на неидеальные растворы не распространяется. Для них кривая концентрационной зависимости молярных энергий Гиббса может иметь два и более минимумов и максимумов.
На рис. 4.25 приведены зависимости энергий Гиббса для двух фаз виртуальной бинарной системы – твердого и жидкого растворов. Как и ранее, идеальными считаются оба раствора. Расчеты выполнены при трех разных температурах: высокой, средней и относительно низкой.
Рис. 4.25,а показывает, что если температура системы ниже температуры плавления более легкоплавкого компонента, то кривая концентрационной зависимости энергии Гиббса для твердой фазы – идеального раствора не пересекает такую кривую для жидкости. Это означает, что обсуждаемые кривые не имеют общих касательных на отрезке [0;1], и система (4.112) не имеет решений, т.е., идеальные твердая и жидкая фазы при этих температурах не могут быть в равновесии. Поскольку кривая концентрационной зависимости энергии Гиббса для твердой фазы лежит здесь всегда ниже такой кривой для жидкости, то равновесной здесь будет однофазная среда – твердый раствор.Аналогичный вывод об отсутствии возможности равновесия идеальных твердой и жидкой фаз при температурах выше температуры плавления более тугоплавкого компонента следует из рис. 4.25,в. Действительно, при высоких
151

температурах концентрационная кривая Gm(х) для идеального твердого раствора идет уже всегда выше кривой для такого же жидкого, т.е. равновесной здесь будет однофазная жидкая среда.
|
|
а |
б |
Рис. 4.25. Кривые концентрационной зависимости молярных потенциалов Гиббса (в кДж/моль) для условных идеальных твёрдого и жидкого растворов Ta–Zr при разных температурах:
а – ниже температуры плавления любого компонента (Т = 2500 К); б – между температурами плавления компонентов (Т = 3000 К);
в – выше температуры плавления любого компонента (Т = 3500 К)
в
На рис. 4.25,б и 4.26 представлен случай, когда температура системы находится между температур плавления компонентов А и В.
152
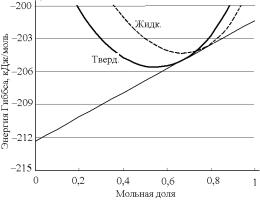
Рис. 4.26. Энергетические характеристики Gm твердого и жидкого растворов Ta–Zr, принятых за идеальные, и общая касательная
Как видно, здесь кривые концентрационной зависимости энергий Гиббса для твердой и жидкой фаз пересекаются, причем в одной точке. Сама точка пересечения, как и точки минимумов, не несет физического смысла. Но ее наличие говорит о существовании одной общей касательной к этим двум кривым, причем точки касания – решения системы – лежат слева и справа от точки пересечения. Поэтому значение х в точке пересечения можно использовать в качестве начального приближения для поиска решения численными методами. Заметим так же, что в общем случае число точек пересечения кривых показывает число общих касательных, т.е. число действительных решений системы (4.181). Такая наглядность
–одно из достоинств методов графической термодинамики.
Вслучае, когда температура системы находится между значениями температур плавления компонентов А и В, кривые концентрационной зависимости энергий Гиббса для твердой и жидкой фаз пересекаются в единственной точке. Следовательно, они имеют только одну общую касательную (см. рис. 4.26), а система уравнений (4.112) – единственное решение. Под единственностью решения понимается то, что каждой температуре соответствует только по одной точке на кривых солидуса и ликвидуса. Для варианта, представленного на рис. 4.26, расчет показывает, что в равновесии
находятся: твердый раствор состава 0,67; жидкий раствор состава 0,78. При этом:
153
GAS = GAL = –212,3 кДж/моль;
GBS = GBL = –201,5 кДж/моль.
Диаграмма состояния в обсуждаемом варианте имеет вид, показанный на рис. 4.27,а, линия ликвидуса выгнута вверх, а солидуса – вниз. Заметим, что для идеальных растворов все выводы о существовании, единственности и области существования решений, сделанные в данном параграфе на основании численных расчетов и графиков, представленных на рис. 4.25, были уже доказаны в общем виде в п. 4.5.5.
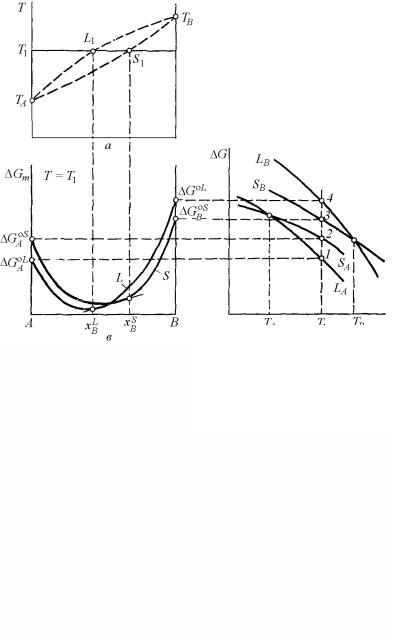
На рис. 4.27 показана принципиальная схема установления методами графической термодинамики положения координат фигуративных точек, соответствующих двухфазному равновесию в двухкомпонентной системе, где обе фазы являются идеальными растворами. В качестве примера определим составы равновесных фаз при температуре Т1, которая занимает некоторое промежуточное положение между температурами ТА и ТВ .
Рис. 4.27. Принципиальная схема установления фиксированного положения координат фигуративных точек, соответствующих равновесно сосуществующим фазам
в двухкомпонентной двухфазной системе
154
Рис. 4.27,а представляет плоскость Т-х, в которой строится диаграмма состояния. На ней сразу отмечается то, что известно до расчетов: температуры плавления компонентов ТА и ТВ. При температурах плавления чистых компонентов – граничных температурах, где решение еще существует – точки пересечения и касания совпадают. Это означает, что точки ликвидуса и солидуса сливаются, соответствуя чистым компонентам.
Далее, рассчитываются и строятся (рис. 4.27,б) четыре кривые температурной зависимости изобарно-изотермического потенциала Гиббса твердых и жидких фаз для обоих чистых компонентов А и В. Вертикальной линией отмечается положение заданной температуры Т1. При пересечении указанных кривых с вертикалью Т1 на рис. 4.27,б появляются точки, определяющие значения потенциалов Гиббса:
• |
1, |
2 |
– соответственно жидкой |
GAoL |
и твердой |
GAoS фаз |
|
|
|
компонента А; |
|
|
|
• |
3, |
4 |
– соответственно твердой |
GAoS |
и жидкой |
GBoL фаз |
компонента В.
Значения потенциалов в этих точках переносятся горизонталями на ординаты плоскости рис. 4.27,в, на которой будут представлены кривые концентрационной зависимости энергий Гиббса твердой и
жидкой фаз растворов. Точки GAoL и GAoS , GAoS и GBoL являют-
ся крайними для соответствующих кривых.
По уравнениям (4.183) рассчитываются концентрационные зависимости энергий Гиббса жидкого и твердого растворов и строят-
ся кривые, соединяющие попарно точки GAoL и GBoL , GAoS и
GAoS . В итоге получаются две пересекающиеся линии (см. рис. 4.27,в). Проводя к ним общую касательную, по абсциссам точек касания определяются составы жидкой xBL и твердой xBS фаз, рав-
новесные при заданной температуре Т1. Проектируя эти составы на горизонталь Т1 на рис. 4.27,а, определяем положения фигуративных точек L1 и S1, отмечающих равновесное состояние жидкой и твердой фаз уже в координатах Т–х, т.е. на диаграмме состояния.
155
Повторяя ход рассуждений для любой другой температуры в интервале между ТА и TВ, получаем для каждой из них соответствующую пару сопряженных точек. Соединяя на рис. 4.27,а общими кривыми все Li и Si, и замыкая их в точках ТА и TВ, получаем собственно фазовую диаграмму.
Следует отметить, что рассмотренный вариант фазовой диаграммы включает типичное двухфазное равновесие с двумя растворами, которое является характерным абсолютно для всех других систем и фигурирует в них в качестве обязательного элемента. В данной книге этот случай фазового равновесия в основном связывается с взаимными переходами жидкость–твердое, обозначаемыми на диаграммах состояния линиями ликвидуса и солидуса. Но все выводы, сделанные здесь и ниже, распространяются на любые другие виды фазовых равновесий, например, жидкость–пар или
твердое–твердое.
4.7.3. Неидеальные системы с неограниченной растворимостью
Система, представленная на рис. 4.27,а, является простейшей с двумя непрерывными растворами, ограниченными на диаграмме состояния монотонными линиями равновесия (ликвидусом и солидусом) во всем диапазоне концентраций.
Рассмотрим теперь, как методами графической термодинамики можно определять существенные особенности диаграмм состояния, на примере более сложных, неидеальных систем с неограниченной растворимостью, подчиняющихся законам регулярных растворов. Причем в данном разделе будем рассматривать растворы, в которых параметр взаимодействия Ω разнородных компонентов не слишком велик:
|Ω| ≤ RT.
В соответствии с логикой графической термодинамики, необходимо изучать влияние неидеальности на характер концентрационной зависимости интегральных молярных энергий Гиббса Gm двух сосуществующих растворов. Согласно определениям интегральных и избыточных характеристик растворов, из п. 4.6.5 имеем:
156
Gm = Gmid + Gизб = Gmid + ( Hизб – T· Sизб). |
|
|
Для регулярных растворов |
|
|
Sизб = 0, а |
Низб = x(1–x)Ω. |
|
Тогда имеем: |
|
|
Gm = |
Gmid + x(1–x)Ω, |
(4.187) |
т.е. различие концентрационных зависимостей молярных энергий Гиббса регулярного и идеального растворов не зависит от температуры и полностью определяется величиной параметра взаимодействия Ω. При Ω > 0 прогиб на графике соответствующей кривой уменьшается, при Ω < 0 – увеличивается по параболическому закону. Заметим так же, что крайние точки кривой, соответствующие чистым компонентам, остаются на месте.
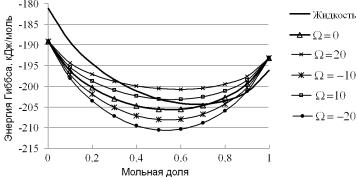
Проиллюстрируем сказанное численным примером – мысленным экспериментом, в котором будем изменять величину параметра взаимодействия компонентов одного из растворов. Для простоты и большей наглядности примем, что жидкий раствор идеален (Ωliq = 0), а твердый будет регулярным (Ωs ≠ 0). Результаты расчетов той же демонстрационной системы, что и ранее, но для разных значений параметра взаимодействия в твердом растворе приведены на рис. 4.28.
Рис. 4.28. Концентрационные зависимости молярных энергий Гиббса Gm идеального жидкого и регулярных твердых растворов при разных значениях параметра взаимодействия Ω в кДж/моль. Температура системы лежит между температур плавления чистых компонентов Ta и Zr
157
Как видно из рисунка, если температура системы находится между температурами плавления чистых компонентов, при измене-
нии параметра взаимодействия кривые GL |
(x) для жидкости и |
m |
|
GmS (x) для твердого по-прежнему пересекаются, и только в одной
точке. Эта точка – своя для каждого значения параметра взаимодействия. Следовательно, обсуждаемые кривые по-прежнему имеют только одну общую касательную, и в каждом случае есть только одно, но уже отличное от случая идеальных растворов решение. По-другому, можно сказать, что если температура системы находится между температурами плавления чистых компонентов, то для любой неидеальной системы на диаграмме состояния в этом температурном интервале имеется только по одной линии ликвидуса и солидуса.
Заметим теперь, что из рис. 4.28 видно, что, при росте величины положительного параметра взаимодействия, точки пересечения, а с
ними и точки с общей касательной на кривых GS |
(x) , |
GL |
(x), |
m |
|
m |
|
смещаются в сторону более тугоплавкого компонента. Это означает, что при увеличении параметра взаимодействия жидкая фаза появляется при более низкой температуре – линии ликвидуса и солидуса прогибаются вниз относительно их положения для идеального раствора.
Аналогично, при росте (по модулю) величины отрицательного
параметра взаимодействия точки пересечения кривых GS |
(x), |
m |
|
GmL (x) смещаются в сторону более легкоплавкого компонента.
При этом линии ликвидуса и солидуса прогибаются вверх относительно их положения для идеального раствора. Но в определенных пределах небольших по модулю величин параметра взаимодействия диаграмма состояния останется «сигарой», правда, с искаженным относительно идеальной системой формой.
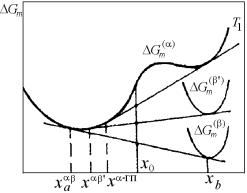
При большем отклонении от идеальности, кривые ликвидуса и солидуса на соответствующей диаграмме состояния коснутся друг друга и приобретут общую точку. В случае положительного отклонения это будет минимум, отрицательного – максимум. Общий вид фазовых диаграмм этого типа показан на рис. 4.29.
158
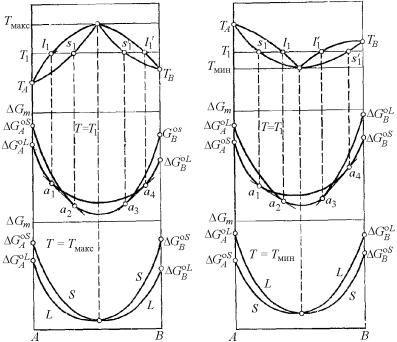
Рис. 4.29. Обоснование диаграмм состояния двухкомпонентной системы с непрерывным рядом твердых и жидких растворов при наличии общей точки на кривых ликвидуса и солидуса:
а – максимума (Ω < 0); б – минимума (Ω > 0)
Как видно, неограниченная растворимость и здесь еще может сохраняться. Термодинамическое обоснование формы этих диаграмм с помощью кривых концентрационной зависимости изобар- но-изотермических потенциалов аналогично приведенному выше. Однако в температурном интервале между точками максимума (или минимума) и соответственно ближайшей температурой плавления одного из компонентов изотерма T1 (рис. 4.29) показывает наличие двух различных двухфазных равновесий по концентрации
– левее и правее точки экстремума. Каждая пара сопряженных фаз при данной температуре характеризуется собственным условием фазового равновесия и, следовательно, может быть интерпретирована графически при помощи соответствующих кривых концен-
159
трационной зависимости изобарно-изотермического потенциала, к которым проведена общая касательная.
При относительном расположении кривых GmS (x) и GmL (x),
показанном на рис. 4.29,а, проведением общих касательных a1–a2 и a3–a4 фиксируются составы фаз, находящихся в равновесии при
T1. При Тмакс кривые зависимости GS |
(x) и |
GL |
(x) касаются друг |
m |
|
m |
|
друга в точке, концентрация в которой отвечает общему максимуму на кривых ликвидуса и солидуса. При этом во всем интервале
концентраций кривая GmL (x) располагается непременно ниже кривой GmS (x), что подчеркивает устойчивость при этой температуре
жидкой фазы и неустойчивость твердой.
В случае диаграммы с минимумом на кривых ликвидуса и солидуса (рис. 4.29,б) при температуре T1 так же имеются два самостоятельных двухфазных равновесия. Проводя точно так же две общие касательные a1–a2 и a3–a4 к кривым концентрационной зависимости свободной энергии Гиббса твердой и жидкой фаз, фиксируем составы равновесных фаз, определяемые концами коннод s1 −l1 и s1′ −l1′ .
При температуре минимума Тмин (или максимума Тмакс) на кри-
вых ликвидуса и солидуса кривые GS |
(x) и |
GL |
(x) касаются друг |
m |
|
m |
|
друга (см. рис. 4.29, нижние графики) в точке, отвечающей по концентрации составу минимума (максимума) при непременном относительно более низком расположении одной из кривых во всем интервале составов в связи. В точках максимума и минимума составы жидкой и твердой фаз одинаковы, т. е.
x(L) = x(S ) . |
(4.188) |
Выражение (4.188) является дополнительным условием, снижающим вариантность системы в данной точке на единицу. Поэтому в точке максимума или минимума для изобарического сечения системы равновесие должно быть нонвариантным, и сплавы, отвечающие составу экстремальных точек на рис. 4.29, ведут себя как однокомпонентные системы. Например, такие сплавы имеют определенную температуру плавления.
160

4.8. Системы с положительным отклонением от идеальности
В данном параграфе будем рассматривать системы с положительным отклонением от идеальности (Ω > 0), а именно случаи,
когда εАВ идет в ту же сторону, что и εAA εBB относительно
½εАА·εВВ. Этот вариант наиболее часто встречается на практике, так как законы взаимодействия атомов металлов в твердых растворах качественно примерно одинаковы, хотя и отличаются количественно.
4.8.1. Распад твердых растворов
Заметим, что на отклонение свойств раствора от идеального влияет не столько сам параметр взаимодействия Ω, сколько величина Ω/RT, входящая в выражение для коэффициента активности γ. Действительно, для регулярных растворов, согласно (4.163), имеем:
γ = |
|
Ω |
(1− x)2 |
|
|
exp |
|
, |
|||
RT |
|||||
|
|
|
|
где х – мольная доля второго компонента.
Отсюда видно, что при понижении температуры (увеличении Ω/RT) коэффициент активности, а с ним и неидеальность любого раствора увеличивается (для иллюстрации см. рис. 4.22).
Это приводит к проявлению важного физического явления в сплавах. Из экспериментальных данных известно, что в системах с параметром взаимодействия Ω > 0 и неограниченной растворимостью при высоких температурах, при понижении температуры наблюдается переход однофазной системы – гомогенного твердого раствора определенной концентрации – в двухфазную смесь двух твердых раствора разных составов, т.е., двухфазное состояние в виде механической смеси становится для данной системы при некоторых условиях более термодинамически выгодным, чем однофазное в виде однородного раствора. На практике это проявляется в том, что при медленном охлаждении сплава, или при изотермической выдержке (старении) закаленного неравновесного пересы-
161

щенного сплава происходит распад (расслоение) исходного раствора на два с разными составами.
Поясним физическую природу данного факта. В любом растворе происходят флуктуации состава – самопроизвольное отклонение от случайного распределения атомов А и В по кристаллической решетке: в кристалле образуются кластеры (микрообласти) с преимущественным содержанием или атомов сорта А, или атомов сорта В. При положительных Ω, при условии εAB > 1/2(εAA+ εBB), это приводит к уменьшению энергии системы. Следовательно, микрообласти, обогащенные как компонентом А, так и В, являются термодинамически стабильными, и их существование фиксируется. Более того, они с течением времени из-за диффузионных процессов срастаются в макроскопические области, образующие самостоятельные фазы. Так происходит распад твердого или расслоение жидкого раствора.
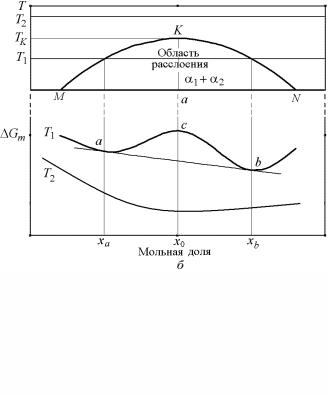
На диаграмме состояния распад раствора отражается в появлении на ней линии с максимумом – кривой (купола) расслоения. Это показано на рис. 4.30 на примере реальной системы Ta–Zr, где имеется сильно деформированная двойная «сигара» с минимумом и хорошо выраженный купол расслоения.
Рис. 4.30. Реальная диаграмма состояния системы сплавов
Ta–Zr
162

В п. 4.7.2 было показано, что для идеального раствора кривая зависимости от концентрации интегральной энергии Гиббса G°m (x) имеет только один минимум; она вогнута в каждой точке на всем интервале концентраций (0; 1), что качественно и количественно отражено на рис. 4.24–4.29. Это означает, что для идеального раствора равновесный состав всегда единственный, и в идеальной системе никакого распада растворов быть не может.
Исследуем термодинамику простейшего явления распада однофазного твердого раствора на два изоморфных по реакции
α→ α1 + α2.
Сиспользованием понятия избыточных термодинамических ве-
личин (см. п. 4.6.1), энергия Гиббса для реальных растворов в общем случае формально описывается уравнением:
Gm (T , x)= Gom (T , x) + Gmизб(T , x) . |
(4.189) |
|
Избыточная составляющая энергии Гиббса |
Gmизб |
в теории регу- |
лярных растворов равна избыточной энтальпии |
H mизб(x) , не зави- |
|
сящей от температуры. Для одного моля раствора из (4.157) имеем:
Gизбm (x) = H избm (x) =(1− x) x Ω.
При Ω > 0 избыточная энергия Гиббса раствора как функция концентрации имеет выпуклость вверх (парабола ветвями вниз на рис. 4.21). При высоких температурах, когда выполняется условие
Gизбm (x) = H избm (x) << Gom (T , x) ,
из (4.189) имеем
Gm (T , x) ≈ Gom (T , x).
Следовательно, при высоких температурах регулярный раствор ведет себя как идеальный: однофазная система устойчива, распада твердого раствора не происходит.
С понижением температуры интегральная энергия Гиббса G°m уменьшается по модулю. Тем самым, относительный вклад неидеальности в общую энергию системы увеличивается с уменьшением температуры. При температурах ниже некоторой критической ТK, когда начинает выполняться условие:
163
H mизб(x) ≈ Gom (T , x) ,
вклад неидеальности становится заметным, и концентрационная зависимость Gm(x) регулярного раствора приобретает вид кривой с двумя минимумами и одним максимумом (рис. 4.31). На ней обязательно существуют две точки a, b, через которые проходит общая касательная.
Рис. 4.31. Купол расслоения на (Т, х) диаграмме состояния (а) и характер концентрационной зависимости (б) изобарно-изотермического потенциала при разных температурах (Т2>T1), и, соответственно, при малых и больших значениях Ω/RT
Это является графическим отражением выполнения условия термодинамического равновесия в форме равенства молярных парциальных потенциалов Гиббса компонентов для двух растворов различных составов. Физически это означает, что устойчивой становится двухфазная система с двумя растворами из одних и тех же компонентов, но двух разных составов. Действительно, на участке кривой acb свободная энергия раствора больше, чем энергия механической смеси двух фаз составов xa и xb, описываемой прямой ab. Значит, участок, расположенный выше единственной возможной
164
касательной ab, относится к твердым растворам c составами, неустойчивыми при температуре Т1 и поэтому распадающимся по квазихимической реакции α → α1 + α2 на смесь из двух фаз с разными
составами xa и xb .
Тем самым доказана теорема: при больших положительных отклонениях от равновесия из-за наличия двух минимумов на кривой концентрационной зависимости интегральной энергии раствора одинаковые парциальные энергии Гиббса для каждого из компонентов в обеих твердых фазах регулярного раствора реализуются при двух и только двух разных составах.
Заметим, что ω-образная гладкая форма графика функции Gm(x) присуща сплавам, компоненты которого имеют одинаковую кристаллическую решетку в чистом состоянии. Заметим так же, что эти равновесные составы не соответствуют точкам минимума на концентрационной зависимости интегральной энергии Гиббса.
Определение составов равновесных фаз (купол в верхней части рис. 4.31,а – кривая расслоения) графическими приемами сводится к проведению общей касательной ab к кривой концентрационной зависимости изобарно-изотермического потенциала и постановке соответствующих точек на Т–х диаграмме.
Рассмотрим явление более подробно математически. Подставляя выражение (4.123):
|
|
|
|
(T , х) = |
Go(T ) + RT ln[a (T , х)] |
|
|
|||
G |
|
|
||||||||
|
|
|
i |
i |
|
|
i |
|
|
|
в (4.101): |
|
|
|
|
|
|
||||
|
|
|
= |
|
|
|
|
|||
Gi (T , P, x1,..., xi .xn )I |
Gi (T , P, x1,..., xi .xn )II |
|
||||||||
имеем в нашем частном случае: |
|
|
|
|
|
|
||||
|
GAos (T ) + RT ln(aAα1 ) |
= |
GAos (T ) + RT ln(aαA2 ); |
(4.190) |
||||||
|
GBos (T ) + RT ln(aBα1 ) |
= |
GBos (T ) + RT ln(aBα |
2 ). |
||||||
|
|
|||||||||
Особенностью этих уравнений для каждого компонента является то, что и в правой, и в левой частях у них стоят потенциалы Гиббса G° одних и тех же чистых веществ. Отсюда получаем специфическое условие фазового равновесия растворов в изоморфном состоянии, а именно равенство активностей компонентов в разных фазах:
aαA1 = aAα2 ; |
aBα1 = aBα2 . |
(4.191) |
165
На рис. 4.23 были представлены зависимости активности аВ от концентрации х, рассчитанные для разных температур (разных Ω/RT) по модели регулярного раствора с положительным отклонением от идеальности по формуле, вытекающей из (4.167):
|
Ω |
(1− x)2 |
|
|
||
aB = |
x exp |
|
. |
(4.192) |
||
RT |
||||||
|
|
|
|
|
||
Заметим, что уменьшению температуры (увеличению отношения Ω/RT) соответствует возрастание отклонения системы от идеальности – активности а все более отличаются от концентраций х (соответствующие кривые на рис. 4.23 лежат все более высоко). Но, кроме того, с уменьшением температуры меняется и качественный вид обсуждаемых кривых. Действительно, при высоких температурах кривые монотонны, каждому значению активности соответствует единственное значение концентрации. При более низких температурах, начиная с некоторой критической температуры ТК, кривые имеют максимум, минимум и точку перегиба. Здесь одному значению активности соответствуют целых три концентрации, но, как следует из (4.191), физический смысл имеют только два.
Рассмотрим выражение (4.192) как уравнение относительно неизвестной концентрации х. Поскольку оно трансцендентно, то число его решений не определено и зависит от соотношения численных значений величин аВ и Ω/RT. При больших температурах (Ω/RT ≤ 2) решение единственно и соответствует единственному составу раствора. При низких температурах (Ω/RT > 2) формальных решений у уравнения (4.190) становится сразу три. Два из них соответствуют двум реальным растворам разных составов, находящимся в термодинамическом равновесии между собой; третье не имеет физического смысла. Для вычисления равновесных концентраций в регулярных растворах из (4.191) имеем:
|
α |
|
(1− xα1 )2 Ω |
|
α |
|
|
(1− xα2 |
)2 Ω |
|
||
x |
1 |
|
|
|
= x |
|
2 |
|
|
|
|
= aB ; (4.193) |
|
exp |
RT |
|
|
|
exp |
RT |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
где аВ – пока неизвестное значение равновесной активности.
Из структуры уравнений (4.193) сразу видно тривиальное решение: х = 0,5. Именно оно не имеет физического смысла, но позволя-
166

ет легко найти два других действительных. Подставляя в (4.193) решение х = 0,5, получаем численное значение равновесной активности:
aB =0,5 |
|
0,25 Ω |
||
exp |
|
|
||
RT |
||||
|
|
|
||
и уже конкретное уравнение для вычисления двух реальных значений концентраций xα1 , xα2 :
|
(1− x) |
2 |
Ω |
|
|
|
|
|
|
= aB . |
(4.194) |
||
x exp |
RT |
|
|
|
||
|
|
|
|
|
|
Данное уравнение не имеет аналитического решения, но легко решается численно. Исходя из вида графика функции аВ(х), представленного на рис. 4.31, как простейший можно предложить
метод простых итераций. Для нахождения xα1 за начальное
приближение следует взять x0 = 0; для нахождения xα2 принять x0 = 1.Найдем теперь координаты (TK, xK) критической точки K – максимума на кривой расслоения рис. 4.31, ниже температуры которой только и начинается распад твердых растворов определенных составов. Поскольку аналитического выражения для кривой расслоения не получено, воспользуемся тем фактом, что, как видно из рис. 4.31, на графике аВ(х) имеется точка перегиба. Заметим, что с увеличением температуры действительные решения xα1 , xα2 уравне-
ния (4.194), а так же точки максимума и минимума на кривой аВ(х) стягиваются к одному и тому же тривиальному х = 0,5, лежащему на точке перегиба, которое и есть абсцисса хK критической точки.
Следовательно, в этой точке не только вторая ∂2a2B , но и первая
∂x
∂∂axB производные равны нулю. Поэтому критическую температу-
ру определим из условия:
∂aB (T , x) |
|
∂ |
|
|
|
(1 − xK )2 |
Ω |
|
|
|
|
|
|
||||||
|
= |
|
x |
K |
exp |
|
|
|
= |
|
|
|
|
||||||
∂x |
TK ,xK |
∂x |
|
|
RTK |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
||||||
167
|
(1− xK ) |
2 |
Ω |
|
|
(1− xK ) |
2 |
Ω |
|
|
|
|
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
RT |
|
|
RT |
|
|
− |
2(1− xK )RT |
= 0. |
|||||||||
= exp |
|
|
|
+ xK exp |
|
|
|
|
|
||||||||
|
K |
|
|
|
|
K |
|
|
|
|
|
|
|
|
K |
|
|
Подставляя в это выражение значение хK =0,5 имеем: |
|
|
|||||||||||||||
|
|
|
Ω |
|
=2 |
или |
|
|
|
T |
= |
Ω |
. |
|
(4.195) |
||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
RTK |
|
|
|
|
|
K |
|
|
2R |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отсюда следует, что теоретически все системы с положительными значениями Ω (или, что то же, при HM > 0) должны иметь купол расслоения. Экспериментально это не всегда наблюдается, поскольку при небольших значениях HM критическая температура расслоения настолько мала, что из-за малых скоростей диффузии на низкотемпературных участках диаграммы состояния однородный твердый раствор будет существовать бесконечно долго как метастабильный.
Численное исследование (4.194) показывает, что в модели регулярных растворов кривая расслоения имеет ось симметрии при хK = = 0,5. В действительности этот случай практически никогда не встречается – обычно кривая расслоения асимметрична и не является параболой. Это означает, что модель регулярного раствора при больших положительных отклонениях от идеальности не работает. Действительно, модель регулярных растворов построена на предположении о случайном распределении всех сортов атомов по кристаллической решетке. При больших положительных отклонениях от идеальности это условие не выполняется – начинает устанавливаться ближний порядок среди атомов одинаковых сортов. Законы равнораспределения перестают выполняться, и в таких растворах начинают устанавливаться предпочтительно парные связи однородных атомов А-А и В-В соответственно, что, собственно, и есть эффект расслоения. Предпочтительность связей однородных атомов характеризуется параметром ближнего порядка σ.
Более точная теория расслоения сплавов должна учитывать, кроме ближнего порядка, так же вклад упругой энергии в теплоту смешения. Роль упругой энергии особенно велика в случае больших различий в радиусах атомов компонентов сплава. Если доля термодинамической теплоты смешения, определяемой химическим
168

взаимодействием атомов, мала, то условия расслоения определяются исключительно энергией искажения. Кроме того, в связи с тем, что граница между возникающими при расслоении участками изоморфных твердых растворов должна быть когерентна, то с ее появлением связана упругая деформация сопряжения границ фаз с разным периодом решетки, вызванным различием в концентрациях.
4.8.2. Спинодальный распад
Как показано выше, в системах с положительным отклонением от идеальности в области высоких температур стабильным состоянием может быть однофазный твердый раствор с неограниченной растворимостью, в то время как в области низких температур равновесию отвечает двухфазное состояние – на взаимную растворимость компонентов начинают накладываться ограничения.
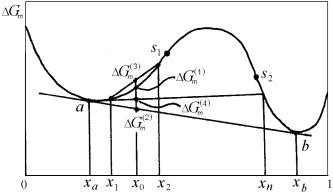
Рассмотрим случай распада в системах с ω-образной непрерывно дифференцируемой концентрационной зависимостью свободной энергии Gm(x). Такая кривая, характерная для случая распада на два изоморфных раствора, была приведена на рис. 4.31. Проведем ее более подробный анализ с помощью рис. 4.32.
Рис. 4.32. Общий вид зависимости свободной
энергии Gm(x) для твердого раствора со спинодальным распадом
Как отмечалось, самопроизвольному распаду при заданной температуре подвержены только сплавы составов от ха до хb, определяемых точками а, b с общей касательной. Но этот распад, опять же в зависимости от состава, может происходить по двум принципиально различным механизмам. Связано это с тем, что ω-образная
169
концентрационная зависимость энергии Гиббса Gm(x) в диапазоне составов от ха до хb имеет две точки перегиба (или спинодальные, поворотные точки) s1, s2 на рис. 4.32. В них выполняется условие равенства нулю второй производной энергии Гиббса раствора по составу:
∂2 Gm (x) |
= 0 . |
(4.196) |
|
∂x2 |
|||
|
|
Поэтому на ω-кривой свободной энергии имеются два типа уча-
стков с прогибом различного характера: |
|
|
|
||
1) |
в середине, между s1 и s2, где |
∂2 |
Gm (x) |
< 0 и кривая обра- |
|
|
∂x2 |
||||
щена выпуклостью вверх; |
|
|
|
|
|
2) |
по краям, между а–s1 и s2–b, где |
∂2 Gm (x) |
> 0 и кривая об- |
||
∂x2 |
|
||||
ращена выпуклостью вниз.
Данный факт отражает разную устойчивость сплавов разных составов к флуктуациям и предопределяет наличие двух механизмов распада соответствующих растворов.
Рассмотрим изотермический распад твердого раствора из области средних составов (состав х0 на рис. 4.32) с начальной свободной энергией Gm(1) .
Конечное равновесное состояние со свободной энергией Gm(2) < Gm(1) не может возникнуть сразу, так как соответствую-
щие равновесные составы ха и хb далеки от х0 – появление макроскопических областей с такими составами маловероятно при малых флуктуациях. Очевидно, что вначале в результате флуктуаций возникнут области с составами, наиболее близкими к х0 (например, х1 и х2). При этом свободная энергия понизится до величины
Gm(3) < Gm(1) , т.е. в рассматриваемом составе сплава любые сколь
угодно малые концентрационные флуктуации будут приводить только к уменьшению свободной энергии системы в целом. Следовательно, для самопроизвольного распада здесь ни на каком этапе не требуется преодолевать энергетические барьеры.
170
Такие процессы не требуют энергии активации. Реально это означает, что для осуществления образования новых фаз – растворов других составов, но с той же кристаллической решеткой – не предъявляются никакие требования к размеру зародышей фаз; здесь нет понятия о критических зародышах. Поэтому такой распад, называемый «спинодальным», происходит сразу во всем объеме исходной фазы; увеличение разности составов и размеров кристаллитов новых фаз во времени за счет диффузионных процессов непрерывно и монотонно понижает свободную энергию всего сплава.
Спинодальный распад при данной температуре идет во всех сплавах, состав которых соответствует области участка кривой свободной энергии, ограниченной точками перегиба (s1 и s2 на рис. 4.32), до тех пор, пока новые фазы не приобретут равновесные концентрации хs1 и хs2. При повышении температуры влияние неидеальности ослабевает (см. разд. 4.8.1), и прогиб на кривой Gm(x) понижается. Спинодальные точки s1 и s2 на изотермических кривых свободной энергии при нагреве постепенно сближаются и, наконец, сливаются в одну критическую точку. Если на диаграмме состояния (рис. 4.33) отмечать составы сплавов, отвечающих спинодальным точкам s1 и s2 при разных температурах, получим кривую RKV, называемую химической спинодалью. Кривая расслоения – линия MKN на рис. 4.33, отвечающая точкам (а, b) с общей касательной на кривой Gm(x), является границей предельной растворимости в твердом состоянии.
Твердые растворы с составами, соответствующими области RKV, будучи переохлаждены до температур ниже спинодали, могут претерпевать спинодальный распад – если позволяют диффузион- но-кинетические ограничения.
Неравновесные твердые растворы в области температур и составов между кривой расслоения MKN и спинодалью RKV, естественно, так же претерпевают распад, но уже не спинодальный. Подробно механизм такого более общего распада обсуждается в следующем разделе.
При температурах выше критической ТK (точка K на рис. 4.33) кривая свободной энергии во всех участках становится обращенной выпуклостью вниз (∂2 Gm/∂х2 > 0). Здесь перегибы на Gm(x) исче-
171

зают, и распад твердых растворов становится невозможен. Но при критической температуре ТK экстремальная точка на кривой Gm(x) при концентрации хK остается спинодальной, т.е. здесь и вторая производная, как и первая, равна нулю. Это позволяет найти критическую точку на кривой спинодали и на кривой расслоения.
Рис. 4.33. Диаграмма (Т–х) с куполом расслоения и спинодалью (а) и кривая свободной энергии (б)
В общем случае имеем:
|
Gm = Hm −TSm = |
Hm −T ( Sid + |
S изб) = |
|
||||||||
= |
Hm −T[ |
S изб − R[(1− x)ln(1− x) + xln x)] = |
(4.197) |
|||||||||
= |
Hm −T |
S изб + RT[(1− x)ln(1− x) + x ln x], |
|
|||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2 G |
m |
= |
∂2 H |
m |
−T |
∂2 S изб |
+ |
RT |
. |
(4.198) |
|
|
∂x2 |
∂x2 |
∂x2 |
x(1 |
− x) |
|||||||
|
|
|
|
|
|
|
|
|||||
В соответствии с условием (4.196), приравнивая (4.198) нулю,
получаем уравнение, определяющее форму спинодали: |
|
|||||||||||
|
|
∂2 |
H |
|
(x) |
|
∂2 S изб(x) |
|
R |
|
|
|
T |
= |
|
|
m |
|
/ |
|
2 |
− |
|
. |
(4.199) |
|
|
|
|
|
||||||||
spin |
|
∂x |
2 |
|
|
∂x |
|
|
|
|
||
|
|
|
|
|
|
|
|
x(1− x) |
|
|||
|
|
|
|
|
|
|
172 |
|
|
|
|
|

Оно имеет два действительных решения относительно х; кривая спинодали в общем случае является асимметричной, так же как и купол расслоения.
Зная аналитический вид концентрационных зависимостей Hm(х) и Sизб(х), можно рассчитать xK из условия (∂Тspin/∂х) = 0, а далее оценить ТK по (4.199). Однако отсутствие надежных экспериментальных данных по концентрационным зависимостям термодинамических свойств для большинства систем вынуждает прибегать к модельным расчетам критических параметров.
Рассмотрим в качестве примера определение ТK для модели регулярного раствора. Для такой системы
HM(х) = х(1 – х)Ω и Sизб(х) = 0.
Тогда из (4.197) имеем:
Gm(х) = х(1 – х)Ω + RT[(1 – x)ln(1 – x) + xlnx].
Выполнив дифференцирование, получим:
∂2Gm (x) |
= − 2Ω + |
RTspin |
= 0 , |
||
∂x2 |
x(1− x) |
||||
что дает для спинодали уравнение симметричной параболы: |
|||||
Тspin = |
2x(1− x)Ω |
. |
(4.200) |
||
|
|||||
|
|
R |
|
||
Дифференцируя (4.200), получаем уравнение для определения значения критической концентрации xKspin для спинодального распада:
= 2Ω(1− 2x) = 0,
T
откуда следует, что xKspin = 0,5. Подставляя это значение в (4.200),
находим значение критической температуры спинодального распада
T spin = |
Ω |
. |
(4.201) |
K 2R
Как видим, координаты критической точки расслоения раствора вообще (см. формулу (4.195)) и по механизму спинодального распада (4.201) совпадают, т.е. спинодаль и кривая расслоения имеют единую критическую точку, что и иллюстрирует рис. 4.33.
173
Симметричность рассмотренной выше «химической» спинодали была получена только формально из-за ограниченности модели регулярных растворов. Расчет кривых расслоения с учетом упругих напряжений, возникающих из-за необходимости согласования (когерентности) периодов решеток на межфазных границах, приводит к их асимметричной форме, неплохо согласующейся с экспериментальными данными. Такие спинодали, лежащие внутри «химической» области, называют «когерентными».
4.8.3. Распад по механизму роста зародышей
Проанализируем, с помощью рис. 4.34, изотермический распад твердого раствора, исходный состав которого х0 лежит в области между спинодалью и кривой расслоения.
Рис. 4.34. Распад по механизму образования и роста зародышей в сплаве состава х0 в системе с непрерывным рядом твердых растворов
Его свободная энергия Gm(1) больше свободной энергии равновесной двухфазной смеси Gm(2) . Если в результате флуктуаций на
ранних стадиях распада образуются две фазы с составами х1 и х2 , близкими к х0, то свободная энергия такой двухфазной смеси будет выше, чем у исходного твердого раствора ( Gm(3) > Gm(1) ) . Это не-
избежное следствие того, что кривая свободной энергии вне спинодального интервала (s1, s2) обращена выпуклостью вниз. Только
174
при возникновении большой разницы по составу свободная энергия начинает понижаться (например, Gm(4) < Gm(1) ).
Таким образом, в отличие от спинодального распада, при котором свободная энергия непрерывно снижается, в рассматриваемом случае фазовое превращение сопровождается вначале повышением, и только затем снижением свободной энергии, т.е. существует термодинамический барьер образования достаточно больших участков новой фазы даже без учета роли поверхностной энергии и энергии упругой деформации решетки. Такой барьер называется «энергией активации». В рассматриваемом случае для того, чтобы активационный распад твердого раствора начался и протекал далее уже с уменьшением свободной энергии, необходимо флуктуационное образование зародышей закритических составов и, соответственно, размеров.
Распад такого типа не имеет особого краткого наименования, так как является обычным активационным, наиболее распространенным в металлических системах. Иногда его называют распадом по механизму образования и роста зародышей, чтобы отличить от спинодального распада. Теоретически он должен протекать в области фигуративных точек между кривой расслоения и химической спинодалью. В реальных системах для спинодального распада требуется переохлаждение ниже когерентной спинодали, и обычный распад протекает и при температурах ниже обычной («химической») спинодали RKV (см. рис. 4.33).
Спинодальный распад может происходить только в системах, в которых тип решетки новых фаз тот же, что и у исходной, да и параметры решеток всех фаз отличаются незначительно. Обычный распад носит более общий характер и может происходить в любых системах, в том числе в системах и с ограниченной растворимостью, и с промежуточными фазами. Выделяющаяся в них новая фаза может отличаться от исходного твердого раствора уже не только составом, но и типом кристаллической решетки. В этом случае свободная энергия системы описывается не гладкой кривой, а двумя кривыми с минимумами и угловой точкой максимума при их пересечении (рис. 4.35).
175
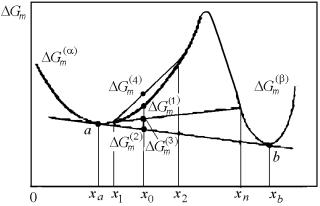
Рис. 4.35. Схема выделения β-фазы из α-раствора по механизму образования и роста зародышей в сплаве состава х0 в системе с ограниченной растворимостью
В целом же термодинамическая схема обычного распада в системе с промежуточной фазой ничем не отличается от такого распада в системе с расслоением одной фазы.
Разность Gm(1) − Gm(2) интегральных молярных энергий раствора является термодинамическим стимулом превращения. Величина
Gоб =V ( Gm(1) − Gm(2) )
представляет уменьшение объемной свободной энергии, вызванное распадом раствора и появлением зародышей новой фазы суммарным объемом V. Но тем самым новообразование приводит к повышению свободной энергии на величину Gупр из-за возникновения упругой деформации матрицы и самой новой фазы. Кроме того, при распаде появляются новые поверхности – границы раздела фаз, что так же
вызывает приращение энергии на величину |
Gпов. В результате для |
изменения энергии всей системы имеем: |
|
G = – Gоб + Gпов + |
Gупр. |
Это выражение иллюстрирует, что образование новых поверхностей и появление упругой деформации препятствует распаду и вносит заметный вклад в величину энергии активации.
176
4.8.4. Термодинамика последовательности выделения фаз
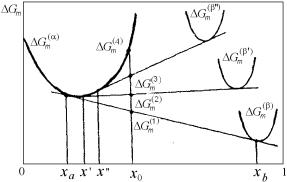
Рассмотрим условия равновесия исходной фазы α с новой стабильной фазой β, отличающейся от исходной как структурой, так и составом. Предположим, что в бинарной системе существуют не только стабильные фазы, но и возможно в определенных условиях образование метастабильных β′- и β′′-фаз, свободная энергия которых больше, чем у устойчивой β-фазы (рис. 4.36). Как видно из приведенного рисунка, в стабильном равновесии с β-фазой находится твердый раствор состава ха, а в метастабильном равновесии с фазами β′ и β′′ находится α-фаза составов х′ и х′′ соответственно.
Следовательно, растворимость в метастабильной фазе в другой фазе всегда выше растворимости стабильной фазы.
В сплаве состава х0 свободная энергия смеси фаз α+β меньше, чем у смесей фаз α+β′ и α+β′′ ( Gm(1) < Gm(2) < Gm(3) ). Следователь-
но, снижение свободной энергии при образовании стабильной фазы больше, чем при образовании метастабильных:
Gm(4) − Gm(1) > Gm(4) − Gm(2) > Gm(4) − Gm(3)
Рис. 4.36. Равновесие α-фазы со стабильной β-фазой и метастабильными β′- и β′′-фазами
Следует учитывать, что этот анализ не учитывает вкладов поверхностной и упругой энергий в общем изменении свободной энергии типа (4.90), т.к. на рис. 4.36 представлены концентрацион-
177
ные зависимости объемной свободной энергии. Значения поверхностной энергии на границах α-фазы с фазами β, β′ и β′′ могут очень сильно различаться. Если кристаллическая решетка стабильной β-фазы резко отличается от решетки исходной α-фазы, когерентная граница не может возникнуть. В то же время структура метастабильных фаз β′ и β′′ ближе к структуре исходной α-фазы, и межфазные границы α/β′ и α/β′′ могут быть когерентными или полукогерентными. Поверхностная энергия на таких границах намного ниже, чем на некогерентной границе α/β. Если при этом выигрыш в поверхностной энергии существенно перекрывает проигрыш в объемной свободной энергии, то в соответствии с выражением (4.90) работа образования критического зародыша Gкр метастабильной фазы будет ниже, чем у стабильной, и скорость зарождения метастабильной фазы будет выше. В случае когерентных или полукогерентных границ метастабильных фаз для уменьшения Gкр выигрыш в поверхностной энергии должен так же перекрывать возрастание упругой энергии, связанной с такими границами.
Если в системе существуют различные метастабильные фазы, то при данной степени переохлаждения с увеличением времени выдержки вначале из-за большой скорости зарождения будет образовываться метастабильная фаза, у которой работа образования критического зародыша минимальна. Затем появляются метастабильные фазы с большей энергией образования критического зародыша и в последнюю очередь – стабильная фаза с самой высокой энергией активации образования и низкой скоростью зарождения.
Таким образом, последовательность образования фаз регулируется не достигаемым уровнем объемной свободной энергии, а величиной энергетического барьера при зарождении новой фазы, которая сильно зависит от поверхностной энергии на межфазной границе. Чем больше указанный барьер, тем позднее образуется соответствующая фаза. Эта закономерность называется «правилом ступеней».
Когда после образования β′′-фазы появляется более устойчивая β′-фаза, то около ее кристаллов в исходной α-фазе устанавливается равновесная концентрация х′, в то время как на границе с β′′-фазой
178
ранее установилась концентрация α-раствора х′′. Диффузионное выравнивание состава в α-растворе будет приводить к уменьшению его концентрации вблизи границы α⁄β′′, и β′′-фаза должна растворяться в ненасыщенном по отношению к ней слое α-раствора. Одновременное увеличение концентрации α-раствора на границе α⁄β′ будет стимулировать рост β′-фазы из пересыщенного по отношению к ней слоя α-раствора. Следовательно, более стабильная β′- фаза растет за счет растворения менее стабильной β′′-фазы путем диффузионного переноса второго компонента через матричный α- раствор.
Аналогично, при появлении стабильной фазы β должна растворяться фаза β′. Это соответствует общей закономерности: образо-
вание более стабильной фазы приводит к растворению ранее образовавшейся менее стабильной фазы, которую в этом смысле можно считать промежуточной.
Одним из видов промежуточных метастабильных фаз являются зоны Гинье–Престона (ГП), которые с термодинамической точки зрения рассматриваются как самостоятельные метастабильные фазы, имеющие характер когерентных «предвыделений» с той же решеткой, что и матрица. Рассмотрим гипотетическую систему, в которой в α-растворе могут образовываться зоны ГП, промежуточная β′-фаза и стабильная β-фаза (рис. 4.37).
Рис. 4.37. Зависимость свободной энергии расслаивающегося с образованием зон ГП
пересыщенного α–раствора, метастабильной β′- и стабильной β-фазой
179

Приведенная на этом рисунке кривая Gm(α) представляет зависи-
мость свободной энергии раствора от состава α-фазы, которая может изоморфно расслаиваться с образованием зон ГП (по аналогии с рис. 4.33). Применение методов геометрической термодинамики дает некоторый состав матрицы xα−ΓΠ, находящийся в метастабильном равновесии с зонами ГП. Промежуточная β′-фаза и стабильная β-фаза имеют кристаллическую решетку, отличную от решетки мат-
рицы, и поэтому кривые свободной энергии Gm(β) и Gm(β') не являются продолжением кривой Gm(α) , как для фазы зон ГП. Состав матрицы
хα−β′ , находящейся в метастабильном равновесии с промежуточной β′-фазой, и хα−β, находящейся в равновесии со стабильной β-фазой, определяется аналогично – проведением касательных. Таким образом, так же как и ранее, можно сделать вывод, что концентрация второго компонента в растворе, равновесным с зонами ГП, будет всегда выше, чем в растворе, находящимся в равновесии с β′-фазой, и тем более чем с раствором, равновесным с β-фазой.
Рис. 4.38. Диаграмма (Т–х) с линиями растворимости стабильной β-фазы, метастабильной β′-фазы и зон ГП
В общем случае на диаграмме состояния кривая растворимости представлена на рис. 4.38 в виде линии растворимости (сольвуса) стабильной фазы. В соответствии с проведенным выше анализом линии существования метастабильной β′-фазы и зон ГП должны находиться ниже кривой растворимости β-фазы, что согласно по-
180
строениям на рис. 4.37 должно приводить к изменению термодинамических параметров растворения метастабильных фаз.
Выше постулировалось, что последовательность образования фаз регулируется величиной энергетического барьера при зарождении новой фазы. У зон ГП поверхностная энергия минимальна, а у некогерентных выделений стабильной фазы – максимальна. Поэтому для значений энергий образования критических зародышей
Gкр наблюдается последовательность: GкрГП Gкр' Gкр . При
старении сплава с выделением зон ГП энергетический барьер зарождения выделений создается не только из-за образования поверхности раздела, но и из-за упругой деформации решетки за счет конечности объема этой фазы, и приведенное неравенство выполняется только в том случае, если выигрыш в поверхностной энергии перекрывает возможный проигрыш в энергии упругой деформации.
4.8.5.Kоагуляция выделений
Впроцессе старения – непрерывного распада твердого раствора
–суммарный объем выделений увеличивается, а концентрация легирующего элемента в материнском растворе снижается. Когда его состав приближается к равновесному, суммарный объем выделений почти перестает изменяться. Но микроструктура такого только что состаренного сплава является еще нестабильной, так как образовавшиеся дисперсные выделения склонны к укрупнению (коагуляции).
Движущей силой коагуляции является разность свободных энергий мелких и крупных частиц. В состаренном сплаве из-за разных локальных условий роста размеры выделений разные. Чем меньше выделение, тем больше доля атомов, расположенных на его поверхности, и тем, следовательно, выше средняя свободная энергия, приходящаяся на 1 г-атом выделения.
На рис. 4.39 показано, что кривая свободной энергии мелких
частиц -фазы Gm( )мелк расположена выше кривой свободной энергии крупных частиц этой же фазы Gm( )круп . Из приведенного рисун-
181
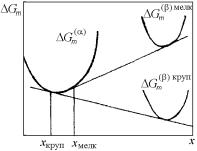
ка следует, что концентрация xмелк(α) α-раствора, находящегося в равновесии с мелкими выделениями β-фазы, должна быть выше, чем при равновесии с крупными выделениями xкруп(α) . Это подтвер-
ждается анализом размерного эффекта растворимости Гиббса– Томсона.
Рис. 4.39. Концентрационные зависимости свободной энергии
α-твердого раствора |
G(α) , |
||
|
|
|
m |
а также крупных |
G(β)круп |
||
|
|
|
m |
и мелких |
G(β)мелк |
выделений |
|
|
m |
|
|
β-фазы
Проведенный выше анализ изменения пределов растворимости строго применим только для плоских поверхностей раздела фаз. Для искривленных поверхностей, например, сферических с радиусом R, появлятся необходимость в учете дополнительных энергетических членов. Рассмотрим систему, в которой сферические частицы β-фазы радиусом R, площадью поверхности Sβ и удельной поверхностной свободной энергией σ находятся в равновесии с матрицей α-фазы.
В процессе фазового превращения, при котором dn атомов переходят из α-фазы в β-фазу, возникает дополнительная энергия σdSβ, обусловленная увеличением площади поверхности β-частиц. При этом химический потенциал β-фазы увеличивается на величину σ(dSβ/dn) и условия равновесия по второму компоненту имеют вид
μ(2α(R) ) = μ(2β()R) = μ(2β∞) + σ(dSβ / dn) , |
(4.202) |
где индексы R и ∞ означают сферическую или плоскую поверхность. В приближении сферических частиц, используя мольный объем Vβ на г-атом β-фазы, можно получить:
dS β |
= |
2V |
β |
|
|
|
|
|
. |
(4.203) |
|
dn |
R |
|
|||
|
|
|
|
||
|
182 |
|
|
|
|

Учитывая, что условия равновесия фаз с плоскими границами имеют вид μ(2α(∞) ) = μ(2β()∞) , из (4.202) и (4.203) получаем:
μ(2α(R) ) −μ(2α(∞) ) = 2σRV β .
Заменяя химический потенциал на их выражения через активности и используя для растворенного вещества закон Генри, получаем:
ln |
x2(α(R) ) |
= |
2σV β |
. |
|
x2((α∞) ) |
kTR |
||||
|
|
|
Полученное соотношение известно как уравнение Гиббса– Томсона, Томсона–Гельмгольца или Томсона–Фрейндлиха. Оно показывает, что растворимость второго компонента в α-фазе экспоненциально зависит от радиуса кривизны поверхности включения β-фазы. При этом, чем меньше радиус частицы, тем больше около нее равновесная концентрация раствора.
Таким образом, в материнском растворе существует градиент концентраций второго элемента между зонами около выделений разного размера. Этот градиент и вызывает коагуляцию, являясь движущей силой диффузии, выравнивающей концентрацию. Концентрация раствора на границе с мелким выделением понижается, и это выделение растворяется, пытаясь поддержать равновесную концентрацию на своей границе. Тот же диффузионный процесс повышает концентрацию на его границе с крупным выделением. Раствор здесь пересыщается, и второй компонент переходит в β-
фазу, поддерживая равновесную концентрацию xкруп(α) . Крупные
частицы β-фазы, таким образом, растут при одновременном растворении мелких выделений. Следовательно, коагуляция выделений во время распада происходит вследствие переноса вещества через матричный раствор при растворении более мелких и росте более крупных выделений.
Коагулировать могут не только выделения стабильной фазы, но и выделения зон ГП и промежуточных фаз, так как концентрация раствора, находящегося в метастабильном равновесии с ними, так же зависит от размера выделений. Поэтому коагуляцию можно на-
183
блюдать и на разных промежуточных стадиях распада твердых растворов.
4.8.6. Термодинамика мартенситных превращений
В твердом состоянии возможны превращения, не имеющие аналогов среди рассмотренных выше типов фазовых превращений. К таким превращениям, прежде всего, относятся мартенситные превращения, являющиеся по своей кинетике бездиффузионными и приводящие к изменению типа кристаллической структуры без перераспределения компонентов между новыми фазами. К этому типу превращений относится большинство полиморфных превращений в металлах и сплавах.
Название превращения связано с именем немецкого металловеда А. Мартенса. Мартенситное превращение определяется как реакция, продукт которой получается из материнской фазы путем координированного коллективного сдвига большого количества атомов на расстояния порядка межатомных, но без изменения состава и без обмена атомов местами. Следствием и одновременно условием этого кооперативного движения атомов является совпадение (или «когерентность») решеток исходной и растущей фаз на фронте превращения, на их границе раздела. В связи с этим основной проблемой при изучении этого типа превращений является развитие кристаллографической теории, рассмотрение которой выходит за рамки настоящего пособия. На долю термодинамического рассмотрения проблем мартенситных превращений остается главным образом изучение термодинамических стимулов и термодинамической возможности бездиффузионных превращений.
Большинство мартенситных превращений, происходящих в металлах и сплавах, являются фазовыми переходами первого рода. Мартенситное превращение не может начинаться при любом сколь угодно малом переохлаждении относительно равновесной температуры Т0. Результирующее изменение свободной энергии в точке начала мартенситного превращения Тм, так же как и для других типов фазовых превращений, может быть представлено выражением типа (4.90):
184
G = – Gоб + Gпов + Gупр.
Действительно, образование кристалла мартенсита связано не только с существованием отрицательного вклада объемной свободной энергии Gоб, являющегося термодинамическим стимулом превращения, но и с появлением положительных энергетических вкладов от новых поверхностей, и в особенности, от деформаций, препятствующих превращению. Энергия упругой деформации возникает из-за изменения объема при фазовом превращении, а так же из-за несовпадения решеток мартенсита и исходной фазы.
Изменение свободной энергии G происходит при образовании центра новой фазы, содержащего n атомов. В рамках термодинамики необратимых процессов можно показать, что роль движущей силы процесса роста зародыша мартенситной фазы играет величина d G(п)/dn. А вот вопрос о том, что представляют собой зародыши мартенсита – до сих пор дискуссионный в проблеме мартенситных превращений. По-видимому, вероятность гомогенного зарождения, связанного с флуктуационным образованием зародыша критического размера, мала из-за высокой энергии упругих искажений и, следовательно, большой работы образования зародыша. Большинство гипотез предполагает гетерогенное зарождение мартенсита, связанное с наличием и особенностями взаимодействия структурных дефектов. Тем не менее, приближенные энергетические оценки критических размеров образования зародыша могут быть выполнены в рамках теории гомогенного зарождения, приведенной в п. 4.8.3.
Исходя из того, что конечные равновесные зерна мартенсита имеют форму чечевиц (линз), опишем зародыш мартенсита как сплющенный сфероид объемом (4π/3)r2c и с площадью поверхности 2πr2, где r – радиус, с – половина толщины сфероида. Тогда выражение типа (4.90) для изменения свободной энергии при образовании зародыша имеет вид:
G = |
4 |
πr 2c |
Gоб + |
4 |
πr 2c(Ac / r) + 2πr 2σ , |
(4.204) |
|
3 |
3 |
||||||
|
|
|
|
|
где Ас/r – энергия упругой деформации на единицу объема зародыша. Критические параметры зародыша, определяемые условиями: ∂( G) ⁄∂r = 0 и ∂( G) ⁄∂с = 0, из (4.204) оцениваются в виде:
185
r |
= |
|
4Aσ |
|
|
; |
c |
= − |
|
|
2σ |
; |
||
( |
G |
|
) |
|
|
G |
||||||||
кр |
|
|
|
|
кр |
|
|
|
|
|||||
|
|
|
|
об |
|
|
|
|
|
|
об |
|
||
|
|
|
|
32 |
|
|
A2σ3 |
|
|
|
|
|
||
( |
Gкр) = |
|
π |
|
|
. |
|
|
||||||
3 |
|
( |
Gоб) |
4 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Для начала мартенситного превращения необходимо так переохладить систему ниже температуры Т0 , чтобы термодинамический стимул превращения Gоб достиг необходимой величины. Поэтому температура начала мартенситного превращения всегда находится ниже температуры Т0, однако точное термодинамическое определение температуры Тм невозможно. Как отмечалось в п. 4.8.3, работа образования критического зародыша зависит от степени переохлаждения Т = Т0 – Тм. Кроме того, специфические особенности мартенситных превращений, в частности, их сдвиговый характер, накладывают свои условия на сложный вид функциональных зависимостей термодинамических стимулов от деформационных параметров в процессе превращения.
На рис. 4.40 приведена зависимость величины термодинамической движущей силы, или стимула превращения, Gоб от угла сдвиговой деформации θ, непрерывно увеличивающегося в процессе превращения элементарной кристаллической ячейки исходной фазы в мартенситную.
Приведенные результаты получены в рамках термодинамической теории сдвига. В исходном состоянии, когда θ = 0, кривизна Gт определяется знаком производных модуля сдвига μ, определяемого как ∂2 Gт/∂θ2. При некотором критическом значении θкр величина активационного барьера, отделяющего исходное состояние от мартенситного, является максимальной и равна G = Gоб + Gкр. Величина Gкр соответствует добавочным членам, характеризующим упругую деформацию, в выражении (4.90). После преодоления активационного барьера G → 0 при θ → θм, и свободная энергия
самопроизвольно уменьшается до значения Gm(M ) при окончании сдвигового превращения (рис. 4.40,а). С ростом температуры (уменьшением степени переохлаждения Т) Gкр увеличивается, но активационный барьер уменьшается из-за превалирующего влияния
186

Gоб. Наклон кривой свободной энергии в окрестностях θ = 0 при этом слегка уменьшается, ибо модуль сдвига μ уменьшается с температурой (рис. 4.40,б).
Рис. 4.40. Зависимость объемной свободной энергии от угла сдвига при мартенситном превращении (а) и нормализованные к θ = 0 зависимости свободной энергии от угла сдвига для различных температур (Т1<T2) (б)
Мартенситная реакция может быть индуцирована при температурах и выше Тм с помощью приложения внешних сдвиговых напряжений; они нейтрализуют внутренние напряжения, возникающие в процессе превращения. Однако существует некоторая температура Т′ (Тм < Т′ < Т0), выше которой превращение не может быть индуцировано никакими внешними напряжениями.
Проведем анализ термодинамической возможности мартенситного превращения бездиффузионного типа для простейшего случая системы, характеризующейся полиморфизмом чистого компонента А и α-раствора на его основе (рис. 4.41,а). При достаточно медленном охлаждении сплава концентрации х0 в интервале температур от точки 1 до точки 2 протекает полиморфное превращение β → α.
При любой температуре, как было показано ранее, α- и β- твердые растворы характеризуются своими концентрационными зависимостями свободной энергии, приведенными на рис. 4.41,б для температур Т1 < T2 < T3. При высокой температуре Т ≥ Т3 стабильное состояние сплава состава х0 есть β-фаза. При температурах Т1 и Т2 стабильное состояние есть смесь α- и β-фаз с составами, соответствующими точкам на общей касательной. Ниже температуры Тα стабильной фазой является α-фаза.
187
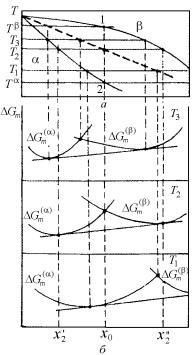
Стабильное равновесие фаз, составы которых определяются общей касательной к кривым свободной энергии, достигается при очень медленном охлаждении. Тогда полиморфное превращение сопровождается равновесным диффузионным перераспределением компонентов между исходной и новой фазами. При ускоренном охлаждении сплава из β-области такое перераспределение компонентов может быть полностью подавлено.
Сопоставим значения свободной энергии α- и β-фаз одинакового состава х0 при различных температурах. Так, имеем: при
|
температуре Т1 – |
Gmβ |
> |
Gmα ; |
Рис. 4.41. Участок (Т, х) диаграммы |
при температуре Т2 : |
Gmβ = |
Gmα ; |
|
с полиморфизмом твердого раствора |
при Т3 : Gβ < < Gα . |
Следова- |
||
(а) и кривые свободной энергии α- и |
m |
m |
|
|
β-фаз при температурах Т1, Т2, Т3 (б) |
тельно, свободная энергия исход- |
|||
|
ной β-фазы при охлаждении воз- |
|||
растает интенсивнее, чем свободная энергия α-фазы того же состава. По-видимому, кривые температурной зависимости свободной энергии двух модификаций твердого раствора одинакового состава идут, пересекаясь, аналогично соответствующим кривым двух модификаций чистого компонента. Принципиальное различие состоит в том, что в случае чистого металла точка пересечения кривых свободных энергий Т0 отвечает температуре стабильного равновесия двух его полиморфных модификаций, а в случае сплава – температуре метастабильного равновесия переохлажденного β-раствора с метастабильным α-раствором того же состава. Если бы диффузионное перераспределение компонентов успело пройти, то при рас-
188
сматриваемой температуре метастабильного равновесия Т2 в сплаве состава х0 образовалась бы равновесная смесь фаз αх′ + βх′′ разного состава.
Указанным способом для любого сплава рассматриваемой системы можно отметить на диаграмме состояния температуры равенства свободных энергий метастабильных α- и β-фаз одинакового состава. Геометрическим местом точек таких температур является пунктирная линия на рис. 4.41,а.
В любом сплаве, при охлаждении исходной β-фазы до температуры ниже этой линии, ее свободная энергия становится больше, чем у α-фазы того же состава. Следовательно, появляется термоди-
намический стимул G = Gmα – Gmβ полиморфного превращения
β → α без изменения состава. В твердом состоянии, из-за малой диффузионной подвижности атомов, переохлаждения ниже указанной линии реализуются достаточно легко, и полностью бездиффузионное полиморфное превращение твердого раствора становится возможным термодинамически. Кинетически такое превращение возможно, так как оно совершается путем мартенситного механизма.
4.9. Системы с отрицательным отклонением от идеальности
В данном разделе рассматриваются системы с отрицательным отклонением от идеальности (Ω < 0) – случай, когда εАВ меньше по абсолютной величине, чем 1/2(εАА+εВВ). Этот вариант встречается в системах, где законы взаимодействия разнородных атомов металлов существенно отличаются от законов взаимодействия атомов одного сорта. В растворах, в которых параметр взаимодействия Ω разнородных компонентов отрицателен, а по модулю или сравним с тепловой энергией (|Ω| ≈ RT), или больше нее (|Ω| > RT), наблюдается образование преимущественных связей типа А–В. При этом распределение атомов по узлам решетки отклоняется от среднестатистического; в таких системах реализуются структуры с упорядоченным расположением атомов в кристаллической решетке. В сплавах с еще большими (|Ω| >> RT) отрицательными энергиями
189
взаимодействия компонентов возникают химические соединения – промежуточные фазы по терминологии металловедения.
4.9.1.Упорядочение
Всплавах с отрицательным отклонением от идеальности часто реализуется упорядоченное распределение атомов каждого сорта по узлам определенного типа в кристаллической решетке. Такие сплавы называются упорядоченными. Упорядоченный сплав обладает трансляционной симметрией: распределение атомов определенного сорта повторяется во всех элементарных ячейках кристалла, т.е. упорядоченное состояние обладает дальним порядком по расположению атомов любого сорта.
При повышении температуры, когда неидеальность системы уменьшается, наблюдается переход части атомов со «своих» узлов на «чужие». Дальний порядок постепенно исчезает, и сплав плавно становится неупорядоченным, что трактуется как фазовый переход
порядок↔беспорядок. В некоторых случаях еще до достижения температуры плавления концентрации атомов на узлах различных типов становятся равновероятными. Критическая температура ТK, при которой совершается такой переход, называется температурой фазового перехода порядок↔беспорядок или температурой упорядочения.
В не полностью упорядоченном сплаве свойством симметрии обладают не реальные атомы, а только их вероятности замещения узлов разного типа. При этом имеются случаи, когда вероятности замещения узлов при переходе изменяются скачком, и упорядочение происходит как фазовый переход I рода. Однако чаще эти вероятности изменяются непрерывно, и тогда переход порядок↔беспорядок является переходом II рода.
Рассмотрим бинарный сплав замещения, состоящий из N атомов, занимающих N узлов, и содержащий NA атомов А и NB атомов В. Разделим кристаллическую решетку на две подрешетки, образованные соответственно из N(1) узлов первого типа, предназначенных в упорядоченном сплаве для атомов А, и N(2) узлов второго типа, предназначенных для атомов В. Количество узлов N(1), N(2) со-
190
относятся как небольшие целые числа. Например, для ОЦК метал-
лов это будет 1:1, 1:3; для ГЦК – 1:1, 1:3, 3:5; ГПУ – 1:1, 1:3. Если реальные количества веществ удовлетворяют таким соотношениям, то сплав называется стехиометрическим. В стехиометрических сплавах выполняется условие: NA = N(1) ; NB = N(2). Составы таких сплавов записываются как химические формулы, например AuCu
или Сu3Au.
Введем обозначения для относительных концентраций (мольных долей) реальных атомов:
хА = NA /N и хВ = NВ /N ,
и для относительных концентраций узлов первого и второго типа
ν = N(1)/N и 1 – ν = N(2)/N.
Заметим, что для сплавов стехиометрического состава:
хА = ν и хВ = 1 – ν.
В полностью упорядоченном сплаве все атомы А находятся в узлах N(1), и все атомы В – в узлах N(2); в неупорядоченном сплаве
атомы занимают любые позиции. Обозначим через N A(1) , N A( 2 ) , NB(1) , NB(2) реальное число атомов А и В, находящееся на узлах первого и второго сорта в неупорядоченном сплаве. Тогда имеем:
N |
(1) |
+ N |
(2) |
= N ; |
|
(1) |
|
(2) |
|
|
|
|
A |
|
A |
A |
NB |
+ NB |
= NB ; |
(4.205) |
|||
N |
(1) |
+ N |
(1) |
= N (1) ; |
|
(2) |
|
(2) |
|
|
|
N |
+ N |
= N |
(2) |
|
|||||||
|
A |
|
B |
|
A |
B |
. |
|
|||
|
|
|
|
|
|
|
|
|
|
||
Введем вероятности Р замещения атомами А и В узлов первого и второго типа, определяемые формулами:
P(1) = N |
(1) / N (1) |
; |
P(1) = N |
(1) / N (1) |
; |
||||||
|
A |
|
A |
|
|
|
B |
|
B |
|
|
P( |
2) |
= N (2) |
/ N (2) |
; |
P( |
2) |
= N (2) |
/N (2) . |
(4.206) |
||
A |
|
A |
|
|
|
B |
|
B |
|
|
|
Введенные в выражениях вида (4.206) вероятности эквивалентны величинам, обозначающим долю мест, занимаемых «своими» или «чужими» атомами. Эти вероятности являются априорными вероятностями; они определяются для каждого узла независимо от того, какими атомами заняты другие узлы. В неупорядоченных сплавах PA(1) = PA(2) = хА, PB(1) = PB(2) = хВ. Здесь все узлы решетки ха-
рактеризуются одинаковыми парами вероятностей хА и хВ замещения их атомами А или В и являются однотипными.
191
В упорядоченных сплавах узлы решетки разделяются на подрешетки двух типов, обладающие разными вероятностями замещения их атомами А или В. Из (4.205) и (4.206) следует, что вероятности удовлетворяют следующим соотношениям:
P(1) |
+ P(1) |
= 1; P( |
2) |
+ |
P(2) |
= 1 ; |
|
|
A |
B |
A |
|
|
|
B |
|
|
|
ν P(1) |
+ (1–ν) P( |
2) |
= хА. |
(4.207) |
|||
|
A |
|
|
A |
|
|
|
|
Введем параметр α, характеризующий упорядочение в сплаве и называемый степенью дальнего порядка, которую определим как
|
P(1) |
− x |
A |
|
|
α = |
А |
|
. |
(4.208) |
|
1−ν |
|
||||
|
|
|
|
||
Для сплавов стехиометрического состава из (4.207) с использованием (4.206) можно получить:
|
P(1) |
− x |
A |
|
P(1) |
|
α = |
А |
|
=1− |
B |
(4.208а) |
|
1− xA |
|
xB |
||||
|
|
|
|
|||
или в эквивалентной форме через второй компонент:
|
P(2) |
− x |
|
|
P(2) |
|
|
α = |
B |
|
B |
=1− |
A |
. |
(4.208б) |
1− xB |
|
|
|||||
|
|
|
xA |
|
|||
Из (4.208) вероятности могут быть выражены через α и концентрации атомов:
P(1) |
= x |
A |
+ αx |
B |
; |
P(1) |
= x |
B |
(1−α); |
|
A |
|
|
|
B |
|
|
(4.209) |
|||
(2) |
|
|
|
|
|
(2) |
|
|
|
|
= xA (1−α); |
|
|
|
|
||||||
PA |
PB |
= xB + αxA . |
|
|||||||
Из определения степени дальнего порядка α видно, что она связана с вероятностью замещения, а в соответствии с (4.206) и с числом атомов разного сорта, занимающих узлы различного типа. Таким образом, α действительно характеризует дальний порядок в сплаве. Как видно из (4.208), (4.208а) и (4.208б), для полностью разупорядоченных сплавов, где
P(1) |
= x |
B |
; |
P(1) |
= x |
A |
; |
B |
|
|
A |
|
|
||
PB( 2 ) = x B ; |
PA( 2 ) = x A , |
||||||
степень дальнего порядка α обращается в нуль, а для полностью упорядоченного сплава стехиометрического состава, где PA(2) = 0 и
192
PB(1) = 0, αmax = 1. Из формул (4.208а) и (4.208б) можно показать, что при различных соотношениях Pi(1,2) и хi степень дальнего по-
рядка α как функция состава для сплавов с ν = 1/2 и ν = 1/4 имеет вид, представленный на рис. 4.42.
Экспериментальные и теоретические исследования показали, что степень дальнего порядка не полностью определяет характер взаимного расположения атомов разного сорта по узлам кристаллической решетки. Различия по энергиям взаимодействия между атомами разного сорта может оказаться достаточным для того, чтобы вблизи каждого из атомов оказались преимущественно соседи друго-
го сорта, даже если в целом в твердом растворе не существует дальнего порядка. Такое распределение атомов называется ближним порядком. В простейших случаях ближний порядок распространяется на одну или две координационные сферы; хотя иногда корреляция ощущается и на более далеких расстояниях.
В соответствии с классической теорией ближнего порядка, впервые разработанной Бете, степень ближнего порядка σ определяется через количество разноименных пар атомов NAB в сплаве следующим образом:
σ = |
N AB −(N AB )min |
, |
(4.210) |
(N AB )max −(N AB )min |
где индексы max и min относятся к обозначению количества пар А– В в полностью упорядоченном и неупорядоченном сплавах соответственно. В такой форме представления изменение степени ближнего порядка лежит в пределах 0 ≤ σ ≤ 1.
Существуют и другие выражения для параметра ближнего порядка. Так, мерой ближнего порядка по Каули является отношение числа пар разноименных атомов для i-ой координационной сферы (или числа разноименных связей) (NAB)i к (NAB)min. В связи с этим
193
степень ближнего порядка для i-ой координационной сферы определяется формулой:
σ*i =1− |
(N AB )i |
. |
(4.211) |
|
|||
|
(N AB )min |
|
|
Из такого определения параметра ближнего порядка следует, что σi* < 0, если ближайшими соседями являются разноименные атомы, σi* > 0, если ближайшие соседи – атомы одного сорта.
Из простых статистических соображений (NAB)max равно общему числу связей в кристалле в предположении, что все связи разноименные. Для полностью разупорядоченного кристалла (NAB)min равно вероятности того, что атомы А и В являются ближайшими соседями, когда хАхВ + хВхА = 2хАхВ, умноженному на общее число связей
в кристалле. Следовательно: |
|
(NAB)max = z.N/2, |
|
(NAB)min = 2 хА хВz.N/2 = хА хВz.N, |
(4.212) |
где z – координационное число.
В этом случае можно, например, из (4.210) вычислить число раз-
ноименных пар в сплаве с ближним порядком σ: |
|
NAB = zN[σ/2 + хА хВ(1 – σ)]. |
(4.213) |
В общем случае ближний порядок должен характеризоваться параметрами корреляции для разных координационных сфер, учитывающими зависимость вероятности замещения атомами А и В узлов данного типа от размещения атомов на других узлах (в отличие от априорных вероятностей). Только учет корреляции позволяет объяснить, что степень ближнего порядка σ (в отличие от степени дальнего порядка α) не обращается в нуль в точке фазового перехода при ТK.
4.9.2. Термодинамическая теория упорядочения
Переход неупорядоченного сплава в состояние с дальним порядком, совершающийся при температуре ТK, может быть как фазовым переходом первого, так и второго рода. В случае перехода первого рода (например, в сплавах Сu3Au) степень дальнего порядка α изменяется скачком от нуля до некоторого конечного значе-
194
ния. При этом скачкообразно изменяются свойства сплава, которые выражаются через первые производные свободной энергии по р и Т (соответственно это объем V и энтропия S). Проявляется это в наличии теплоты перехода. При переходе второго рода (например, β- латуни) степень дальнего порядка α меняется непрерывно, увеличиваясь от нуля до максимального значения при понижении температуры. Объем и энтропия при этом так же изменяется непрерывно. Теплота перехода отсутствует. При ТK скачкообразные изменения испытывают вторые производные от энергии Гиббса, а именно теплоемкость, сжимаемость, коэффициент теплового расширения. Конечно, скачком меняется и симметрия кристаллической решетки, так как исчезают какие-либо элементы симметрии в распределении вероятностей замещения узлов атомами разных сортов.
Термодинамическая теория упорядочения базируется на учете свойств симметрии кристалла и на применении общих термодинамических соотношений; какие-либо конкретные атомные модели сплава не используются.
Предположим, что в бинарном упорядочивающемся сплаве – растворе замещения – переход порядок–беспорядок является фазовым переходом второго рода. В этом случае при температуре T, немного меньшей TK , в неупорядоченной фазе степень дальнего порядка мала и может рассматриваться как малый параметр. Поэтому разложим свободную энергию Гиббса сплава Gm(T, p, xA, α) в ряд по степеням α. При этом будем предполагать, что α может принимать не только равновесные значения, однозначно определяемые из условия минимума Gm при заданных T, p, xA, но и произвольные неравновесные значения. Учитывая в разложении члены до четвертого порядка включительно, имеем:
Gm(T, p, xA, α) = G0 + A1α + ½(A2α2) + ⅓(A3α3) + ¼(A4α4), (4.214)
где коэффициенты разложения являются функциями T, p, xA .
Для сплавов с фазовым переходом второго рода замена α на –α соответствует переименованию узлов первого и второго типа (исходя из соображений симметрии кристаллической решетки, например, β-латуни), не приводя к изменению свободной энергии. Следовательно, в разложении (4.214) члены с нечетными степенями α
195

должны отсутствовать, а А1 и А3 тождественно обращаться в нуль. Тогда
Gm(T, p, xA, α) = G0 + 1/2(A2α2) + 1/4(A4α4). (4.215)
Равновесное значение степени дальнего порядка в сплаве при
данных T, p и xA определяется из условий минимума |
Gm: |
|
∂( |
Gm)/∂α = α(А2 + А4α2) = 0, |
(4.216) |
∂2( |
Gm)/∂α2 = А2 + 3А4α2 > 0. |
(4.217) |
Уравнение (4.216) имеет решение α = 0, соответствующее не-
упорядоченному состоянию сплава, и решение |
|
α2 = –А2/А4, |
(4.218) |
отвечающее упорядоченному состоянию. Таким образом, в неупорядоченном состоянии минимум Gm соответствует α = 0 и А2 > 0. Подставляя (4.218) в (4.217) находим, что в упорядоченном состоянии А2 < 0, а минимуму Gm соответствует не равное нулю значе-
ние α (рис. 4.43).
Следовательно, при переходе через точку упорядочения А2 меняет знак, а в самой этой точке А2(T, p, xA) = 0, что является уравнением поверхности точек перехода порядок–беспорядок в пространстве T, p, x.
В самой точке перехода α = 0,
А2 = 0 и ∂2( Gm)/∂α2 = 0. Поэтому для того, чтобы эта точка соответствовала устойчивому состоянию ( Gm имела минимум), необхо-
димо, чтобы в ней выполнялось условие А4 > 0. Это условие должно выполняться так же и в окрестности TK.
Выясним теперь, как зависит равновесное значение α от T в упорядоченной фазе вблизи TK. Предположим, что при заданных p и xA функцию А2(Т) можно разложить в ряд по степеням T–TK и при малых значениях T–TK ограничиться линейным членом разложения:
А2 = а(T – TK). (4.219)
При этом постоянный коэффициент а > 0, так как для неупорядоченной фазы, при T > TK , А2 > 0.
196

Подставляя (4.219) в (4.218) и ограничиваясь нулевым членом А40
разложения А4 по T–TK , получаем: |
|
α2 = а(T – TK )/ А0 . |
(4.220) |
4 |
|
Таким образом, в упорядоченных сплавах, в которых переход порядок–беспорядок является фазовым переходом второго рода,
при заданных p и xA вблизи TK имеем: α ≈ TК −T . Подставляя
(4.220) в (4.215) и учитывая (4.219), получим для равновесных состояний упорядоченного сплава
Gm(T, p, xA)= Gо – а.2 (T – TK )2 / (4А40 ) (при Т ≤ ТK) , (4.221)
где G0(T, p, xA) – свободная энергия неупорядоченного сплава. Из (4.221) можно получить выражения для производных сво-
бодной энергии по температуре для упорядоченного состояния:
∂( Gm)/∂T = ∂ G0/∂T + а.2 (TK – T) / (2А0 ) , |
(4.222) |
4 |
|
∂2( Gm)/∂T2 = ∂2 G0/∂T2 – а.2 / (2А0 ) . |
(4.223) |
4 |
|
Отсюда видно, что, как и должно быть для фазовых переходов второго рода, Gm и ее первая производная в точке перехода изменяются непрерывно, а вторая производная – скачкообразно. Энтропия упорядоченного сплава S = –∂( Gm)/∂T будет равна
S= So – а.2(TK – T)/ (2А40 ) ,
где So= – ∂ G0/∂T. Скачок теплоемкости ср = Т(∂S/∂T)p, соответствующий переходу из упорядоченного в неупорядоченное состояние, при T = TK равен:
cp = cp TK −0 − cp TK +0 =a2TK /(2A40 ) .
Таким образом, скачок теплоемкости является конечным, при-
чем, поскольку |
А0 |
> 0, ср > 0. Следовательно, при переходе в |
|
4 |
|
упорядоченное состояние теплоемкость всегда увеличивается. Не представляет трудностей рассчитать скачки так же и других величин.
Теперь получим концентрационную зависимость степени дальнего порядка при постоянных T и p вблизи TK . Для этого продифференцируем α2 из (4.220), рассматриваемую как функцию Т и xA
197
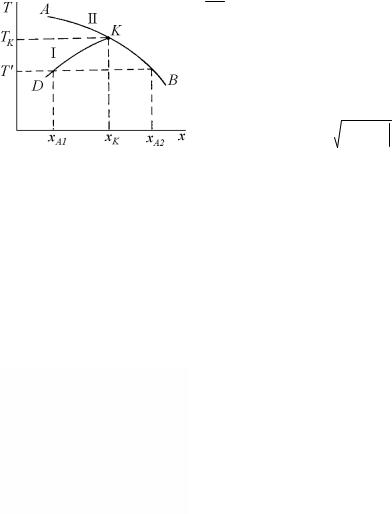
вдоль кривой фазового перехода в плоскости {T, xA} при постоянном p:
∂α2 = a ∂TК .
∂xA A40 ∂xA
Интегрируя последнее выражение по хА от x0A до хА при условии, что при хА = x0A степень дальнего порядка α = 0, получаем:
α2 = |
a |
|
∂TК |
(x |
|
− x0 ) . |
|
A0 |
|
||||||
|
|
∂x |
A |
|
A |
A |
|
|
4 |
|
|
|
|
|
|
Следовательно, при малых (хА – x0A ) имеем: α ≈ 
 xA − x0A .
xA − x0A .
Кривая фазовых переходов второго рода не может окончиться в некоторой точке плоскости {T, х}. Это связано с тем, что линия точек фазовых переходов второго рода разделяет области существования фаз с различной симметрией, между которыми не может быть непрерывного перехода, т.к. симметрия не может непрерывно изменяться. В упорядочивающихся твердых растворах линия точек фазовых переходов второго рода в некоторой точке, называемой
критической точкой переходов второго рода, может переходить в кривую распада, которая является линией фазового перехода первого рода.
Диаграмма состояния в плоскости {T, х} вблизи такой точки изображена на рис. 4.44. Здесь АK – линия точек фазового перехода второго рода, которая в критической точке K переходит в кривую распада KВ. Выше кривой АВ расположена область II неупорядоченной фазы. Область I соответствует области существования упорядоченной фазы, а область между кривыми KВ и KD является двухфазной областью. Таким образом, при Т = = Т′ для состояний, находящихся в этой области, сплав распадается на
198
упорядоченную фазу состава хА1 и неупорядоченную фазу состава
хА2 .
4.9.3.Статистическая теория упорядочения
Вотличие от термодинамической теории в статистической теории используется конкретная атомная модель сплава, определяющая выражение для свободной энергии, откуда и находятся равновесные свойства системы. Входящие в статистическую теорию энергетические параметры могут быть связаны как с энергиями взаимодействия атомов, так и с величинами, характеризующими структуру сплава. При этом удается получить результаты, справедливые во всей области изменения степени дальнего порядка и состава. Более того, статистическая теория позволяет исследовать не только дальний, но и ближний порядок, если определить температурную и концентрационную зависимость параметров корреляции
вразличных координационных сферах.
Врассматриваемой статистической теории упорядочения, как и ранее, используется приближенная модель парного взаимодействия атомов, основанная на предположении, что энтальпию и энтропию образования (смешения) сплава можно представить в виде конфигурационного вклада, зависящего от расположения атомов.
Вэтом случае конфигурационная свободная энергия смешения сплава по Больцману выражается как
GKM = H KM −T SKM = H KM − kT lnWK , |
(4.224) |
где WK – число различных способов пространственного размещения атомов, необходимых для реализации данного макросостояния. В данном параграфе индексы «K» при величинах означают учет только конфигурационных вкладов.
Наиболее простым методом расчета свободной энергии является квазихимический метод, согласно которому учитываются взаимодействия только ближайших соседей. Квазихимический метод дает возможность удовлетворительного объяснения ряда явлений, происходящих в упорядочивающихся сплавах.
Рассмотрим конфигурационную энтальпию бинарного твердого раствора замещения А-В. Обозначим соответственно через εАА, εВВ и
199
εАВ энергии взаимодействия (связи) пар атомов А-А, В-В и А-В, а количество пар атомов (или число связей) на один г-атом раствора
– через NАА, NВВ, NАВ. В этих обозначениях
H KM = NАА εАА+ NВВ εВВ +NАВ εАВ . |
(4.225) |
Если z – координационное число для первой координационной сферы, то количество атомов сорта А и В, занятых в указанных парах, можно вычислить следующим образом:
N A = |
N |
AB |
+ |
2N |
AA |
|
|
|
, |
||||
z |
z |
|
||||
|
|
|
|
|||
NB = |
N AB |
+ |
2NBB |
|
||
|
|
|
|
. |
||
z |
z |
|
||||
|
|
|
|
|||
Отсюда NАА |
и NВВ можно выразить через NА, NВ, NАВ и z: |
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
N AA |
= |
|
|
(zN A − N AB ), |
|
|
|||
|
|
|
2 |
|
(4.226) |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
NBB |
= |
|
|
(zNB − N AB ). |
|
|
|||
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
Подставляя (4.226) в (4.225), получим: |
|
|
||||||||||
M |
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
H K |
= |
|
N A zεAA + |
|
NB zεBB + N AB εAB − |
|
(εAA + εBB ) . |
|||||
2 |
2 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
||||
Первые два члена этого соотношения представляют энтальпии чистых компонентов А и В и, следовательно, последний член пред-
ставляет теплоту смешения раствора: |
|
|
|||
M |
|
1 |
|
|
|
H K |
= N AB εAB − |
|
|
(εAA + εBB ) . |
(4.227) |
2 |
|
||||
|
|
|
|
|
|
Рассмотрим упорядочение в бинарном сплаве А-В, имеющем одинаковое число N/2 узлов первого и второго типа, причем каждый узел данного типа окружен только узлами другого типа. Ограничимся случаем сплавов типа β-латуни с объемноцентрированной кубической решеткой и координационным числом для первой координационной сферы z = 8. Корреляцию в сплаве учитывать не будем.
В указанном приближении число пар соседних разноименных атомов NАВ равно произведению вероятности пары А-В на общее число пар атомов в сплаве zN/2. Вероятность пары А-В складывает-
200
ся из произведения априорных вероятностей (в приближении, не учитывающем корреляцию) РA(1) РB(2) и. РB(1) РA(2) . Эта вероятность
соответствует ситуации, когда разноименные пары образуются из атомов сорта А, находящихся на узлах первого типа, и атомов В, находящихся на узлах второго типа, а так же из атомов А, находящихся на узлах второго типа, и атомов В, находящихся на узлах первого типа, т.е. на «чужих» узлах. Таким образом,
NАВ = zN( Р(1) |
Р(2) |
+ Р(1) |
Р(2) |
)/2 . |
(4.228) |
A |
B |
B |
A |
|
|
Используя выражение априорных вероятностей из (4.209), име-
ем: |
|
NАВ = zN [2xAxB(1 – α + α2) + α(x2A + x2B)]/2, |
(4.228а) |
а для рассматриваемой структуры стехиометрического состава при
хА = хВ = ½ и z = 8 |
|
NАВ = 2N(1 + α2), |
(4.228б) |
что позволяет получить для H KM в соответствии |
с формулой |
(4.227) следующее выражение: |
|
HKM = 2N(1 + α2) .Δε, |
(4.229) |
где Δε = [εАВ – ( εАА + εВВ)/2].
Величина WK в выражении (4.224) есть вероятность состояния, в котором NА атомов А и NB атомов В распределены между «своими» и «чужими» узлами, выражающаяся как произведение вероятностей W(1) и W(2), соответствующих числу способов распределения заданного числа и типа атомов на узлах первого и второго типа.
Так как W (i) = (N 2!)/(N A(i)!NB(i)!), |
получаем следующее выражение |
|||||||||||||
для WK : |
|
|
|
(N |
|
)! |
|
|
(N |
|
)! |
|
|
|
|
(1) |
(2) |
|
2 |
|
|
2 |
|
|
|
||||
WK = |
W W |
|
= |
|
|
|
|
|
|
|
|
|
. |
(4.230) |
|
N A(1)!NB(1) |
|
N A(2)!NB(2) |
|
||||||||||
|
|
|
|
! |
! |
|
||||||||
Подставляя в (4.230) выражения (4.206) и (4.209) с учетом
N(1) = N(2) = N/2 и хА = хВ = 1/2,
и используя приближение Стирлинга, получим:
SKM = k.lnWK = |
|
= R{ln2 – [(1 + α)ln(1 + α) + (1 – α)ln(1 – α)]/2}. |
(4.231) |
201

В пределе при α → 0, SKM → R·ln2, что представляет энтро-
пию полностью неупорядоченного раствора.
Таким образом, конфигурационная свободная энергия смешения (4.224) в рассматриваемом приближении имеет вид функции Т и α :
|
GKM = 2N (1+ α2 ) E − |
||
− RT{ln 2 − |
1 |
(4.232) |
|
[(1+ α)ln(1+ α) +(1− α)ln(1− α)]}. |
|||
2 |
|||
|
|
||
Равновесное значение степени дальнего порядка α можно найти
из условия равновесия ∂ GKM ⁄∂α = 0: |
|
|
|
||
4Δεα + |
kT |
ln |
1+ α |
= 0. |
(4.233) |
|
1− α |
||||
2 |
|
|
|
||
Критическая температура перехода ТK |
определяется из (4.233) |
||||
как предельная при α → 0. В простейшем приближении можно разложить второй член выражения (4.233) по степеням α и при малых значениях α ограничиться лишь членами первого порядка:
|
|
1 + α |
2α , |
(4.233а) |
|
lim |
ln |
|
|
||
|
|||||
α→0 |
|
1 − α |
|
|
|
так как
+(x −1)3
x +1 3(x +1)3
Вэтом случае из (4.233) получаем для регулярного раствораln x = 2 x −1 +..... .
T |
= − |
4 E |
или |
T = − |
Ω |
. |
(4.234) |
|
|
||||||
K |
k |
|
K |
2R |
|
||
|
|
|
|
|
|||
Таким образом, в рамках использованной модели получаем, что величина ТK зависит от соотношения между энергиями парного взаимодействия атомов, а дальний порядок может иметь место только в случае εАВ < (εАА+εВВ)/2, что соответствует наиболее стабильному состоянию, когда атомы одного сорта окружены преимущественно атомами другого сорта. Величина Δε в этом случае играет роль энергии упорядочения.
Подставляя значение Ε из (4.234) в выражение (4.233), получаем следующий приближенный вид температурной зависимости степени дальнего порядка (рис. 4.45):
202

|
T |
|
1 |
+ α |
|
1+ α |
|
T |
||||
2α |
K |
= ln |
|
|
|
или |
|
|
|
= exp 2α |
K |
. (4.235) |
|
T |
|
1 |
−α |
|
1 |
− α |
|
T |
|||
Использование в разложении (4.233а) кубических членов позволяет из (4.235) получить температурную зависимость α в виде
|
T |
|
|
|
|
α3 |
|
|
|
2α |
K |
|
|
2 |
α + |
|
|
|
|
|
|
|
|||||||
|
T |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
или |
|
|
|
|
|
|
|
||
α2 = |
T |
|
|
|
|
|
|||
3 |
K |
|
−1 , |
(4.236) |
|
||||
T |
|
|
|||||||
|
|
|
|
|
|
|
|
Рис. 4.45. Температурная |
|
согласующуюся с |
результатом (4.220) |
зависимость степени дальнего |
|||||||
термодинамической теории упорядоче- |
порядка α для сплавов |
||||||||
со стехиометрией АВ и z = 8 |
|||||||||
ния. |
|
|
|
|
|
|
|
||
Приведенная на рис. 4.45 температурная зависимость α удовлетворительно согласуется с экспериментальными данными для конкретных структур. Дальнейшее улучшение модели заключается в использовании статистических теорий, учитывающих корреляцию в сплавах. Как следует из рис. 4.45, α близка к единице при низких температурах и быстро уменьшается только при Т → ТK. Эта особенность типична для явлений, в которых участвуют большие группы атомов, что соответствует принадлежности фазовых переходов при упорядочении к непрерывным превращениям.
Из вида выражения (4.231) следует, что энтропия изменяется непрерывно при переходе через критическую точку ТK, соответствующую в формуле (4.231) переходу от α < 0 к α > 0 через α = 0. Следовательно, теплота перехода равна нулю, и в рассматриваемой структуре превращение порядок–беспорядок является фазовым переходом второго рода. Скачок теплоемкости при этом переходе может быть рассчитан следующим образом
cp = cp T <TK − cp T >TK ,
где индексы Т < TK и Т > ТK означают проведение оценки ср при α > 0 и α = 0, соответственно.
Используя выражения (4.229), (4.234) и (4.236), получаем
203
|
|
|
|
∂ |
H M |
|
|
∂α2 |
|
3 |
|
T |
2 |
||
|
|
|
|
|
|
|
|||||||||
cp |
|
|
|
|
K |
|
= 2NA ε |
|
|
= |
|
NA k |
K |
||
|
|
|
|
|
|
||||||||||
T <T |
|
= |
|
∂T |
|
∂T |
2 |
T |
2 . |
||||||
|
|
K |
|
|
P |
|
|
|
|
|
|||||
Учитывая, что при α = 0, |
∂α2/∂Τ = 0 , при Т → ТK получаем |
||||||||||||||
|
|
|
|
|
cP = |
3 |
NA k = |
3 |
R , |
|
|
|
|
||
|
|
|
|
|
2 |
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
что соответствует конечному скачку конфигурационной теплоемкости при фазовых переходах второго рода.
В рамках тех же предположений можно проиллюстрировать решение задачи упорядочения для сплавов, у которых числа узлов первого и второго типа являются неодинаковыми, например, для сплавов с гранецентрированной кубической решеткой типа АВ3. Будем считать, что узлами, предназначенными для атомов А, являются вершины кубических ячеек, а для атомов В – центры их граней. В этом случае узлов первого типа в три раза меньше, чем второго, и их концентрация ν = 1/4. Координационное число для первой координационной сферы z = 12, причем каждый узел первого типа окружен двенадцатью соседними узлами второго типа, а узел второго типа среди своих ближайших соседей имеет четыре узла первого типа и восемь узлов второго типа. Число пар АВ в этом случае определяется следующим образом:
N |
AB |
=12 |
N |
Р(1) |
Р(2) |
+ 4 |
3N |
Р(2) Р(1) |
+8 |
3N |
Р(2) |
Р(2) = |
||||
|
|
|
||||||||||||||
|
4 |
A |
B |
|
4 |
|
A |
B |
|
4 |
A |
B |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
= 3N(Р(1) Р(2) + Р(2) |
Р(1) + 2Р(2) Р(2) ). |
|
||||||||||||
|
|
|
|
|
A |
B |
A |
B |
|
|
A |
B |
|
|
|
|
Используя (4.227) с учетом (4.209) получаем для |
H KM : |
|||||||||||||||
|
|
|
|
|
H KM |
= 3/4NΔε(3+α2). |
|
|
(4.237) |
|||||||
Число перестановок атомов на узлах решетки |
при заданной |
|||||||||||||||
степени дальнего порядка α в сплавах указанного типа равно |
||||||||||||||||
|
|
WK =W (1)W (2) = |
(N / 4)! |
|
|
(3N / 4)! |
. |
|||||||||
|
|
N A(1)! NB(1) |
|
|
||||||||||||
|
|
|
|
|
|
|
! |
N A(2)! NB(2)! |
|
|||||||
Аналогично тому, как это было сделано при выводе формулы (4.232), можно найти свободную энергию смешения для сплава:
GKM = HKM − kT lnWK ,
204

и из условия ∂ GKM / ∂α = 0 получить следующее уравнение для
определения равновесных значений степени дальнего порядка в виде:
Рис. 4.46. Температурная зависимость степени дальнего порядка α для сплавов со стехиометрией АВ3 при z = 12
ln |
|
3(1− α)2 |
= |
8 |
ε |
α. |
|
(3 |
+ α)(3α +1) |
kT |
|||||
|
|
|
|||||
Выражаемая этим уравнением температурная зависимость α изображена на рис. 4.46.
Полученное уравнение при достаточно низких температурах кроме тривиального решения α = 0 имеет и другие действительные корни, отличные от нуля. Анализ поведения семейства кривых
GKM (α) для различных темпера-
тур показывает, что участок кривой а–b на рис. 4.46 соответствует возможным равновесным упорядоченным состояниям сплава, участок b–с соответствует равновесию упорядоченной и неупорядоченной метастабильной фаз, участок с–d соответствует максимуму
GKM (α) – неустойчивому состоянию, которое не может сущест-
вовать с такими значениями α.
Температура перехода ТK и соответствующее ей значение αK могут быть определены из системы уравнений:
GKM (αK ) = |
GKM (0), |
|||
∂ GKM |
|
|
|
|
|
|
|
||
|
|
= 0. |
. |
|
∂α |
|
|
|
|
|
|
|
||
α=α |
K |
|
|
|
|
|
|
|
|
Численное решение этой системы для сплава AuCu3, имеет вид
T |
= − |
0,82 ε |
и α |
K |
= 0,46 , |
|
|||||
K |
|
k |
|
|
|
|
|
|
|
|
что качественно согласуется с экспериментальными результатами. Подставляя полученное значение αK в (4.237), можно убедиться, что теплота перехода отлична от нуля, а так же рассчитать скачок
205
энтропии. Следовательно, упорядочение в сплаве AuCu3 является фазовым переходом первого рода.
Следует отметить, что статистическая теория упорядочения, не учитывающая корреляцию в сплавах, в некоторых случаях дает даже качественно неправильные результаты. Так, расчет в рамках использованной выше модели для сплавов с гранецентрированной решеткой с равным числом атомов первого и второго типа, например для AuCu, не дает возможности получить фазовый переход первого рода и приводит к результату аналогичному полученному выше для β-латуни.
4.9.4. Kвазихимическая трактовка ближнего порядка
Согласно современным представлениям физики твердого тела, основным в упорядочении атомной структуры твердого раствора является стремление к установлению ближнего порядка. Это стремление проявляется при любых температурах независимо от того, устанавливается в кристалле дальний порядок или нет. Более того, это стремление проявляется не только в кристаллическом, но и в жидком состоянии, где возникновение дальнего порядка принципиально невозможно. Так как силы взаимодействия между атомами быстро убывают с увеличением расстояния между ними, естественно считать, что энергия образования твердого раствора слагается почти целиком из взаимодействия ближайших разноименных соседних атомов, приводящего к образованию областей ближнего порядка уже в жидком расплаве. Размеры этих областей увеличиваются с понижением температуры, особенно после кристаллизации и переходе в твердое состояние. Образование дальнего порядка можно представить себе как когерентное слияние областей ближнего порядка.
В квазихимическом смысле для ближнего порядка характерно больше, чем беспорядочное, число разноименных связей NAB. Для количественного решения проблемы степень ближнего порядка может быть представлена в виде (4.210). Рассчитаем температурную зависимость степени ближнего порядка в рамках статистиче-
206
ской теории без учета корреляции для первой координационной сферы ОЦК структуры с равным числом атомов А и В.
Используя выражения (4.210), (4.212) и (4.213) с учетом того, что здесь z1 = 8 и хА = хВ = ½, для конфигурационной теплоты смешения в соответствии с (4.142) можно получить:
H KM = NAB ·[εAB –1/2 (εAA + εBB)] =
=2N(1 + σ)·[εAB –1/2(εAA + εBB)],
аWK в выражении (4.224) или (4.231) можно получить, как число
способов реализации конфигурации со степенью ближнего порядка σ, равное числу сочетаний из zN/2 возможных пар по разноименным NAB и одноименным NAA и NBB парам:
WK = |
(Nz / 2)! |
|
. |
(4.238) |
|
(N AB )!(N AA + NBB )! |
|||||
|
|
|
|||
Подставляя в (4.238) значения NAB, рассчитанные по формуле (4.213) и NAA и NBB из (4.226), определяем значение конфигураци-
онной свободной энергии в соответствии с (4.224): |
|
|
||||
GKM = 2N(1+ σ) ε − kTln |
|
(4N )! |
|
. |
(4.239) |
|
[2N (1 |
+ σ)]![2N(1− σ)]! |
|||||
|
|
|
||||
Используя приближение Стирлинга можно найти равновесное значение степени ближнего порядка σ из условий равновесия
ln |
1 |
+ σ |
= − |
ε |
или |
1+ σ |
= exp(− |
ε |
) . |
(4.240) |
1 |
− σ |
kT |
1− σ |
|
||||||
|
|
|
|
kT |
|
|||||
Для того чтобы избежать громоздких вычислений, связанных с использованием факториальной техники, аналогичный результат для рассматриваемой конкретной ситуации можно получить с помощью простейших рассуждений. Предположим, что из общего
количества |
связей |
zN/2 доля |
связей |
типа А-В составляет |
|||
fAB = |
NAB |
= 12 (σ +1) . |
Следовательно, доля связей одноименных |
||||
12 zN |
|||||||
|
|
|
|
|
|
||
атомов равна 1− f AB = 12 (1− σ) . |
|
|
|||||
Предположим, |
что |
средняя |
энергия |
одноименных связей |
|||
(εАА+εВВ)/2 больше, чем εАВ для разноименных, т.е. когда Δε < 0. Покажем, что в этом случае будет иметь место ближний порядок.
207
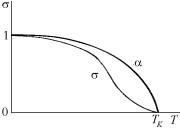
|
|
|
ε |
i |
|
Так называемый фактор Больцмана |
exp |
− |
|
дает вероятность |
|
|
|
||||
|
|
|
kT |
||
занятости состояния с энергией εi. Следовательно, отношение вероятностей занятости состояний W2/W1, которое является отношением вероятностей связей разноименных и одинаковых атомов или долей общего количества соответствующих связей fij/fii, равно:
W |
|
fij |
|
ε |
|
|
1+ σ |
|
ε |
|
|||||
|
2 |
= |
|
|
= exp(− |
|
) |
или |
|
|
|
= exp(− |
|
) , |
|
W |
f |
ii |
kT |
1 |
− σ |
kT |
|||||||||
|
|
|
|
|
|
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
что полностью совпадает с полученным выражением (4.240). Анализ (4.240) показывает: если Δε < 0, то σ > 0, что указывает
на существование ближнего порядка. Если Δε > 0, то σ < 0 и это приводит к образованию обособленных группировок атомов (или комплексов), т.е. к образованию ближней сегрегации однородных атомов или ближнего распада твердого раствора. Если размеры областей ближнего порядка увеличиваются, то наступает «дальний распад», когда идет образование двух твердых растворов разных концентраций или в пределе – двух чистых компонентов.
Следует отметить, что сравнение величины и вида температурной зависимости параметров ближнего и дальнего порядков лишено физического смысла, если расчеты в рамках статистической теории проводятся без учета корреляции. Если сравнить, например, значение σ, рассчитанное по формуле (4.210) с использовани-
ем NAB, выраженного через степень дальнего порядка α с помощью (4.228б), то для стехиометрического сплава АВ с ОЦК ре-
2 |
Рис. 4.47. Температурная зависимость |
шеткой получим, что σ = α . Это |
степени ближнего σ и дальнего α |
означает, что при отсутствии |
порядка для сплавов стехиометриче- |
дальнего порядка в системе дол- |
ского состава АВ при z = 8 |
жен отсутствовать и ближний |
без учета корреляции |
(рис. 4.47).
Для большинства же реальных систем экспериментальные данные свидетельствуют о том, что при α = 0 степень ближнего поряд-
208
ка не равна нулю и, более того, ближний порядок сохраняется и при T > TK.
4.9.5.Системы с промежуточными фазами
Втеории упорядочения были фактически рассмотрены системы
сне очень большими отрицательными значениями параметра взаи-
модействия, т.е. когда |Ω| ≈ RT. Упорядоченный твердый раствор имеет ту же кристаллическую структуру, что и чистые компоненты. Но его уже можно рассматривать как прообраз химического соединения, причем допускающего неограниченное отклонение от стехиометрии, поскольку границы области упорядочения достаточно размыты. Вид диаграммы состояния с упорядочением будет примерно такой, как показано на рис. 4.29,а – две сигары с максимумом.
Как известно, природа фаз определяется особенностями межмолекулярного взаимодействия, которое, в первую очередь, обусловлено сортами частиц, их образующих. Ведь именно от природы частиц зависит величина и характер сил обменного взаимодействия. Это приводит к формированию вполне определенных химических связей. Если растворы и фазы различаются родом образующих их частиц (по сортности), то, следовательно, их химические составы (речь идет об истинных составах) качественно различны. Следствием этого является то, что термодинамические характеристики фаз, различающихся родом частиц, описываются разными фундаментальными уравнениями. Это очень важное заключение с необходимостью приводит к выводу о том, что такие растворы даже в пределах одной гомогенной системы должны рассматриваться как самостоятельные фазы.
Различие между зависимостями свойств растворов, имеющих качественно иные химические составы, от параметров состояния должно проявляться если не в виде самих функций, то, по крайней мере, в значениях констант, фигурирующих в уравнениях этих функций и отражающих специфику межчастичного взаимодействия, а, следовательно, и химическую природу сравниваемых растворов. В случае растворов или фаз переменного состава данному
209
качественному составу или, иначе говоря, данному набору частиц по сорту отвечает конечный интервал количественных составов в данной системе, в пределах которого только и существует строго определенный единственный вид зависимости термодинамических и иных свойств от параметров состояния.
Положение о том, что характер зависимости свойств от параметров состояния определяется качественным химическим составом, весьма существенно. А.В. Сторонкин назвал его принципом качественного своеобразия определенных химических соединений. Значение принципа заключается в том, что его использование позволяет четко определить принадлежность растворов на основе определенных химических соединений к самостоятельным фазам, а это, в свою очередь, позволяет более строго использовать метод графической термодинамики при установлении общего характера фазового равновесия в системе с наличием промежуточных фаз.
Очевидно, образование промежуточных твердых фаз в двухкомпонентной системе так же должно внести самостоятельный элемент в диаграмму состояния. Как правило, промежуточные твердые фазы формируются на основе определенных химических соединений, которые могут плавиться конгруэнтно (без разложения) или распадаться в результате перитектического превращения. Обсуждение характера концентрационной зависимости изобарноизотермического потенциала промежуточных фаз следует вести в соответствии со строго термодинамически обоснованным понятием фазы. При этом требуется уточнение принадлежности растворов на основе существующих в системе определенных химических соединений к одной или разным фазам.
Итак, если в системе образуется устойчивое недиссоциирующее химическое соединение АmВn то очевидно, что растворы, образованные путем добавления компонента А к AmBn и В к АmВn следует относить к различным фазам независимо от агрегатного состояния системы. В данном пункте мы приходим к важному выводу о том, что в результате взаимодействия между компонентами А и В образовалось химическое соединение AmBn, отличающееся собственной (как правило, совершенно иной в сравнении с А и В) кристаллической структурой, если речь идет о твердом состоянии, и собствен-
210
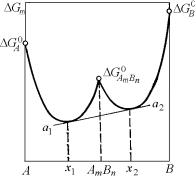
ной особой структурой ближнего порядка, если речь идет о жидком состоянии, а так же собственным характером химической связи. На основании этого устойчивое химическое соединение в двухкомпонентной системе следует рассматривать как самостоятельный компонент, расчленяющий данную систему на отдельные подсистемы.
Заметим, что на этом выводе базируется дальнейшее рассмотрение фазовых соотношений в системах с промежуточными фазами на основе определенных химических соединений. Замечательно, что к этому заключению пришел Д.И. Менделеев, рассматривавший возможность образования химических соединений в растворах. Он подчеркивал, что «растворы разбиты, расчленены определенными соединениями, если среди растворов они находятся».
В свете изложенного рассмотрим жидкий раствор, в котором образуется недиссоциирующее соединение АmВn. Так как согласно принятому положению это соединение рассматривается как компонент при каждой данной температуре, оно характеризуется самостоятельным значением изобарно-изотермического потенциала. Растворы А-АmВn и АmВn-В, следовательно, являются самостоятельными фазами. На этом основании общий характер изменения изо- барно-изотермического потенциала от брутто-состава жидкого раствора определится уже w-образной кривой с угловой точкой (рис. 4.48).
Рис. 4.48. Концентрационная зависимость изобарно-изотермического потенциала в системе
с устойчивым недиссоциированным соединением AmBn в жидкой фазе
Таким образом, каждая частная система, имея свою жидкую фазу, характеризуется собственной кривой зависимости Gm(x), которая в соответствии с установленными выше закономерностями
211
всюду обращена выпуклостью к оси составов. При этом, очевидно, отпадает вопрос о возможности проведения общей касательной к двум указанным кривым, поскольку они принадлежат, по существу, разным системам, и только для наглядности и характеристики системы А-В в целом изменение изобарно-изотермичес- кого потенциала дано в функции брутто-состава, т. е. в зависимости от молярной доли компонента В.
Даже незначительная диссоциация соединения AmBn в корне изменяет положение дел. Качественный молекулярный состав слева от ординаты соединения перестает в принципе отличаться от состава справа от нее, и в итоге будем иметь одну жидкую фазу, концентрационная зависимость изобарно-изотермического потенциала которой должна описываться кривой, показанной на рис. 4.24. При этом нет нужды обсуждать вопрос о возможности проведения общей касательной к кривым, представленным на рис. 4.48. Очевидно, что нет необходимости специально обсуждать вопрос о правомерности перенесения указанных рассуждений на твердое состояние, поскольку принципиальной разницы между жидкими и твердыми растворами нет.
Опираясь на изложенные выше общие положения, касающиеся систем с недиссоциирующими соединениями, а так же растворов на их основе, мы можем перейти к конкретному рассмотрению двух принципиально различающихся типов диаграмм состояния с химическими соединениями. Различие заключается в том, что в одном случае соединения устойчивы вплоть до температуры плавления и переходят в жидкую фазу того же состава, т. е. плавятся конгруэнтно, а в другом случае соединения принимают участие в трехфазном перитектическом превращении в качестве промежуточной фазы, т. е. плавятся инконгруэнтно.
Конгруэнтно плавящиеся соединения при условии отсутствия диссоциации в твердом и жидком состоянии разделяют двойную систему А-В на соответствующее число подсистем, в пределах которых фазовое равновесие может быть представлено одним из видов простых диаграмм состояния. На рис. 4.49 представлена диаграмма состояния системы с устойчивым конгруэнтноплавящимся соединением АmВn, которое при взаимодействии с компонентами А
212
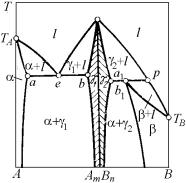
и В образует частные системы. Картина может усложняться за счет возможного расслаивания в жидкой фазе частной системы, а так же за счет полиморфизма как у компонентов А и В, так и у соединения
АmВn .
Устойчивость соединения АmВn в твердом и жидком состоянии подчеркнута сингулярным характером максимума в точке плавления, соответствующей стехиометрическому составу, где сходятся ветви кривых ликвидуса и солидуса граничных частных систем.
В полном соответствии с изложенным относительно формирования диаграмм состояния частных систем типа А-АmВn и АmВn-В из рис. 4.49 следует заключить, что образующиеся на основе соединения АmВn твердые растворы компонентов А и В суть различные фазы, а не одна γ-фаза, как это часто изображают в различных руководствах по фазовым равновесиям. Естественно, что эти растворы сформированы на базе одной кристаллической решетки соединения AmBn и, следовательно, являются изоморфными. Известно немало примеров, когда в системах эвтектического типа твердые растворы на основе компонентов имеют однотипные кристаллические структуры (например, система медь–серебро), однако совершенно очевидно, что их следует считать различными фазами. В данном случае, если последовательно использовать принцип качественного своеобразия химических соединений, приходим к выводу, что область гомогенности на основе устойчивого соединения слагается из двух областей, отвечающих двум хотя и изоморфным, но все же различным фазам, разграниченным друг относительно друга ординатой химического соединения.
Если соединение АmВn частично диссоциировано в жидкой фазе, то кривая ликвидуса в точке максимума несколько сглажена, причем степень диссоциации находится в прямой связи с радиусом
213

кривизны ликвидуса. При этом соединение АmВn уже не делит жидкий раствор на две различные фазы в рамках единой гомогенной системы и в результате имеется только одна жидкая фаза во всей системе А-В. Это следует учитывать при соответствующих построениях с помощью метода графической термодинамики. В случае диссоциации соединения AmBn не только в жидком, но и в твердом состоянии сглаженный максимум будет так же и на кривой солидуса, причем так же, как и в случае жидкого состояния, величина радиуса кривизны будет характеризовать степень диссоциации соединения. Следует при этом иметь в виду, что в случае существенной диссоциации соединения максимум на диаграмме состояния может быть сдвинут относительно стехиометрического соотношения компонентов. Вполне очевидно, что на основе частично диссоциированного в твердом состоянии соединения формируется только одна, а не две фазы, как в случае соединения недиссоциированного. На рис. 4.50 показаны виды максимумов на кривых ликвидуса и солидуса, характеризующие различные варианты сочетания этих кривых в случае наличия или отсутствия диссоциации соединения AmBn в твердом и жидком состоянии. Однако независимо от вида максимума общий характер фазового равновесия в системе с промежуточной фазой определяется характером ее взаимодействия с компонентами в твердом и жидком состоянии, а следовательно, и видом возникающих трехфазных равновесий.
Рис. 4.50. Виды максимумов на кривых ликвидуса и солидуса при наличии в системе А–В соединения AmBn в зависимости от его термической устойчивости в твердом и жидком состояниях
В случае образования химического соединения по перитектической реакции общий принцип обоснования фазовых соотношений в окрестности перитектической горизонтали ничем не отли-
214
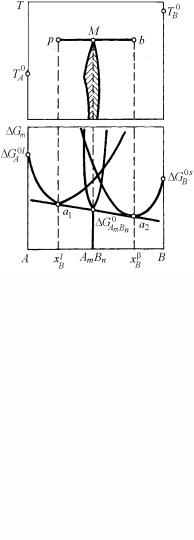
чается от простой перитектической системы, которая была рассмотрена ранее.
Учитывая наличие твердого раствора на основе компонента А и соответствующего двухфазного равновесия α ↔ L , возникает проблема сочетания последнего со стабилизирующимся при охлаждении ниже температуры перитектической горизонтали двухфазным равновесием с участием фазы на основе соединения AmBn. Возникающие при этом трехфазные равновесия могут быть различными.
На рис. 4.51 показана одна из возможных диаграмм состояния с инконгруэнтно плавящимся соединением AmBn. Рассматривая возможность обоснования такой диаграммы при помощи кривых зависимости изобарно-изотермического потенциала от концентрации, необходимо иметь в виду, что на основе соединения образуется либо одна, либо две фазы, а следовательно, и при графических построениях следует использовать соответствующее числу фаз количество кривых Gm(x). Иными словами, при термодинамическом обосновании систем, типа показанной на рис. 4.51, следует учитывать принцип качественного своеобразия определенных химических соединений.
Заметим, что формирование в процессе перитектического пре-
215
вращения устойчивого соединения AmBn стехиометрического состава дает основание считать, что ниже перитектической горизонтали оно играет роль компонента со всеми вытекающими отсюда последствиями. В частности, при температуре перитектики равновесие фаз может быть обосновано путем проведения общей касательной через точку, отвечающую значению изобарно-изотермического потенциала соединения AmBn, к кривым концентрационной зависимости его для жидкой фазы L и твердой фазы β так, как это показано на рис. 4.52. Далее, проецируя составы, отвечающие точкам касания, к температуре Тр на диаграмме состояния, получим фиксированные положения фаз, находящихся при этой температуре в равновесии совместно с соединением AmBn.
Рассмотренный на рис. 4.52 вариант образования определенного соединения непосредственно в процессе перитектической реакции характерен именно для данного соотношения между температурами плавления компонентов и трехфазного равновесия. Естественно, что это соотношение может быть и иным, однако в принципе ход рассуждений будет точно таким же.
Контрольные вопросы
1.Что такое термодинамические системы? Дайте их определение, а так же поясните понятия «состояние», «параметр», «процесс».
2.Что можно вложить в основное термодинамическое понятие «термодинамическое равновесие»?
3.Термодинамический процесс. Является ли он объектом термодинамического исследования?
4.Самопроизвольные и несамопроизвольные процессы. В чем их различие?
5.Принцип Ле Шателье–Брауна. Как его можно использовть при термодинамическом методе исследованя?
6.Покажите преимущества и ограничения термодинамического метода.
7.Что такое «моль вещества»?
8.Внутренняя энергия. Дайте определение и покажите условность отсчета внутренней энергии.
9.Дайте определение функции состояния.
216
10.Сформулируйте первый закон термодинамики в дифференциальной форме.
11.Сформулируйте второй закон термодинамики через температуру.
12.Что обычно понимается под термодинамическими переменными? Независимые переменные. Число независимых переменных.
13.Напишите уравнение состояния идеальных газов.
14.Дайте определение энтальпии. Напишите ее полный дифференциал.
15.Дайте определение энтропии как приведенной теплоты (по Клаузиусу).
16.Дайте вероятностную и статистическую трактовку энтропии.
17.Сформулируйте третье начало термодинамики – тепловую теорему Нернста.
18.Что происходит с энтропией при самопроизвольных, необратимых процессах в изолированной системе?
19.Чем различаются равновесные и неравновесные процессы?
20.Сформулируйте второй закон термодинамики, используя понятие энтропии.
21.Сформулируйте принцип максимума энтропии как второй закон термодинамики.
22.Что понимается под экстенсивными и интенсивными величинами? Приведите примеры.
23.Что понимается под внутренними параметрами? Приведите примеры.
24.Как осуществить формализованный поиск условий равновесия в изолированной системе?
25.Сформулируйте необходимые и достаточные условия равновесия.
26.Перечислите свойства потенциальных функций.
27.Что понимается под естественными переменными?
28.Есть ли различие между понятиями «функция состояния» и «характеристическая функция»?
29.Есть ли различие понятий «характеристическая функция» и «термодинамический потенциал»?
30.Дайте определение и напишите полный дифференциал потенциала Гиббса.
31.Что понимается под характеристическими функциями?
32.Укажите экстремальные свойства термодинамических потенциа-
лов.
33.Химический потенциал. Дайте его определение и раскройте физический смысл.
217
34.Какова связь химического потенциала и потенциала Гиббса?
35.Напишите фундаментальные уравнения Гиббса.
36.Является ли теплоемкость при постоянном давлении истинной физической характеристикой тела как физического вещества?
37.Как соотносятся теплоемкости по величине: Ср >CV или CV >Ср?
38.Почему теплоемкость кристаллического тела при абсолютном нуле температуры равна нулю?
39.Почему теплоемкость аморфного тела при абсолютном нуле температуры не равна нулю?
40.Каков общий вид зависимости теплоемкости от температуры?
41.Каков физический смысл характеристической температуры Дебая θ для твердых тел?
42.Каков физический смысл характеристической температуры Эйн-
штейна ε/k для газов?
43.Каков принципиально вид зависимости энтропии от температуры? Докажите.
44.Каков принципиально вид зависимости энтальпии от температуры? Докажите.
45.Каков принципиально вид зависимости изобарно-изотермического потенциала от температуры? Докажите.
46.Как зависит от температуры приведенный потенциал Гиббса?
47.Каков вид зависимости энтропии газов от давления?
48.Как зависит энтропия конденсированных тел от давления?
49.Как зависит энтальпия веществ от давления?
50.Каков вид зависимости потенциала Гиббса газов от давления?
51.Каков вид зависимости потенциала Гиббса конденсированных тел от давления?
52.Является ли вода стандартным веществом?
53.Какое состояние для воды является стандартным.
54.Стандартная абсолютная энтропия вещества обозначается алгебраическим символом S°. Что в нем означает верхний индекс « º »?
55.Какая из термодинамических функций используется чаще всего для хранения термодинамической информации в машиночитаемых базах данных? Почему?
56.Дайте определение понятию «компонент системы».
57.Дайте определение понятию «фаза».
58.В чем разница понятий «индивидуальное вещество» и «компонент системы»?
59.Дайте определение понятию «независимый компонент».
218
60.Сформулируйте теоретические признаки фазового равновесия в однокомпонентной системе.
61.Можно ли говорить о фазовых равновесиях в однокомпонентных системах?
62.Можно ли говорить о химических равновесиях в однокомпонентных системах?
63.Нарисуйте графическое отображение двухфазного равновесия в координатах {р,Т}.
64.Нарисуйте графическое отображение двухфазного равновесия в координатах {V,Т}.
65.Может ли фаза вещества существовать за пределами области ее термодинамической устойчивости? Приведите примеры.
66.При подводе тепла в теле происходит фазовый переход 1-го рода. Как при этом изменяется: энтальпия H; потенциал Гиббса G .
67.При подводе тепла в теле происходит фазовый переход 1-го рода. Как при этом изменяется: температура Т? энтропия S?
68.Выведите уравнение зависимости давления насыщенного пара от температуры.
69.Нарисуйте графическое отображение трехфазного равновесия в координатах {р,Т}.
70.Нарисуйте графическое отображение трехфазного равновесия в координатах {V,Т}.
71.Как зависит от давления температура плавления?
72.Напишите уравнение Клаузиуса – Клапейрона.
73.Как зависит температура кипения от давления?
74.Сформулируйте «правило фаз» Гиббса.
75.Что понимается под термодинамической степенью свободы?
76.Сформулируйте условия и критерии равновесия фаз для закрытых систем. Нарисуйте в пространстве Т, р, х геометрическое место равновесия двух и трех фаз.
77.Нарисуйте изменение теплоемкости с температурой для систем с фазовыми переходами первого и второго рода (например, для чистого железа с учетом полиморфных и магнитных превращений).
78.Дайте развернутое определение процесса фазового превращения.
79.Что является термодинамическим стимулом и движущей силой фазового превращения? Дайте различные варианты аналитического и графического представления движущей силы.
80.Какими соотношениями задается связь между скачками производных при фазовых превращениях первого и второго рода?
219
81.Дайте классификацию фазовых переходов по составу и структуре фаз, образующихся в результате превращения.
82.Сформулируйте условия и критерии стабильности образующихся в процессе фазового превращения фаз.
83.Как учесть упругие характеристики среды при расчете упругого вклада, учитывающего энергию деформации при образовании зародышей
новой фазы? Оцените величину εV с этих позиций.
84. Оцените относительную концентрацию равновесных зародышей критического размера на единицу объема исходной фазы для Т= 500К при переохлаждении Т= 50К, Нпр= 0,1 эВ, σs= 102 эрг/см2.
85.Получите выражение для критического размера модельной капли жидкой фазы, образующейся в паре.
86.Получите выражение для критического размера и критической энергии образования зародыша кубической формы при гомогенном зарождении.
87.Что вкладывается в понятие «раствор»?
88.Можно ли раствор считать фазой?
89.Что вкладывается в понятие «фаза переменного состава»?
90.Какая принципиально новая термодинамическая переменная появляется при описании растворов?
91.Что вкладывается в понятие «твердый раствор замещения»?
92.Что вкладывается в понятие «твердый раствор внедрения»?
93.Что вкладывается в понятие «твердый раствор вычитания»?
94.Как символом обозначаются мольные или атомные доли.
95.Что означает значок «%» в металлургии при описании состава растворов?
96.Какого типа будет раствор, в котором смешиваются практически идентичные вещества А и В, обладающие свойствами:
•одинаковы силовые характеристики взаимодействия (энергии взаи-
модействия E) как одноименных молекул между собой (UАА = UВВ), так и разнородных молекул (UАА = UВВ = UАВ);
•одинаковы размеры молекул: замена молекул А на молекулы В не вызывает изменения объема?
97. Что вкладывается в понятие «моль раствора»?
98. Что понимается под «парциальной молярной величиной».
99. Как алгебраически обозначается парциальная молярная величина?
100. Как связаны между собой парциальные и интегральные молярные величины?
220
101.Зависят ли химические потенциалы веществ от концентраций компонентов в идеальном растворе замещения?
102.Поясните, почему в идеальном растворе парциальные энтропии веществ зависят от концентрации.
103.Сформулируйте эмпирическое правило Юм-Розери.
104.Сколько мы имеем, в общем случае, неизвестных величин в математической модели бинарной смеси, описывающей равновесие двух фаз – двух идеальных растворов?
105.Сколько мы имеем, в общем случае, уравнений в математической модели бинарной смеси, описывающей равновесие двух фаз – двух идеальных растворов?
106.Что вкладывается в понятие "избыточные термодинамические функции"?
107.Дайте определение понятиям "активность" и "коэффициент активности".
108.Как изменяется давление пара над раствором при изменении концентраци?
109.Напишите уравнение Гиббса–Дюгема.
110.Дайте понятие о решеточной модели растворов.
111.В чем сущность квазихимического подхода в теории растворов?
112.В чем различие понятий дальнего и ближнего порядка?
113.Откуда появляется позиционная составляющая энтропии?
114.Сформулируйте критерии применимости моделей идеальных и совершенных растворов.
115.Какие избыточные функции совершенных растворов отличны от нуля и почему?
116.Какие избыточные функции совершенных растворов равны нулю
ипочему?
117.Какие избыточные функции регулярных растворов отличны от нуля и почему?
118.Какая избыточная функция регулярных растворов равна нулю и
почему?
119.Дайте определение, что такое параметр взаимодействия.
120.Какова взаимосвязь энтальпии смешения и параметра взаимодействия в модели регулярных растворов?
121.Как рассчитать коэффициент активности, если известен параметр взаимодействия?
122.Сформулируйте законы Рауля и Генри.
123.Какова зависимость активности от температуры и концентрации
вмодели регулярных растворов?
221
124.С чем связаны положительные и отрицательные отклонения от закона Рауля?
125.Сформулируйте правило Юм–Розери.
126.Опишите физическую модель субрегулярных растворов.
127.Опишите физическую модель квазирегулярных растворов.
128.Дайте математическую формулировку термодинамических законов равновесия в неидеальных системах.
129.В чем заключается сущность графической термодинамики Гиб-
бса?
130.Опишите математически концентрационную зависимость молярных потенциалов Гиббса для бинарных растворов.
131.Каков физический смысл общей касательной у кривых концентрационной зависимости молярных потенциалов Гиббса растворов, образующих разные фазы?
132.Нарисуйте диаграмму состояния неидеальной системы с неограниченной растворимостью и с положительным отклонением от закона Рауля.
133.Нарисуйте диаграмму состояния неидеальной системы с неограниченной растворимостью и с отрицательным отклонением от закона Рауля.
134.В чем физические причины распада твердых растворов? Какой знак для этого должен быть у параметра взаимодействия?
135.Нарисуйте график зависимость активности от концентрации при больших положительных отклонениях от идеальности.
136.Нарисуйте диаграмму состояния с куполом расслоения.
137.Какой тип распада раствора называется спинодальным? Нарисуй-
те график зависимости свободной энергии Gm(x) для твердого раствора, подверженного распаду. Покажите область спинодального распада.
138.Нарисуйте график зависимости свободной энергии Gm(x) для твердого раствора, подверженного распаду. Покажите область активационного распада.
139.Что такое критические зародыши.
140.Как рассчитать критическую температуру для спинодального и обычного распада.
141.Что такое «эвтектика»? Напишите эвтектические реакции.
142.Обоснуйте вид диаграммы состояния эвтектического типа при помощи кривых концентрационной зависимости изобарно-изотермичес- кого потенциала
143.Что такое «перитектика»? Напишите перитектические реакции.
222
144.Обоснуйте вид диаграммы состояния перитектического типа при помощи кривых концентрационной зависимости изобарно-изотермичес- кого потенциала.
145.Обоснуйте вид диаграммы состояния перитектического типа при помощи кривых концентрационной зависимости изобарно-изотермичес- кого потенциала.
146.Нарисуйте диаграмму состояния с монотектикой.
147.Нарисуйте диаграмму с синтектическим равновесием.
148.Привести типы Т–х диаграмм для систем, в которых возможна фиксация метастабильного состояния с последующими процессами распада пересыщенных твердых растворов и выделения фаз.
149.Привести примеры использования процессов искусственного и естественного старения в технологических целях.
150.Что такое «спинодаль» и «спинодальный» распад? Что означает «когерентная спинодаль»?
151.Указать и проанализировать последовательные стадии выделения.
152.В приближении регулярных растворов с параметром взаимодей-
ствия Ω(β) = 6934 кал/г ат (по Л. Кауфману) рассчитать критическую температуру купола расслоения для системы Zr–Nb и сравнить с экспериментальной Т–х диаграммой.
153.Решить предыдущую задачу в субрегулярном приближении с
Ω(β) = 4010 + х2.1430, кал/г-ат (по А.Г. Леснику, 1981). Построить асим-
метричный купол расслоения и оценить значение параметра асимметричности у.
154.Проанализировать особенности изотермического распада твердого раствора, состав которого не лежит в спинодальной области. Каков механизм этого типа распада?
155.Получить вид температурной зависимости растворимости метастабильной фазы.
156.Получить и проанализировать физический смысл уравнения Том- сона–Фрейндлиха.
157.Каким процессом лимитируется коагуляция выделений во время распада?
158.Дать общее определение и характеристику мартенситного превращения. Объяснить, почему это превращение относится к бездиффузионному типу?
159.Дать краткую характеристику кристаллографических особенностей мартенситного превращения.
223
