4.2.Метод термодинамических потенциалов
4.2.1.Равновесие в изолированных системах
Второй закон термодинамики гласит: в состоянии равновесия для данного значения энергии энтропия системы S имеет макси-
мальное значение. Именно это фундаментальное свойство энтропии лежит в основе всех расчетов численных значений термодинамических параметров статического равновесного состояния. Тем самым энтропия оказала революционное влияние на развитие термодинамики в целом, легла в основу теоретической термодинамики и стала таким же фундаментальным понятием науки, как энергия.
Промежуток времени, за который практически произойдет переход изолированной системы к термодинамическому равновесию, называют временем релаксации. Время релаксации тем больше, чем больше размер системы – ведь в ней должны завершиться процессы выравнивания давления, температуры и установиться равновесное распределение вещества.
Введем некоторые определения. Аддитивные переменные (объем, энергия, энтропия, масса и др.) в термодинамике называют экстенсивными. Они с очевидностью имеют смысл для любой, в том числе и неравновесной системы. Неаддитивные переменные, такие, как температура, давление, называют в термодинамике интенсивными. Они не имеют физического смысла применительно ко всей неравновесной системе – в ней существуют их градиенты, у
них нет единственного значения и можно говорить только о полях распределения температуры и давления.
Из условия отсутствия всех видов взаимодействия изолированной неравновесной системы с окружающей средой, получаем три необходимых условия сохранения трех независимых термодинамических экстенсивных переменных во время процесса ее релаксации
кравновесному состоянию:
1)постоянство ее объема V (с окружающей средой нет обмена работой);
2)постоянство внутренней энергии U (отсутствует теплообмен с окружающей средой);
36
3) постоянство количества вещества n (со средой отсутствует обмен массой).
Из сказанного выше следует, что для математического определения условий достижения состояния равновесия изолированной системой необходимо и достаточно представить энтропию как функцию только объема, внутренней энергии и числа молей, и найти в этих координатах условия, соответствующие ее глобальному максимуму.
Разобьем нашу большую систему на более мелкие части (подсистемы), но все еще остающиеся макроскопическими. Эти подсистемы могут быть физически определенными частями и являться, например, различными фазами или химическими соединениями. Но они могут быть и любым логическим разбиением по произвольному признаку.
Пусть выбранные подсистемы настолько меньше всей системы, что их время релаксации весьма мало, и в каждый момент времени их можно считать находящимися в состоянии термодинамического равновесия. В этом случае говорят о локальных равновесиях, и к любой подсистеме становятся применимы все понятия равновесной термодинамики, частности, понятия температуры и давления.
Для характеристики подсистем введем понятие о внутренних параметрах. Под ними будем подразумевать термодинамические величины Si, Ui, Vi, ni, Ti, рi …, определяющие состояние отдельных i-ых частей (внутренних подсистем), образующих данную систему.
Особенность введенных подсистем в том, что в процессе прихода всей замкнутой системы к равновесию они рассматриваются как неизолированные. Имеющаяся у них возможность осуществления между собой процессов обмена теплом, работой, массой приводит к изменению во времени τ значений их внутренних экстенсивных и интенсивных термодинамических переменных:
Ui = Ui(τ); Vi = Vi(τ); ni = ni(τ); Si = Si(τ); Ti = Ti(τ); рi = рi(τ).
Как аддитивная величина, вместе с ними изменяется (увеличивается) и энтропия системы в целом: S(τ) = ΣSi(τ). Но для других ее экстенсивных параметров, в силу изолированности системы, в каждый момент времени выполняются законы сохранения:
37
ΣUi(τ) = U; ΣVi(τ)= V; Σni(τ) = n. (4.19)
Если рассматривать только независимые переменные, что является необходимым и достаточным условием для полного описания системы, то высказанное утверждение имеет вид следующей математической записи:
S|U, V, n = ΣSi[Ui(τ), Vi(τ), ni(τ)] = f(τ).
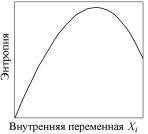
Конечные, равновесные значения всех внутренних параметров становятся такими, что энтропия всей изолированной системы S достигает своего глобального максимума. Интенсивные параметры подсистем приобретают определенные значения T, p – единственные для всех точек системы. Это позволяет дать еще одну формулировку второго начала термодинамики: в равновесном состоянии энтропия системы достигает своего глобального максимума (рис. 4.2).
Рис. 4.2. Качественная зависимость энтропии изолированной системы от внутренних экстенсивных переменных Хi (X = U, V, n)
Такая формулировка носит название принципа максимума энтропии. Тот факт, что энтропия имеет максимум при равновесии, оказалось ее важнейшим свойством, открывшим в термодинамике формально-математический, идеально общий путь для осуществления как теоретических исследований, так и выполнения практических вычислений по нахождению равновесного состояния.
Действительно, для получения условия максимума энтропии в обычной записи математического анализа, необходимо и достаточно вычислить частные производные энтропии всей системы S по независимым экстенсивным внутренним переменным Ui, Vi, ni и приравнять их нулю:
|
∂S |
|
|
|
|
∂S |
|
|
|
|
∂S |
|
|
|
|
|
|
= 0; |
|
|
|
= 0; |
|
|
= 0. |
(4.20) |
|||
∂U |
|
∂V |
|
∂n |
||||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
i |
|
|
i |
|
|
i |
|
|
||||
|
|
|
V , n |
|
|
|
|
U,n |
|
|
|
V ,U |
|
|
|
|
|
|
|
|
|
38 |
|
|
|
|
|
|
|
Добавив законы сохранения (4.19), получим систему математических уравнений, достаточную для формального описания и численного расчета параметров равновесного состояния, достигаемого в результате процесса релаксации в изолированной термодинамической системе. Другими словами, для математически формализованного поиска условий равновесия, если известны (заданы) конечные значения энергии U и объема V системы, то, исходя из принципа максимума энтропии, необходимо и достаточно:
1)записать явное выражение для энтропии конкретной изучаемой системы;
2)вычислить аналитически его первые частные производные
(4.20) по внутренним переменным Ui,Vi, ni и приравнять полученные выражения нулю;
3)записать выражения для всех законов сохранения (4.19) (массы, энергии, объема, заряда и т.п.);
4)решить полученную в пп. 2–3 систему уравнений относительно неизвестных Ui, Vi, ni;
5)используя уравнение состояния, рассчитать интенсивные величины – температуру и давление, установившиеся после прихода системы в равновесие;
6)по определению рассчитать энтальпию системы:
H = U + pV.
Единственным недостатком получающейся формально системы уравнений равновесия является ее сложность для аналитического решения, а в общем случае и для численного. На практике сложились определенные искусственные приемы облегчения нахождения таких решений. Одним из таких приемов является, например, составление уравнений химических реакций.
4.2.2. Термодинамические потенциалы
Выше подробно рассматривались свойства энтропии. Этой термодинамической функцией удобно пользоваться непосредственно для теоретического расчета равновесного состояния изолированных систем, в которых не идут физические или химические процессы взаимопревращения. Например, это – чисто механические
39
смеси индивидуальных веществ. В таких системах количества каждого из индивидуальных веществ, ее составляющих, не меняются ни от внешнего воздействия, ни во время релаксационных процессов. Установление равновесия здесь идет без воздействия внутренних источников тепла и вещества. Вся получаемая системой энергия в виде тепла и/или механической работы, идет только на ее простой нагрев. Энтропия системы является простой суммой абсолютных энтропий известных количеств индивидуальных веществ при новом значении внутренней энергии. Для нахождения новых условий равновесия (температуры, давления, объема) достаточно найти прирост энтропии системы, произошедший за счет выравнивания поля температур.
Более сложным случаем являются системы, в которых под влиянием внешнего начального воздействия происходят фазовые переходы и/или идут химические реакции. В этом случае, во время релаксации меняются количества индивидуальных веществ, каждое из которых имеет свое индивидуальное содержание энергии взаимодействия частиц из-за различия в атомных структурах. Поэтому происходят взаимные превращения тепловой энергии и энергии межатомного взаимодействия. Для процессов при постоянном давлении переход энергии межатомного взаимодействия в тепло определяется изменением значений энтальпий Н, а при постоянном объеме – внутренней энергии U. Ранее теплота фазовых переходов и химических реакций называлась скрытой теплотой, поскольку была неизвестна ее природа.
Естественно, что в общем случае при расчете конечной энтропии необходимо учитывать:
•внутренние источники тепла, действующие за счет превращения веществ;
•изменение количества индивидуальных веществ за счет обмена со средой.
Конечно, принцип максимума энтропии работает всегда. Но в обсуждаемых системах его прямое использование связано со значительными математическими трудностями. Система уравнений для поиска максимума энтропии с учетом сохранения энергии и массы даже в сравнительно простых случаях не имеет аналитиче-
40
ского решения. Численные методы решения и необходимые технические средства для их реализации появились сравнительно недавно, во второй половине ХХ века.
Для упрощения процедуры расчетов равновесий в системах с фазовыми превращениями Дж. В. Гиббс ввел новую термодинами-
ческую функцию G, учитывающую не только энтропию |
S, но и |
теплосодержание Н системы: |
|
G = H – TS. |
(4.21) |
В современной теоретической физике эта функция чаще всего называется потенциалом Гиббса. Название «потенциал» связано с тем, что функция G (а, как мы увидим ниже, и все другие термодинамические функции состояния) по своим свойствам относятся к особому классу математических потенциальных функций. Гиббс был первым, кто стал использовать в термодинамике математические свойства потенциальных функций (далее просто потенциалов).
Согласно определению, функция f(x, y, ... z) независимых (не связанных между собой) переменных x, y, … z является потенциальной, если ее полный дифференциал представим в виде
∂f df = ∂x y
|
|
∂f |
|
|
|
|
|
|
dx + |
|
|
,z... |
|
∂y x, z... |
|
|
∂f |
dz = 0, |
(4.22) |
dy +.... + |
|
||
|
∂z x, y... |
|
|
и равен нулю в каждой точке.
Поэтому интеграл от потенциальной функции по любому замкнутому контуру в координатах (x,y,..z) тоже равен нулю:
∫df = 0 .
Отсюда следует, что, если функция f(x, y, … z) описывает некоторое физическое свойство, то каждый раз при возвращении системы в исходное состояние (x0, y0, ... z0) его значение восстанавливается. Но это есть основное определение термодинамической функции состояния, т.е., все функции состояния являются потенциальными
вматематическом отношении.
Вобщем случае, как это и есть в термодинамике, независимые переменные x, y, … z в свою очередь могут являться функциями некоторых других величин u, v, … w. Очевидно, что значение функции f зависит и от этих неявных переменных. Более того, формально математически любые или все параметры x, y, … z
41
функции f можно заменять на любые из u, v, … w, лишь бы их число осталось неизменным и равным числу независимых переменных. Однозначность описания системы от этого не изменится. Однако вовсе не обязательно, что наша функция будет потенциальна относительно любого набора явных переменных из всех возможных их комбинаций.
Если значения одних переменных u, v, … w меняются произвольно (например, в ходе термодинамического процесса), но при этом значения других переменных x, y, … z остаются постоянными:
x(u,v, …w) = constx, y(u,v,…w) = consty, |
z(u,v,…w) = constz, |
то |
|
dx = dy = dz = 0. |
(4.23) |
В этом случае условие (4.21) выполняется, и тогда функция f является потенциальной относительно переменных x, y, … z (или, подругому, в координатах {x, y, … z}). В термодинамике такие пере-
менные носят название естественных переменных.
Для формального теоретического определения набора естественных переменных, относительно которого функция потенциальна, следует записать ее полный дифференциал и, как проверочное, использовать условие (4.23), которое является достаточным условием для доказательства потенциальности. Например, определим, относительно каких переменных будет потенциальна внутренняя энергия. Запишем приращение внутренней энергии dU в дифференциальной форме:
dU = δQ + δW = TdSe – pdV. |
(4.24) |
Отсюда видно, что если процесс идет при постоянном объеме (dV = 0) и без поступления тепла извне (δQ = 0, dSe = δQ/Т = 0), то выполняется условиие (4.23), а с ним и (4.21): dU = 0. Следовательно, внутренняя энергия является термодинамическим потенциалом относительно энтропии и объема.
Из (4.24) легко получить, что энтропия является потенциальной функцией относительно внутренней энергии и объема, поскольку:
dS = 1 |
T |
dU + P |
T |
dV . |
(4.25) |
|
|
|
|
|
|
||
Однако, несмотря на то, |
что энтропия – потенциальная функция, |
|||||
название «потенциал» к |
ней не применяется. В термодинамике |
|||||
|
|
|
42 |
|
|
|
термин «потенциал» используется только для функций, имеющих размерность энергии.
Взяв от формулы (4.11) – определения энтальпии H = U + pV
полный дифференциал: |
|
dH = d(U+pV) = dU +d(pV) = |
|
= (TdS – pdV)+(pdV + Vdp) = TdS + Vdp, |
(4.26) |
получаем, что теплосодержание есть термодинамический потенциал относительно энтропии и давления.
Последний результат важен в прикладном аспекте: из (4.26) видно, что если процесс изобарный и идет без теплообмена со средой, то сохраняется энтальпия системы (dH|S,р = 0). Это свойство энтальпии широко используется при теоретическом термодинамическом исследовании изобарных процессов.
Вычислив полный дифференциал (4.21): |
|
dG = d(H – TS) = (TdS + Vdp) – (TdS + SdT) = |
|
= Vdp – SdT, |
(4.27) |
видим, что для процессов, производимых с обменом теплом и работой со средой, но при постоянном давлении и температуре, потенциальной является функция Гиббса – потенциал Гиббса. Из (4.27) сразу следует, что если равновесный процесс идет при постоянных р,Т, то dG = 0.
Потенциал Гиббса часто называют изобарно-изотермическим потенциалом, поскольку он удобен для исследования процессов, проводимых при постоянных заданных (известных) значениях давления и температуры. Надо отметить, что изобарно-изотерми- ческие процессы наиболее широко используются в химической промышленности и металлургии. Отсюда очевидна большая значимость в прикладной термодинамике именно потенциала Гиббса.
Если температура и давление постоянны, то, дифференцируя
(4.27), с учетом (4.24) имеем:
dG = d(H – TS) = dH – TdS = [dU + d(pV)] – TdS = = [TdS + pdV] – TdS = pdV = –dW,
т.е. механическая работа W, совершаемая системой при постоянных p и Т, совпадает с потенциалом. Поэтому одной из трактовок физического смысла потенциала Гиббса является следующая формулировка: это та часть (H – TS) содержащейся в теле энергии (энтальпии H), которая может быть превращена в полезную работу W
43
впроцессе, осуществляемом при постоянных p и Т. В связи с этим
втехнической литературе изобарно-изотермический потенциал часто называют свободной энергией при постоянном давлении и температуре. Остающуюся часть (TS) энтальпии, которую принципиально нельзя превратить в работу, раньше называли связанной энергией; однако теперь это не принято.
Если процесс получения какого-либо полезного действия от системы проводится при постоянных объеме и температуре, то здесь потенциалом (изохорно-изотермическим) будет свободная энергия F в определении Гельмгольца:
F = U – TS. |
(4.28) |
Именно Гельмгольцу «свободная энергия» обязана своим названием.
Определим еще одну потенциальную функцию, нашедшую широкое применение на практике для проведения численных расчетов. Пусть система получила при постоянной температуре некоторое элементарное количество тепла δQ. Это изменило энтальпию и энтропию системы и дало приращение изобарно-изотермического
потенциала. Дифференцируя (4.21), имеем: |
|
dG = dH – TdS. |
(4.29) |
Перепишем (4.29) в виде: |
|
dG = – T (– dH/T + dS) . |
(4.30) |
По физическому смыслу членов в скобках (4.30) ясно, что dS – приращение абсолютной энтропии за счет разогрева системы, а – dH/T = dS* – приращение энтропии, связанное с поглощением тепла, пошедшем на изменение энтальпии за счет изменения состава. Следовательно, величина –H/T + S= –G/T может называться виртуальной энтропией системы. Именно ее максимум удобней всего отыскивать для определения равновесного состояния системы, в которой происходят не только механические процессы.
Реально величина –G/T получила название приведенный потенциал. Обозначается она символом Ф. Приведенный потенциал приобрел особое распространение для осуществления практических расчетов в связи с внедрением вычислительной техники в термодинамику. Связано это с прозрачностью его физического смысла и удобства формальной математической работы. М. Планк еще в 20-е
44
годы ХХ века в своих работах использовал эту функцию вместо потенциала Гиббса. Поэтому приведенный потенциал часто так же называют функцией Планка.
Введение Гиббсом понятия потенциалов явилось очень важным этапом в развитии термодинамики с точки зрения ее методологии. Действительно, используя математические свойства потенциальных функций, все термодинамические величины, характеризующие любую систему, могут быть получены как частные производные термодинамических функций. Например, из (4.24)–(4.26) сразу следуют важные соотношения, которые могут служить определениями температуры, давления и объема:
|
∂U |
|
∂H |
; |
T = |
|
= |
|
|
|
∂S V |
|
∂S P |
|
|
∂U |
|
1 |
∂S |
|
||
P = − |
|
= |
|
|
|
|
; |
T |
|
||||||
|
∂V S |
|
|
∂V U |
|||
|
∂H |
V = |
. |
|
∂P S |
или из (4.27) для энтропии и объема:
|
∂G |
; |
|
∂G |
(4.31) |
S = − |
|
V = |
. |
||
∂T p |
|
|
|
||
|
∂p |
|
|||
|
|
|
|
T |
|
Вывод подобных соотношений между первыми и вторыми частными производными функций и переменными, называемых соотношениями Максвелла, можно продолжить и показать, что, зная только одну любую потенциальную функцию и ее естественные переменные, можно получить все остальные характеристики системы. Поэтому потенциальные функции (они же – функции со-
стояния) часто называют характеристическими функциями.
4.2.3. Экстремальные свойства потенциалов
Для установления важнейшего свойства термодинамических потенциалов при прохождении неравновесных процессов вернемся к общим свойствам потенциальных функций. При произвольных вариациях переменных в окрестности точки (x, y, … z) вторым достаточным условием выполнения (4.22) является требование равенства нулю одновременно всех частных производных по аддитив-
ным (экстенсивным) естественным переменным:
45
|
∂f |
|
∂f |
|
|
∂f |
|
|
|
= 0 . |
|||||
|
|
= |
|
|
= ... = |
|
|
|
∂x y,z |
|
∂y x,z |
|
∂z x, y |
|
|
Частные производные функции равны нулю в двух случаях: когда функция постоянна или когда она имеет экстремум. Оба этих варианта в применении к характеристическим функциям и, в частности, к термодинамическим потенциалам, реализуются в термодинамике с конкретным физическим смыслом:
•постоянными значения термодинамических потенциалов, кроме очевидного случая самого состояния равновесия, остаются таковыми во время вынужденных равновесных процессов, осуществляемых при определенных условиях – своих для каждого потенциала. В частности, потенциал Гиббса остается постоянным при плавлении чистых веществ, имеющих четкую температуру плавления при заданном давлении. Для плавления к двухфазной системе непрерывно подводится тепло. Внутренняя энергия, энтальпия и энтропия при этом непрерывно увеличиваются за счет обмена со средой, но система остается равновесной; температура и давление всей системы остаются постоянными. А как следует из (4.26), потенциал Гиббса при этом не меняется;
•для неравновесных процессов в координатах естественных переменных потенциальная функция при достижении равновесия удовлетворяет другому условию равенства нулю ее первой производной – наличию у нее экстремума в данной точке. В термодинамической трактовке это описание пребывания системы в состоянии равновесия принимает форму теоремы: в состоянии равновесия функции состояния в координатах естественных переменных достигают своего глобального экстремального значения (миниму-
ма или максимума).
С максимумом энтропии мы уже столкнулись выше – обсуждаемое утверждение является ничем иным, как энтропийной формулировкой второго закона термодинамики. Сформулированная теорема позволяет расширить число прикладных расчетнотеоретических путей определения условий равновесия: кроме абсолютно универсального метода поиска глобального максимума энтропии, можно решать более частную, но и более простую задачу на поиск экстремума какой-либо другой функции состояния – тер-
46
модинамического потенциала. Но это следует делать в соответствующих координатах, в ее естественных переменных, относительно которых данная функция потенциальна.
Для выяснения экстремального свойства потенциала Гиббса рассмотрим изобарную систему, получившую извне некоторое элементарное количество тепла δQe , что вызвало в ней необратимые процессы – фазовые превращения, химические реакции – а с ними и производство энтропии. Одна из формулировок второго закона термодинамики отражает этот факт в виде уравнения: dS >
δQe /T (см. (4.21)), которое запишем следующим образом: |
|
δQe – TdS < 0. |
(4.32) |
Поскольку процесс изобарный, то количество поступившего тепла δQ равно изменению энтальпии системы dH. Возникающие при этом необратимые процессы в силу закона сохранения энергии изменения энтальпии системы не производят. Поэтому δQe = dH, и, с
учетом постоянства температуры, из (4.32) имеем: |
|
δQe – TdS = dH – TdS = d(H – TS) = dG < 0. |
(4.32а) |
Таким образом, необратимые процессы, осуществляемые при постоянных температуре и давлении, идут с уменьшением энер-
гии Гиббса. Поскольку при достижении равновесного состояния в системе уже ничего не меняется, то с этого момента dG/dτ становится равным нулю. Следовательно, в равновесии потенциал Гиб-
бса всей системы достигает своего минимального значения при заданных значениях р и Т. Аналогично можно показать минимальность свободной энергии Гельмгольца при заданных объеме и температуре и минимальность энтальпии при постоянных энтропии и давлении.
4.2.4. Химический потенциал
Выше в основном рассматривались системы с постоянным количеством веществ в них. Однако системы с переменным числом частиц – количеством веществ в разных химических формах или агрегатных состояниях – имеют важнейшее значение на практике и являются основными объектами изучения в химической термодинамике. Имеется так же целый класс открытых систем, обмени-
47
вающихся веществом с окружающей средой. Методологию теоретического изучения систем с изменяющимся количеством вещества заложил Дж. Гиббс. Собственно говоря, для рассмотрения именно таких систем и потребовалось введение термодинамических потенциалов.
Запишем первый закон термодинамики по Клаузиусу:
dU = δQe + δW = TdSe – pdV, (4.33)
где δQe и dSe – элементарное количество тепла и соответвующее ему изменение энтропии, полученные извне.
В выражении (4.33) учтены только тепловые и механические явления. Но, поскольку любая система состоит из каких-то веществ, то изменение их количеств ni так же приводит к изменению ее термодинамических характеристик. Гиббс предложил следующую форму записи учета этого изменения, которая для открытых систем имеет вид:
dU = TdSe – pdV + Σμjdnej, |
(4.34) |
где через dnej обозначены количества веществ, поступивших извне, а через μj – коэффициент пропорциональности между количеством вещества и сообщаемой им энергией. Этот коэффициент назван Гиббсом химическим потенциалом, поскольку формула (4.34) в отличие от (4.33) становится применима к системам с физикохимическими процессами. Она является основой для большой области науки, называемой химической термодинамикой. Сам Гиббс назвал соотношение (4.34) фундаментальным уравнением термо-
динамики.
В открытых системах, допускающих обмен веществом с окружающей средой, изменения dnj могут происходить под влиянием внешнего воздействия (dnej), что вносит вклад в изменение энергии системы dU. Как в открытых, так и в закрытых системах изменения dnj могут происходить (dnij) так же за счет взаимопревращений веществ – химических реакций и/или фазовых переходов. Но такие чисто внутренние физико-химические превращения, в силу первого закона термодинамики, вклада в изменение энергии, в том числе и
внутренней, не дают: |
|
dUi = Σμjdnij = 0. |
(4.35) |
48 |
|
Смысл выражения (4.35) в том, что оно накладывает определенные ограничения на возможные изменения количеств веществ во время химических реакций: количества одних должны убывать, других – возрастать, причем так, чтобы выполнялось условие равенства нулю суммы в (4.35).
Выражение (4.35) отражает самопроизвольное стремление системы к переходу в равновесное состояние; оно же является дифференциальной формой описания самого химического равновесия.
Для получения условия равновесия в более практичном виде воспользуемся понятием химической реакции. Химические реакции в общем случае записываются как символические равенства, которые имеют вид (если перенести все члены в одну сторону):
ΣνjAj = 0, (4.36)
где Аj – химические символы реагирующих веществ, а коэффициенты νj – положительные или отрицательные, обычно целые, числа.
Например, уравнение реакции в привычной записи:
2Н2 + О2 = 2Н2О
в формализованном виде будет иметь вид:
–2Н2 – О2 + 2Н2О = 0,
ибо согласно правилу, принятому в термодинамике, стехиометрические коэффициенты у исходных веществ считаются отрицательными (количества веществ убывают), у продуктов реакции – положительными (вещества появляются). В нашем примере:
νH2 = –2, νO2 = –1, νH2O = +2.
В силу закона сохранения материи, изменения dnj чисел молей веществ nj во время химической реакции связаны друг с другом уравнением этой реакции. Например, если n1 изменится на ν1 молей, то каждое из остальных обязано измениться на νj. Другими словами, условие стехиометрии реакции можно записать как
нормировочное соотношение: |
|
|
|
|
|
|
|
||||||
|
dn |
|
dn j |
|
|
|
|
dn |
|
||||
|
|
1 |
= |
|
|
|
или dn |
j |
=ν |
j |
1 |
. |
(4.37) |
|
ν |
1 |
|
ν |
j |
|
|
ν |
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
|||
Подставляя (4.37) в (4.35) и сокращая на общий член dn1/ν1, имеем:
49
Σμjdnj = Σμ |
ν |
|
dn1 |
= |
dn1 |
Σμ |
ν |
|
= Σμ |
ν |
|
= 0. |
(4.38) |
|
j ν |
ν |
j |
j |
|||||||||||
j |
|
|
j |
|
j |
|
|
|
||||||
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|||
Это и есть искомое условие химического равновесия. Для того чтобы записать его, надо в уравнении химической реакции символы веществ Аj формально заменить на соответствующие химические потенциалы μj.
В случаях, когда в смеси возможны несколько различных реакций, условием равновесия будет являться система нескольких уравнений типа (4.38). В случае фазового равновесия одного вещества, когда α-фаза превращается в β-фазу, условие равновесия будет особенно простым. Записав фазовый переход как химическую реакцию:
А(α) = А(β) |
или |
А(β) |
– А(α) = 0 |
|
имеем: |
|
|
|
|
μ(β) – μ(α) = 0 |
или |
μ(β) |
= μ(α). |
(4.39) |
Для проведения практических расчетов фазовых и химических равновесий по уравнениям (4.38) или (4.39) необходимо выяснить физический смысл химического потенциала и определить простейший путь его численного расчета. Поэтому, прежде всего, установим связь химического потенциала со всеми термодинамическими потенциалами.
Проведем некоторые преобразования выражения (4.34), связывающее изменение внутренней энергии dU с поступившими извне
теплом δQe = TdSe , работой δW = – pdV и массой Σμjdnej. Суммируя
(4.34) и (4.35), имеем:
dU = TdSe – pdV + Σμj(dnej+ dnij) = TdSe – pdV + Σμjdnj, (4.40)
где dnj – общее изменение числа молей веществ в результате внешнего воздействия и релаксационных химических процессов. Поскольку релаксационные процессы в системе всегда необратимы, то согласно Пригожину в ней будет производиться энтропия: dSi > 0. Тогда (4.40) можно переписать в виде:
dU = T dSe – pdV + Σμjdnj ≤ T (dSe + dSi) – pdV+ Σμjdnj
или |
|
dU ≤ TdS – pdV + Σμjdnj, |
(4.41) |
где dS – полное изменение энтропии системы под влиянием внешнего воздействия. Уравнение (4.41) является объединением 1-го и
50
2-го законов термодинамики. Знак равенства в нем относится к равновесным процессам или, в пределе, к состоянию равновесия. Знак неравенства «<« справедлив для неравновесных процессов. Следовательно, внутренняя энергия системы убывает во время неравновесного релаксационного процесса, достигая своего глобального минимума при заданных (известных) значениях энтропии и объема. Что и было впервые строго показано Гиббсом.
Получим теперь для химических потенциалов более общие выражения – фундаментальные уравнения, как назвал их Гиббс. Воспользуемся для этого несложными искусственными преобразованиями уравнения (4.41), которые, в принципе, являются преобразованиями Лежандра. Прибавим к левой и правой части (4.41) одно и
то же слагаемое d(pV): |
|
dU + d(pV) ≤ TdS – pdV+ d(pV)+ Σμjdnj |
|
и проведем элементарные преобразования: |
|
d(U + pV) ≤ TdS – pdV+ pdV+ Vdp+ Σμjdnj |
|
или в силу определения энтальпии (см. п. 4.1.6): |
|
dH ≤ TdS + Vdp+ Σμjdnj . |
(4.42) |
Отсюда видно, что энтальпия системы убывает во время неравновесного процесса, достигая своего глобального минимума при заданных (известных) значениях энтропии и давления.
Вычтем теперь из левой и правой части (4.41) величину d(TS): dU – d(TS) ≤ TdS – d(TS)– pdV + Σμjdnj
и, проведя преобразования: |
|
d(U –TS) ≤ TdS – TdS – SdT – pdV + Σμjdnj , |
|
получаем |
|
dF ≤ – SdT – pdV + Σμjdnj . |
(4.43) |
Выражение (4.43) является фундаментальным уравнением относительно свободной энергии Гельмгольца, которая достигает глобального минимума в неравновесных изохорно-изотермических процессах.
Для получения фундаментального уравнения для потенциала Гиббса достаточно вычесть d(TS) из левой и правой части (4.42). В
результате получим соотношение: |
|
dG ≤ – SdT + Vdp+ Σμjdnj , |
(4.44) |
51
из которого видно, что энергия Гиббса системы в целом достигает глобального минимума в неравновесных изобарно-изотермических процессах; в равновесных она остается постоянной.
При выводе фундаментальных уравнений (4.41)–(4.44) все преобразования совершенно не затрагивали член Σμjdnj. Следовательно, во всех этих выражениях для полных дифференциалов различных функций стоят одни и те же численные значения химических потенциалов μj. Но они, естественно, выражаются через частные производные разных величин при различных фиксированных переменных, естественных для данного потенциала:
|
|
|
|
∂G |
|||
μ |
|
= |
|
|
|
|
|
|
∂n |
|
|||||
|
j |
|
|
|
|
||
|
|
|
|
|
|
j T , p,n |
|
|
|
|
|
|
|
|
i≠ j |
|
|
∂H |
|
|
|||
= |
|
|
|
|
|
|
|
∂n |
|
|
|
||||
|
|
|
|
|
|
||
|
|
|
j S , p,n |
||||
|
|
|
|
|
|
|
i≠ j |
|
∂F |
|
|
|
||||
= |
|
|
|
|
|
|
= |
|
|
|
|
|
|
||||
∂n |
|
|
|
|
||||
|
|
|
j T ,V ,n |
|
||||
|
|
|
|
|
|
|
i≠ j |
(4.45) |
|
|
∂U |
||||||
|
|
|||||||
= |
|
|
|
|
|
|
. |
|
|
∂n |
|
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
j S ,V ,n |
|
|||
|
|
|
|
|
|
|
i≠ j |
|
Выпишем выражения, которые являются определениями важ-
нейших термодинамических функций: |
|
|
|
энтальпия: |
H(S,p) |
= U + p·V; |
|
энергия Гельмгольца: |
F(V,T) |
= U – T·S; |
(4.46) |
потенциал Гиббса: |
G(T,p) |
= H – T·S. |
|
Поскольку в состоянии термодинамического равновесия давление р и температура T постоянны внутри всей системы, то из аддитивности (экстенсивности) внутренней энергии U, объема V, энтропии S следует и аддитивность (экстенсивность) величин H, G, F. По определению, аддитивная величина ϕ(x) есть такая, для которой выполняется условие: ϕ(n·x) = n·ϕ(x).
По физическому смыслу аддитивность величины означает, что изменение количества вещества (количества его молей) в некоторое число n раз приводит к изменению этой величины во столько же раз, т.е. число молей является как бы множителем перед некоторой функцией, которая описывает термодинамическое свойство,
приходящееся на один моль: |
|
U(S,V,n) = n·u(S/n, V/n); |
(4.47) |
H(S, p, n) = n·h(S/n, p); |
(4.48) |
52 |
|
F(V, T, n) = n·f(V/n, T); |
(4.49) |
G(T, p, n) = n·g(T, p). |
(4.50) |
Для простоты рассуждений выражения (4.47)–(4.50) записаны для случая, когда тело состоит из частиц одного сорта.
Выполним теперь дифференцирование уравнений (4.47)–(4.50) по количеству n вещества, что даст различные формулы для определения химического потенциала:
μ(S,V ,n) = |
∂U |
|
S |
|
|
V |
|
|
|
∂u |
|
∂u |
|
|||||||||||
∂n |
= u |
|
|
|
, |
|
|
|
+ n |
|
|
|
|
+ |
|
|
ln n; |
|||||||
|
|
|
n |
|
|
|
|
|
||||||||||||||||
|
|
n |
|
|
|
|
|
∂S |
|
∂V |
|
|||||||||||||
|
∂H |
|
S |
|
|
|
|
|
∂h |
|
|
|
|
|
|
|||||||||
μ(S, p,n) = |
|
= h |
|
|
|
, p |
+ n |
|
|
|
|
ln n; |
|
|||||||||||
∂n |
|
|
∂S |
|
||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
(4.51) |
|||||||||||
|
∂F |
|
V |
|
|
|
|
|
|
|
∂f |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
μ(V ,T ,n) = |
|
= |
f |
|
|
,T |
|
+ n |
|
|
|
|
|
ln n; |
|
|||||||||
∂n |
|
|
|
|
∂V |
|
|
|||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
μ(T , p,n) = |
∂G |
= g(T , p). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∂n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как видно, только частная производная по количеству вещества от потенциала Гиббса, одна из всех производных от термодинамических функций состояния, обладает особым свойством: она не за-
висит от количества вещества, т.е., эта частная производная сов-
падает с полной. Тогда имеем:
∂G |
dG |
(4.52) |
∂n |
= g(p,T)= μ(р,Т) = . |
|
dn |
|
Из (4.51) и (4.52) сразу следует выражение:
G = n·μ(р,Т), (4.53)
раскрывающее физический смысл химического потенциала: это есть потенциал Гиббса, отнесенный к единице массы вещества.
Значение величины, отнесенное к одному молю вещества, называется молярной, например: молярная теплоемкость, молярный потенциал Гиббса и т.д. В силу сказанного, молярный потенциал Гиббса в химической термодинамике отождествляют с понятием хи-
мического потенциала. Молярные величины других термодинамических функций U, H, F химическими потенциалами не являются,
поскольку их частные и полные производные не совпадают (см. выражения (4.51)).
53
4.2.5. Явные условия термодинамического равновесия
Выше подробно обсуждались глобальные условия определения достижения системой состояния термодинамического равновесия: экстремальность в равновесии или постоянство во время процесса той или иной термодинамической характеристической (потенциальной) функции всей системы. Такие условия пригодны и широко используются в теоретических исследованиях, а так же для численных расчетов равновесного состояния. Однако они все же носят скорее теоретический, чем практический характер. Поэтому найдем дополнительные, более простые, явные условия термодинамического равновесия, выражаемые через наиболее легко экспериментально измеряемые или рассчитываемые теоретически термодинамические параметры.
Прежде всего, заметим, что такие параметры должны быть интенсивными (не аддитивными) термодинамическими величинами,
так как должны характеризовать всю систему в целом и иметь физический смысл только в состоянии равновесия. Экстенсивные
(аддитивные) величины имеют свои значения для всей системы и в неравновесных условиях.
Таких величин должно быть ровно три, поскольку независимых термодинамических переменных, через которые с помощью характеристических функций можно рассчитать все остальные параметры равновесного состояния, именно три. Выполнение в каждой точке условия постоянства во времени и пространстве значений трех (и только трех) интенсивных термодинамических величин, и
служит доказательством достижения состояние полного термодинамического равновесия. Две из необходимых интенсивных величин уже известны из феноменологии:
•давление p, постоянство которого во всех точках системы означает установление механического равновесия. Это условие означает отсутствие конвекции – макроскопического взаимного движения отдельных частей системы;
•температура Т, постоянство которой во всех точках системы означает установление теплового равновесия. Как говорилось выше, это условие называется нулевым законом термодинамики. Оно
54
означает отсутствие в системе направленных макроскопических тепловых потоков.
Двух термомеханических условий равновесия достаточно для технической термодинамики. В химической термодинамике необходимо принимать во внимание третье условие равновесия, которое должно отражать отсутствие массовых потоков, макроскопических по проявлениям, но осуществляющихся на молекулярном уровне, а именно:
•пространственных, происходящих по механизму диффузии;
•временных, за счет химических реакций и фазовых превращений.
Поэтому надо найти интенсивную величину, связанную с коли-
чеством вещества и остающуюся постоянной во всех точках системы при равновесии. Такой величиной является химический потен-
циал μ, или, что то же самое, парциальный молярный потенциал Гиббса. Докажем это строго математически.
Два обсуждаемых условия равновесия были установлены экспериментально, причем еще до создания термодинамики как строгой науки. Владея теперь аппаратом теоретической термодинамики, созданного Гиббсом на основе свойств потенциальных функций, эти положения легко обосновать теоретически. Покажем это на примере температуры.
Рассмотрим случай неравновесных процессов в изолированной неравновесной системе. Из изолированности системы, т.е. из отсутствия взаимодействия с окружающей средой, имеем следующие условия прохождения такого процесса:
•постоянство объема V (не совершается механическая работа);
•постоянство внутренней энергии U (отсутствует теплообмен с окружающей средой);
•постоянство количества вещества n (отсутствует массопере-
нос).
В то же время в системе могут самопроизвольно проходить, на-
пример, фазовые превращения. Фазовые превращения сопровождаются перераспределением количества числа частиц между фазами, обладающими различными физическими свойствами. При условии постоянства объема это приводит к изменению давления р в системе, выделению/поглощению тепла внутри системы, к измене-
55
нию энтальпии Н. И, конечно, изменяется (точнее, увеличивается), энтропия S системы в целом, по достижению максимума которой наступает равновесное состояние.
Из сказанного следует, что для математического определения условий достижения изолированной системой состояния равновесия удобно представить энтропию как функцию внутренней энергии, объема и числа молей. В этих координатах дифференциал энтропии:
dS = |
1 |
dU + |
1 |
PdV + |
1 |
μdn |
(4.54) |
|
T |
T |
|||||
|
T |
|
|
|
|||
является полным, и именно в них следует искать условия равенства нулю соответствующих частных производных.
Выполним необходимые действия. Пусть наша изолированная система состоит всего из двух тел. Энтропия системы – функция аддитивная:
S = S1(U1,V1, n1) + S2(U2,V2, n2).
Из шести переменных U1, V1, n1, U2, V2, n2 в силу изолированности системы независимыми являются только три, поскольку:
U = U1 +U2 = constU,
V = V1 +V2 = constV, (4.55) n = n1 +n2 = constn.
Выберем в качестве такой независимой переменной, например, U1. Тогда условие максимума энтропии можно записать в виде:
∂S |
|
|
|
|
|
∂S1 |
|
|
|
∂S2 |
|
|
|
|
|
∂S1 |
|
|
|||||||
|
|
|
|
= |
|
|
|
+ |
|
|
|
= |
|
|
+ |
||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
∂U1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
∂U1 |
|
|
∂U1 |
|
|
|
|
∂U1 |
|
|||||||||||
|
|
|
V ,n |
|
|
|
|
|
|
|
V ,n |
|
|
|
|
V ,n |
|
|
|
V ,n |
|
||||
|
∂S ∂U |
|
|
|
|
|
|
|
∂S |
|
|
|
|
|
|
∂S |
2 |
|
|
|
|
||||
|
|
|
|
|
|
2 |
|
= |
|
1 |
|
|
− |
|
|
|
= 0, |
|
|||||||
+ |
|
|
|
|
|
|
∂U1 |
|
|
∂U2 |
|
|
|||||||||||||
|
∂U2 ∂U1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
V ,n |
|
|
|
|
V ,n |
|
|
|
|
V ,n |
|
|||||||
отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂S1 |
|
|
|
|
|
|
∂S2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
(4.56) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂U2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
∂U1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
V ,n |
|
|
|
|
|
V ,n |
|
|
|
|
|
||
Этот вывод легко обобщается на случай любого числа тел, находящихся в равновесии друг с другом. Таким образом, если сис-
56
тема находится в состоянии термодинамического равновесия, то производная энтропии по энергии для каждой из ее частей одинакова, т.е. постоянна по всей системе. Величина, обратная производной энтропии по энергии, как следует из (4.54) или (4.25), явля-
ется ничем иным, как эмпирической абсолютной температурой
|
∂U |
(4.57) |
T = |
. |
|
|
∂S V ,n |
|
Следовательно, условие (4.56) эквивалентно феноменологическому утверждению, что температуры тел, находящихся в равнове-
сии, равны: T1 = T2.
Из (4.57) можно получить связь между определением энтропии, эмпирической температурой и энергией:
dS = |
dU |
. |
(4.58) |
|
|||
|
T |
|
|
Поскольку внешняя работа не совершалась, dU может быть только вариацией (элементарным количеством) тепла: dU = δQ, и тогда (4.58) превращается в классическое определение энтропии как приведенной теплоты Kлаузиуса:
dS = δTQ .
Аналогично из максимума энтропии можно получить и второе эмпирическое условие достижения равновесия – постоянство давления по всей системе. Третье явное необходимое условие равновесия относительно распределения вещества в закрытой системе найдем из экстремума изобарно-изотермического потенциала Гиббса G как наиболее удобной характеристической функции при заданных давлении и температуре.
Рассмотрим некоторое тело, содержащее n молей какого-либо вещества. Как и ранее, разделим тело на две части (например, фазы), содержащие соответственно n1 и n2 молей этого вещества, но потребуем теперь условия минимума потенциала Гиббса по отношению к распределению вещества между подсистемами, при условии постоянства температуры и давления. С учетом закона сохранения материи n = n1 + n2, имеем:
57
|
∂G(T , p, n) |
|
|
|
|
|
∂n1 |
|
|
T , p |
= |
∂G1 |
+ |
∂G2 ∂n2 |
= |
∂G1 |
− |
∂G2 |
=0. (4.59) |
|
|
∂n |
|
∂n |
∂n |
|
∂n |
|
∂n |
|
|
1 |
|
2 |
1 |
|
1 |
|
2 |
|
Согласно (4.51), производная от потенциала Гиббса подсистемы по количеству вещества в ней есть его химический потенциал: уравнение (4.59) означает, что при равновесии макроскопической системы в каждой ее точке r должно выполняться условие постоянства химического потенциала:
|
∂G |
= |
μ(p,T)= const(r), |
(4.60) |
|
|
|||
|
∂n T , p |
|
|
|
которое и есть искомое третье явное условие достижения состояния полного термодинамического равновесия.
Если веществ (сортов молекул) в системе много, то условие типа (4.60) должно выполняться для каждого из них:
|
∂G |
|
|
|
||
|
|
= μi (p,T) = consti(r). |
(4.61) |
|||
|
||||||
|
∂n |
|
|
|
|
|
|
|
i T , p,n j≠i |
|
|
||
Выполнение условий (4.61) указывает на то, что в системе наступило массовое равновесие – в ней больше не идут химические реакции и фазовые превращения одного вещества в другое, не идет изменение концентраций веществ за счет диффузии. По-другому: выполнение этих условий означает отсутствие макроскопических потоков вещества во времени и пространстве, которые могли бы происходить за счет процессов на микроуровне.
Но массовое равновесие здесь, конечно, динамическое: микроскопические потоки массы (обмен частицами между фазами и химическими формами на молекулярном и атомном уровнях) идет непрерывно. Можно утверждать, что за достаточно большое время любой атом побывает не только в любой точке пространства системы, но и во всех химических сочетаниях (соединениях) с другими атомами. С помощью этих обменных процессов на микроуровне собственно и поддерживается состояние равновесия, при котором массовые количества различных фаз и химических форм молекул остаются постоянными в каждый момент времени. Название «химический потенциал» и введено Гиббсом в связи с тем, что именно
58