Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северо-Западный институт управления РАНХиГС (СЗАГС)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ВКР-2010(Поляков).pdf

Скачиваний:

971

Добавлен:

15.05.2015

Размер:

4.39 Mб

Скачать

☆

<<< < Предыдущая 28 29 30 31 32 33 34 35 36 37 38 3940 / 5440 41 42 43 44 45 46 47 48 49 50 51 52 > Следующая >>>

232

ции: r01 = - 0,811; r02 = - 0,586; r12 = 0,502. В строке, обозначенной , приведены оценки средних квадратических откло-

нений: y = 9,19; x1 = 89,16; x2 = 6,36.

Составим систему нормальных уравнений в стандартизированном виде:

1 0,502 2 0,811,0,502 1 2 0,586.

Для решения системы уравнений по методу Крамера вычислим определители:

					1	0,502			1 0,252 0,748,
				0,502		1
x		0,811			0,502		0,811 0,294 0,517,
x		0,811			0,502		0,811 0,294 0,517,
1		- 0,586			1

	x				0,811			0,589 0,407 0,182.
			1		0,811			0,589 0,407 0,182.
		2	0,502		- 0,589
		2

Следовательно, 1 = -0,517 / 0,748 = - 0,69; 2 = -0,182 / 0,748 = - 0,24.

Переходя от стандартизированного вида к натурально-

му, получим:
		а1 = 1 у / 1 = - 0,69 . 9,19 / 89,16 = - 0,071;
		а2 = 2 у / 2 = - 0,24 . 9,19 / 6,36 = - 0,347;
a	0	y a x		a	2	x	2	= 73,0–(-0,071).418,6–(- 0,347). 25,6 = 111,6.
	0	1	1		2		2
		Следовательно, уравнение множественной регрессии в
натуральном масштабе имеет вид-
				y = 111,6 – 0,071х1 – 0,347х2.					(6.185)
		По величине коэффициентов а1 и а2 можно							судить,

насколько изменится зависимая переменная, если соответствующая независимая переменная изменится на единицу, при условии, что остальные переменные сохраняют постоянное значение.

6.8.5 Оценка тесноты связи и значимости коэффициентов регрессии

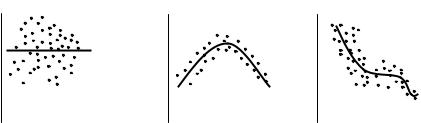
При изучении корреляционных зависимостей возникает необходимость в измерении (оценке) тесноты связи. Рассмотрим два корреляционных поля а и б (рисунок 6.50).

Пусть линии регрессии у по х в обоих полях расположены примерно одинаково, однако точки поля а расположены гораздо ближе к линии регрессии, чем точки поля б. Если бы функция у полностью определялся аргументом х, то все точки лежали бы на

Y |x

233

линии регрессии. Чем сильнее влияние прочих факторов, тем дальше точки отстоят от линии регрессии. Очевидно, что в случае а прочие факторы меньше влияют на аргумент х, чем в случае б , и зависимость между у и х является более тесной.

x		x
а) сильная связь		б) слабая связь

Рисунок 6.50 - Линейная регрессия при различной тесноте связи

За основу показателя тесноты связи берется общий показатель изменчивости – полная дисперсия Y2 . Полной дисперсией Y2 называют дисперсию Y относительно условного генерального среднего μY.

Дисперсию Y2 можно разложить на две составляющие,

одна из которых характеризует влияние данного фактора Х на Y, вторая – влияние прочих факторов. Очевидно, чем меньше влияние прочих факторов, тем сильнее связь.

Представим 2	в виде
Y		M Y y 2 M y Y 2
Y2 Y2\|x	Y2\|x	M Y y 2 M y Y 2		(6.186)
Первое слагаемое 2			- это дисперсия переменной Y от-
	Y \|x

носительно теоретической линии регрессии y ; она измеряет влияние так называемых прочих факторов на Y.

Второе слагаемое Y2|x - это дисперсия теоретической

линии регрессии относительно условной генеральной средней; она измеряет влияние фактора X на Y.

Поскольку дисперсия оценивает влияние фактора X

на результативный признак Y, то ее можно использовать для оценки тесноты связи между X и Y. Тесноту связи удобно оце-

нивать в долях (единицах) общей дисперсии						2	, т.е. рассмат-
						Y
ривать отношение	M y		2
T2	M y	Y	2	Y2\|x	,		(6.187)
		Y
	2			2
	2			2
	Y			Y

234

которое называется теоретическим корреляционным отношением.

Если разделить обе части равенства (6.187) на Y2 , то

возможно получить другое выражение для теоретического корреляционного отношения

						2
			T2 1			Y \|x		.	(6.188)
			T2 1					.	(6.188)
							2
						Y
Поскольку	2	2	, т.к.	2			является составной ча-
	Y \|x	Y			Y\|x

стью Y2 , то из равенства (6.188) следует, что значение T2 находится всегда между нулем и единицей.

Из равенства (6.188) следует, что T2 0 тогда и только тогда, когда y Y const , т.е. линия регрессии есть гори-

зонтальная прямая, проходящая через центр распределения. В этом случае можно утверждать, что переменная Y не коррелирована с X (рисунок 6.51, а).

Из равенства (6.188) следует, что T2 1 только тогда, когда Y|x2 0 , т.е. отсутствует влияние прочих факторов и все распределение сконцентрировано на линии регрессии y . В этом случае связь между Y и X является функциональной. Примерный вид линии регрессии, когда T2 1, представлен на рисунке 6.51, б.

В общем случае, когда 0 T2 1, линия регрессии представлена на рисунке 6.51, в.

T2 0		2	1
y	y	T
y	y
y			y	y

0 T2 1

x		x		x
а)		б)		в)

Рисунок 6.51 - Свойства теоретического корреляционного отношения

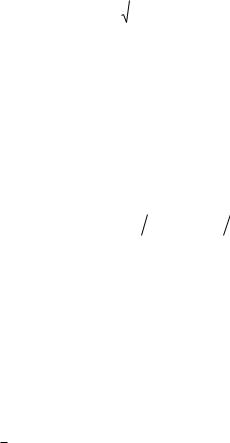
235

Некоррелированность не следует смешивать с независимостью: если T2 0 , то переменная Y может зависеть от X ,

но так, что центры условных распределений не меняются, а изменяются условные дисперсии.

В исследованиях часто используется величина, которая также называется теоретическим корреляционным отношением,

	T		2		Y \|x	/	Y	,	(6.189)
	T		TY\|x		Y \|x		Y

и также считается, что она не может быть отрицательной. Значения этой величины могут находиться в пределах от нуля до единицы.

Перед тем как начать исследование формы связи, в случае, если вид зависимости еще не установлен, а коэффициенты регрессии не вычислены, часто бывает необходимо убедиться в наличии какой бы то ни было связи между переменными. Может оказаться, что связь несущественна и вычисление коэффициентов регрессии неоправданно. В этом случае вычисляется эмпирическое корреляционное отношение.

Подобно теоретическому эмпирическое корреляционное отношение можно записать в виде

2	2	s2	1 s2	s2	,	(6.190)

	y\|x	y	y\|x	y

где y2|x - оценка межгрупповой дисперсии;

s y2|x - оценка дисперсии зависимой переменной Y относительно эмпирической линии регрессии;

s y2 - оценка полной дисперсии зависимой переменной Y.

Оценка дисперсии зависимой переменной определяется по формуле

sy2	1	y yi x 2	1	yi x		2 , (6.191)
					y
	n		k

где y - измеренное значение зависимой переменной; yi(x) – среднее значение в данном интервале;

y - среднее всей совокупности;

k - количество интервалов; n - общее число измерений.

Из сравнения формул (6.186) и (6.191) следует, что различие между теоретическим и эмпирическим корреляционным отношением заключается в том, что при расчете теоретического корреляционного отношения необходимо знать уравнение регрессии, при расчете эмпирического корреляционного отноше-

236

ния о форме связи не делается никаких предположений и расчет ведется с использованием эмпирической линии регрессии.

По данным, приведенным в таблице 6.29, для нелинейной регрессии (типа гипербола) вычислить теоретическое и эмпирическое корреляционное отношение.

Для расчета теоретического корреляционного отношения представим Y2 и Y|x2 в следующем виде:

y 2 my

ymy

;

(6.192)

Y|x2

2 mx ;

(6.193)

ymy / my ,

(6.194)

где y - среднее значение, определенное по уравнению регрессии

(6.173);

y - оценка генерального среднего Y (среднее всей совокупности).

Вычислим Y2 = 1197,3 / 50 – (241,2 / 50)2 = 0,675 и y =

241,2/50 = 4,82.

Необходимые промежуточные расчеты для вычисленияY2|x приведены в таблице 6.34. Следовательно, межгрупповая

дисперсия равна Y2|x = 25,911 / 50 = 0,518 и показатели тесноты

связи равны: 2	= 0,518 / 0,675 = 0,767 и	T		2	= 0,876.
T		T		T

Для расчета эмпирического корреляционного отношения воспользуемся формулой (6.190). Необходимые промежу-

точные расчеты для вычисления Y2|x приведены в таблице 6.34. Так как общая дисперсия не зависит от формы связи, то sy2 Y2 = 0,675. Тогда оценка межгрупповой дисперсии рав-

на y2|x = 27,638 / 50 = 0,553 и показатели тесноты связи рав-


ны:	2	= 0,553 / 0,675 = 0,819 и	2 = 0,905.
ны:	2	= 0,553 / 0,675 = 0,819 и	2 = 0,905.

Из анализа теоретических и эмпирических показателей тесноты связи следует, что связь между переменными Y и X сильная (см. таблицу 6.27). Теоретическое корреляционное

отношение меньше эмпирического, т.е. T2 2 , следова-

237

тельно, эмпирическое корреляционное отношение завышает тесноту связи.

Особое значение для теории и практики эксплуатации (но и для других областей деятельности человека) имеет исследование теоретического корреляционного отношения для случая линейной связи между факторным и результативным

признаками (см. ф. (6.163)).

Покажем, что коэффициент корреляции является част-

ным

случаем

теоретического

корреляционного

отношения.

M y Y 2

имеем

Согласно (6.187)

. Так

n 2

y n a0 a1 x в соответствии с пер-

как

, а

вым

уравнением

системы

нормальных уравнений (6.166),

a1 x ,

где x 1 n x . Следовательно,

a0 a1 x a0

a1 x 2

a12 x x

2 x2

a1 2 .

n 2

С целью дальнейшего преобразования последнего вы-

ражения заменим коэффициент регрессии а1

на его выражение

n yx x y

(см. ф. (6.167)), затем разделим его числи-

тель

знаменатель

на

и,

учитывая,

что

, окончательно получим

2T2 a12 x2

n yx x y

x y

2 2

y .

x 2

Следовательно, теоретическое корреляционное отношение для линейной парной регрессии

	1			xy		2
2					xy .		(6.195)
T	2	2
	x	y	n

Из последнего выражения следует, что

1 r 1. (6.198)

Если коэффициент корреляции положительный r > 0, то связь между переменными положительная, т.е. с увеличением значений х увеличивается у. Если коэффициент корреляции отрицательный r < 0, то связь между переменными отрицательная, т.е. с ростом х величина у уменьшается.

Отметим еще одно свойство коэффициента корреляции: коэффициент корреляции не зависит от выбора начала отсчета переменных и единиц измерения, т.е. r a01x b11; a02 x b12 r x, y .

238

Извлекая квадратный корень из (6.195), получим выра-

жение для определения выборочного (эмпирического) коэф-

фициента корреляции

x x y y

. (6.196)

x y

В самом деле,

x x y y

xy yx xy

nxy

из чего следует выражение (6.196).

При малом числе наблюдений коэффициент корреляции

удобно вычислять по формуле

n xy x y

(6.197)

x 2 n

y 2

Важным свойством коэффициента корреляции является то, что его значения находятся в интервале [- 1, +1]. Для доказательства этого свойства исследуем явно неотрицательное выражение

1	x x		y y	2
				0.
n		x	x

Возведем выражение под знаком суммы в квадрат

	1	x x	2		1	x x y y			1	2
	1	x x		2	1	x x y y			1	y y	0.
		2					x y			2
		2			n				n	2
n		x			n				n	y

Так как 1 n x x 2							x2 и	1 n y y 2 y2 , то

первое и третье слагаемые равны единице, и выражение преобразуется

1 2r 1 0 .

239

Следовательно, переменные х и у можно уменьшать или увеличивать в α раз, а также вычитать (или прибавлять) к значениям х и у одно и то же число β.

Если коэффициент корреляции r(x, y) = 0, то случайные величины некоррелированы. Некоррелированность не означает независимость: независимые случайные величины всегда некоррелированы. Обратное утверждение неверно: некоррелированные величины могут быть зависимы и даже функцио-


нально зависимы.
	Для линейной парной регрессии, по данным таблицы
6.28, вычислить коэффициент корреляции.
	Все необходимые суммы приведены в таблице 6.28:
xy	= 37175,0; x = 735,0; y = 7110;		x2 = 4053,5;
y 2	= 363950,0.
Тогда по формуле (6.197)
r		150 37175,0 735,0 7110		0,67 .

150 4053,5 735,02 150 363950,0 71102

Коэффициент корреляции часто используют при нелинейных связях. Если предварительный графический анализ указывает на какую-либо тесноту связи, то полезно вычислить

коэффициент корреляции. Если r > 0,8, то можно с уверен-

ностью считать, что независимо от вида связи, она достаточна тесна для того, чтобы исследовать ее форму.

Точечной оценкой коэффициента корреляции ρ является эмпирический коэффициент корреляции r. Однако эмпирический коэффициент корреляции r является надежной оценкой ρ лишь при достаточно близком к нормальному распределению случайных величин X и Y. В этом случае, эмпирический коэффициент корреляции имеет распределении с параметрами ρ и σr, близкое к нормальному. Зная закон распределения r, можно найти доверительные интервалы для коэффициента корреляции ρ:

r tq r r tq r ,

(6.199)

где r – эмпирический коэффициент корреляции; tq – параметр распределения Стьюдента;

σr – среднее квадратическое отклонение r. Оценка для σr вычисляется по формуле

	s		1 r		2	.
r		r

				n

240

Подставив это выражение в (6.199), получим

r tq	1 r 2		r tq	1 r		2	.	(6.200)

		n			n

Найдем доверительные интервалы для коэффициента кор-

реляции для линейной парной регрессии, по данным таблицы
6.28. Для r=0,67 и n=150 имеем				1 0,672	/
	r	s	r			150 0,045.

Для доверительной вероятности р = 0,95 и n = 150 для распределения Стьюдента (Приложение В) tq = 1,96. доверительный интервал равен: 0,582 < ρ < 0,758. Следовательно, с вероятностью р = 0,95 коэффициент корреляции будет находиться в рассчитанных границах.

В случае небольшого числа наблюдений (n < 30) распределение эмпирического коэффициента корреляции существенно отличается от нормального. В этом случае для оценки коэффициента корреляции применяется найденное Фишером преобразование, при котором эмпирический коэффициент корреляции приравнивается гиперболическому тангенсу некоторой величи-

ны z: r thz, откуда	z	1	ln	1 r	. Распределение величины z не

		2		1 r

зависит от значений ρ и n; с ростом числа наблюдений n распределение быстро приближается к нормальному.

При корреляционном анализе возникает необходимость оценить достоверность связи между переменными, т.е. выяснить, не объясняется ли величина коэффициента корреляции, полученная по выборочным данным, случайностями выборки. Для этого оценивается значимость (или существенность) коэффициента корреляции. Выдвигается гипотеза Н0 о том, что ρ = 0 и альтернативная гипотеза Н1, что ρ ≠ 0.

При большом объеме выборки величин r / r подчиняет-

ся нормальному закону распределения, поэтому проверка значимости (или существенности) коэффициента корреляции сводится

к следующему: вычисляется значение t r / r , которое затем

сравнивается со значением tq, найденным по распределению Стьюдента (Приложение В) для заданной вероятности р.

Если t < tq, то принимается гипотеза Н0, т. е. коэффициент корреляции считать существенным нельзя и его появление объясняется случайностями выборки. Если t > tq, то гипотеза Н0 отвергается и коэффициент можно считать существенным, а связь между случайными переменными X и Y достоверной.

241

Оценим существенность коэффициента корреляции для линейной парной регрессии. Для r = 0,67 и r = 0,045 имеем t = |r| / r = 0,67 / 0,045 =14,9. Так как для доверительной вероятности р = 0,95 параметр tq =1,96. Так как t >> tq, то коэффициент корреляции является существенным, а связь достоверной.

Доверительные интервалы для коэффициентов регрессии вычисляются по формуле

a tq a a tq a ,

(6.201)

где a – коэффициенты регрессии, полученные при решении системы нормальных уравнений;

a –среднее квадратическое отклонение коэффициента регрессии; tq – параметр распределения Стьюдента.

Среднее квадратическое отклонение коэффициента регрессии вычисляется

a	y	1 r		2	,	(6.202)
	x
			n

где y и x – средние квадратические отклонения результативного и факторного признаков;

r – эмпирический коэффициент корреляции; n - число измерений.

Оценим доверительный интервал для коэффициента парной линейной регрессии. Необходимые суммы для вычисления y и x имеются в таблице 6.28:

y
			1				y 2		y 2					1
			1		n									1			150 363950 71102			13,40 ,
			n		n								150				150 363950 71102			13,40 ,
			n										150
	x
	x
				1				x2		x 2					1
				1		n									1			150 4053,5 7352		1,73 .
						n												150 4053,5 7352		1,73 .
				n									150
		По формуле (6.202) находим
												13,40				1		0,67	0,348 .
										a									0,348 .

											1,73						150
											1,73						150

Для доверительной вероятности р = 0,95 и n = 150 для распределения Стьюдента (Приложение В) tq = 1,96. Для коэффициента регрессии а1 = 5,40 доверительный интервал

5,40 – 1,96 0,348 < a1 < 5,40 + 1,96 0,348 или 4,72 < a1 < 6,08.

Следовательно, с вероятностью р = 0,95 коэффициент регрессии находится в указанных пределах.

Во множественном регрессионном анализе взаимосвязь между случайными переменными усложняется. Парный коэффициент корреляции rij между i-й и j-й случайными величи-

242

нами может не соответствовать действительности. Например, положительная корреляция между переменными xi и xj может быть обусловлена их зависимостью от xk, в то время как при фиксированном xk эти величины стохастически независимы. Следовательно, при изучении связи между переменными xi и xj необходимо исключить влияние xk, т.е. оценить тесноту связи при фиксированном xk.

В общем случае для k факторных признаков для оценки тесноты связи имеем выражение для условного коэффициента корреляции величин xi и xj без учета влияния величины xk

rij.k	rij rik rjk		.	(6.203)

	1 r 2	1 r 2
	ik	jk

где rij, rik, rjk – парные коэффициенты корреляции.

Поскольку исключено влияние только одной переменной, то коэффициент корреляции rij.k называется частным

коэффициентом корреляции первого порядка.

Пусть имеем три случайные величины x1, x2 и x3. Оценим тесноту связи между x1 и x2 при фиксированном x3 с помощью парных коэффициентов корреляции

r12.3	r12 r13r23		,	(6.203)

	1 r 2	1 r 2
	13	23

где r12, r13, r23 – парные коэффициенты корреляции. Действительно, в случае независимости x1 и x2 от x3 име-

ем r13 = r23 = 0. Тогда из (6.203) следует, r12.3 = r12.

В случае четырех переменных x1, x2, x3, x4 можно вычис-

лить частные коэффициенты корреляции первого и второго порядка. Коэффициенты корреляции первого порядка вычисляются по (6.203), а второго – по

r12.34	r12.3 r14.3r24/ 3			,	(6.205)

	1	r 2	1 r 2
		14.3	24.3

где r12.3, r14.3, r24.3 – частные коэффициенты корреляции первого порядка.

Для данных (таблица 6.34) рассчитаем частные коэффициенты корреляции между у и х1, исключив влияние х2.

Имеем ryx1 = -0,811, ryx2 = - 0,586, rx1x2 = 0,502, тогда по

формуле (6.204)

243

ryx .x		0,811 0,586 0,502				0,738 .


	2		1	0,586 2	1 0,5022
1	2

Очевидно, что частный коэффициент корреляции ryx1.x2 между у и x1 по абсолютной величине меньше абсолютной величины парного коэффициента корреляции ryx1 между теми

же переменными.

Таблица 6.34 - К расчету теоретического корреляционного отношения

			Теоретическое корреляционное								Эмпирическое
			Теоретическое корреляционное								корреляционное
x	mx				отношение						корреляционное
					отношение						отношение


		y	y	y	y	y	2 mx	yi(x)	yi (x)	y	yi (x)	y	2 mx
5	8	6,16	1,332		14,194			6,05	1,226		12,025
7	9	5,31	0,482		2,088			5,29	0,466		1,954

9	6	4,83	0,009		0,001			5,20	0,376		0,848
11	8	4,53	-0,291		0,679			4,50	-0,324		0,840
13	6	4,32	-0,499		1,496			4,53	-0,294		0,519

15	5	4,17	-0,652		2,126			4,16	-0,664		2,204
17	4	4,06	-0,769		2,364			3,80	-1,024		4,194
19	4	3,96	-0,861		2,964			3,70	-1,124		5,054

	= 50				= 25,911						= 27,638

Теснота связи в случае множественной регрессии оце-

нивается также корреляционным отношением, которое в случае линейной связи называется множественным или со-

вокупным коэффициентом корреляции, а именно

					R 2
					R 2						2	/ 2	,				(6.206)
								y. x1x2			y. x1x2	y
								y. x1x2			y. x1x2
где	2		- корреляционное отношение;
	y . x1x2
				2		1				2			1			2
				2		1				2			1			2
		y . x x					yx1x2		y ;			y2			y	y	;
						n
						n								n
				1 2
		yx x a0 a1x1 a2 x2 ;								y a0 a1x1 a2 x2 .
		1		2

Коэффициент множественной корреляции выражает точность прогноза факторного признака по линейному уравнению регрессии.

Запишем без вывода часто употребляемые выражения для коэффициента множественной корреляции:

<<< < Предыдущая 28 29 30 31 32 33 34 35 36 37 38 3940 / 5440 41 42 43 44 45 46 47 48 49 50 51 52 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.05.201587.63 Кб340Введение экзамен.docx
#
15.05.201551.68 Кб19вексель и чек.rtf
#
21.11.2018506.88 Кб6Велик. для Фомичева.doc
#
18.03.201630.48 Кб8Виды договоров.docx
#
15.05.2015150.29 Кб28ВКР Сушков.docx
#
15.05.20154.39 Mб971ВКР-2010(Поляков).pdf
#
11.08.20193.15 Mб7Владимирские-работа.doc
#
24.09.2019460.29 Кб7Власть и СМИ. ПР-Технологии Реком. к экз.doc
#
15.05.201554.78 Кб6Возобновляемые источники энергии.doc
#
15.05.201517.21 Кб314войны людовика 14 таблица.docx
#
15.05.201584.99 Кб20волго-вятский экономич район.doc