201
6.7.2Однофакторный комплекс
Впрактике эксплуатации возможен случай, когда имеются материалы или однотипные изделия (детали, узлы, агрегаты и т.п.), находящиеся на хранении в нескольких хранилищах, имеющих различные условия хранения. При проведении контрольных испытаний установлено, что они имеют различные показатели качества, например, плотность, вязкость и другие показатели. Здесь имеет место один фактор – условия в хранилище (условия хранения). Исследователя интересует вопрос, существенно ли влияние этого фактора на показатели качества материалов? Ответ на этот вопрос можно получить, сравнивая средние значения показателя свойства по каждому хранилищу между собой и оценки существенности разницы этих средних.
Предположим, что из m хранилищ произведены выборки по n единиц материала (деталей), находящихся на хране-
нии. Обозначим выборку из i-й совокупности (xi1, xi2, …, xij, …, xin,). Тогда все выборки можно записать в виде следующей таблицы, которая называется матрицей наблюдений (таблица 6.21). Показатель свойства материала или детали имеет нормальное распределение.
Таблица 6.21 - Матрица наблюдений
Количество совокупностей (выборок) m
|
Количество элементов в совокупно- |
Средние арифме- |
||||||||||||||||
|
|
|
сти (выборке) n |
|
|
|
||||||||||||
|
|
|
|
|
|
тические групп |
||||||||||||
|
1 |
|
2 |
… |
j |
|
… |
|
n |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
||
1 |
x11 |
|
x12 |
… |
x1j |
|
x1n |
|
x1n |
x1* |
|
|
|
x1 j |
||||
|
|
n |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
||
2 |
x21 |
|
x22 |
… |
x2j |
|
x2n |
|
x2n |
x2* |
|
|
|
x2 j |
||||
|
|
|
|
n |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
||
… |
… |
|
… |
… |
… |
|
… |
|
… |
|
|
|
|
… |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
||
i |
xi1 |
|
xi2 |
… |
xij |
|
xin |
|
xin |
xi* |
|
|
|
xij |
||||
|
|
|
|
n |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
||
… |
… |
|
… |
… |
… |
|
… |
|
… |
|
|
|
|
… |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
||
m |
xm1 |
|
xm2 |
… |
xmj |
|
… |
|
xmn |
xm* |
|
|
|
xmj |
||||
|
|
|
|
n |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
||
Средняя арифметическая всех групп |
|
|
|
|
1 |
|
|
|
m |
|||||||||
|
|
(совокупностей) |
|
|
|
x |
|
|
|
|
xi* |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
m i 1 |
|||||||||||
202
Средние значения этих выборок обозначим 1, 2, …, i, …, m. Теперь проверим гипотезу о равенстве этих средних. Нулевую гипотезу запишем в виде Н0: 1 = 2 = …= i =…= m;
альтернативную – Н1: 1 2 … i … m.
Гипотеза Н0 проверяется сравнением внутригрупповых и межгрупповых дисперсий по F – критерию. Известно, что если случайная величина распределена по нормальному закону, то отношение выборочных дисперсий имеет распределение Фишера (или F- распределение). Если расхождение между дисперсиями незначительно, то нулевая гипотеза принимается. В противном случае гипотеза о равенстве средних отвергается и делается заключение о том, что различие в средних обусловлено не только случайностями выборок, но и действием исследуемого фактора. Рассмотрим структуру внутригрупповой и межгрупповой дисперсий и способ их вычислений. Вначале найдем средние арифметические каждой совокупности (выборки) и общую среднюю:
средняя арифметическая совокупности (выборки, группы)
|
|
1 |
n |
|
|
|
xi* |
|
xij |
; |
(6.129) |
||
n |
||||||
|
|
j 1 |
|
|
общая средняя всех совокупностей (выборок)
|
1 |
m n |
1 |
m |
|
|
x |
xij |
xi* ; |
(6.130) |
|||
|
|
|||||
|
mn i 1 j 1 |
m i 1 |
|
|||
Для вывода основного тождества дисперсионного анализа найдем сумму квадратов отклонений xij от x 29
|
m |
n |
xij |
m |
n |
xi* xi* x 2 |
|
|
|
x 2 xij |
|||||
|
i 1 |
j 1 |
|
i 1 |
j 1 |
|
(6.131) |
m n |
|
|
|
m n |
|
m n |
xi* xi* x . |
xij |
xi* 2 xi* x 2 2 xij |
||||||
i 1 j 1 |
|
|
|
i 1 j 1 |
|
i 1 j 1 |
|
Покажем, что последнее слагаемое тождества (6.131) равно нулю. Известно, что сумма отклонений переменных одной совокупности от средней арифметической этой же со-
вокупности равна нулю, т.е. n xij x1* 0 . Тогда
j 1
29 При преобразовании тождества (6.131) к выражению в скобках прибавили и отняли xi* .
203
S m n |
x |
ij |
x |
i* |
x |
i* |
x |
n x |
ij |
x |
m x |
i* |
x 0 |
m x |
i* |
x 0 |
|
|
|
|
|
|
|
|
|
i* |
|
|
|
||||||
i 1 j 1 |
|
|
|
|
|
|
|
j 1 |
|
|
|
i 1 |
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
Так как второй член тождества (6.131) не изменяется по |
|||||||||||||||||
индексу j, то его запишем в виде |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
m |
n |
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
xi* x 2 |
n xi* x 2 . |
|
|
|
||||||
|
|
|
|
|
|
|
i 1 |
j 1 |
|
|
|
i 1 |
|
|
|
|
|
С учетом этих преобразований основное тождество дис- |
|||||||||||||||||
персионного анализа можно представить в виде |
|
|
|
||||||||||||||
|
|
|
|
|
m |
n |
|
|
|
m |
|
|
m n |
, |
|
(6.132) |
|
|
|
|
|
|
xij |
x 2 n xi* x 2 |
xij xi* 2 |
|
|
||||||||
|
|
|
|
|
i 1 j 1 |
|
|
i 1 |
|
i 1 j 1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
Q |
|
|
|
Q1 |
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q Q1 Q2 , |
|
|
|
|
(6.133) |
||||
Компоненты тождества имеют собственные названия и |
|||||||||||||||||
определяются по формулам: |
|
|
|
|
|
|
|
|
|||||||||
общая или полная сумма квадратов отклонений от- |
|||||||||||||||||
дельных наблюдений от общей средней x |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
m |
n |
|
x 2 ; |
|
|
|
|
||
|
|
|
|
|
|
|
Q xij |
|
|
|
(6.134) |
||||||
|
|
|
|
|
|
|
|
i 1 |
j 1 |
|
|
|
|
|
|
|
|
сумма квадратов отклонений между группами |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q1 n xi* |
x 2 ; |
|
|
|
|
(6.135) |
||||
i 1
сумма квадратов отклонений внутри группы
m |
n |
xi* 2 . |
|
Q2 xij |
(6.136) |
||
i 1 |
j 1 |
|
|
Слагаемое Q1 характеризует систематическое расхождение между совокупностями (группами) наблюдений, ее часто называют рассеиванием по факторам (т.е. за счет исследуемого фактора). Слагаемое Q2 характеризует остаточное рассеивание случайных погрешностей совокупностей (групп).
Оценки дисперсий определяются по формулам:оценка полной (общей) дисперсии
|
|
|
m |
n |
|
|
|
|
s 2 |
1 |
|
xij x 2 |
|
Q |
; |
(6.137) |
|
mn 1 |
|
|||||||
|
i 1 |
j 1 |
|
mn 1 |
|
|||
|
|
|
|
|
|
|
||
оценка межгрупповой дисперсии
204
|
|
|
1 |
|
m |
|
|
Q1 |
|
|
|
|
|
|
|
|||
|
s12 |
|
|
xi* |
x 2 |
|
|
. |
|
|
|
|
(6.138) |
|||||
m 1 |
m |
|
|
|
|
|
||||||||||||
|
|
|
i 1 |
|
1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оценка внутригрупповой дисперсии |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
m |
n |
|
|
|
|
Q2 |
|
|
|
|
|
||
s22 |
|
1 |
|
|
xij |
xi* 2 |
|
|
|
|
|
; |
(6.139) |
|||||
m n 1 |
|
m n 1 |
||||||||||||||||
|
i 1 |
j 1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отношение дисперсий выборок |
s 2 |
|
и |
s |
2 |
, так называе- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
||
мый показатель достоверности,
|
s 2 |
|
Q |
m 1 |
(6.140) |
|
F s 2 |
|
Q m n 1 |
|
|||
1 |
|
1 |
|
|
|
|
2 |
|
2 |
|
|
|
|
подчиняется распределению Фишера (F-распределение) со степенями свободы k1=(m-1) и k2=m(n-1) (Приложение Г). Распределение Фишера позволяет при заданных объемах выборок вычислить вероятность того, отношение дисперсий превзойдет некоторое заданное число F . Если эта вероятность окажется достаточно малой, то соответствующее число F можно считать пограничным показателем достоверности в том смысле, что в случайных выборках отношение дисперсий практически не должно превзойти его (по принципу практической невозможности маловероятных событий). В теории статистики принимают три уровня «достаточно малой» вероятности, которые соответствуют классификации явлений на редкие (=0,05), очень редкие (=0,01), чрезвычайно редкие (=0,001).
Выбирая уровень значимости , найдем соответствующий предел так, чтобы
P(F > F ) = , |
(6.141) |
где F и F - расчетное и табличное значения отношения дисперсий;
P(F > F ) – вероятность события, когда расчетное значение критерия больше табличного.
Если расчетное значение отношения больше табличного, то гипотеза о равенстве средних отвергается и принимается альтернативная гипотеза, т.е. влияние фактора на результативный признак существенно.
Однофакторный дисперсионный анализ удобно представить в виде таблицы (таблица 6.22).
Таблица 6.22 - Таблица однофакторного дисперсионного анализа
Компоненты |
|
Число |
Оценка дисперсии (средний |
|
Сумма квадратов |
степеней |
|||
дисперсии |
квадрат) |
|||
|
свободы k |
|||
|
|
|
205
|
m |
|
|
|
|
|
|
|
|
1 |
|
|
m |
|
|||
Межгруп- |
Q1 n |
|
|
|
2 |
|
s12 |
|
|
|
xi* x 2 |
||||||
xi* |
x |
k1 = m -1 |
|||||||||||||||
повая |
|
|
|
||||||||||||||
i 1 |
|
|
|
|
|
|
|
|
m 1 i 1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
m n |
|
|
|
|
|
|
1 |
|
|
m n |
|
|||||
Внутриг- |
Q2 xij |
xi* 2 |
k2=m(n – 1) |
s22 |
|
|
xij |
xi* 2 |
|||||||||
рупповая |
|
|
|
|
|||||||||||||
i 1 j 1 |
|
|
|
|
|
m n 1 i 1 j 1 |
|
||||||||||
|
|
|
|
|
|
|
|||||||||||
|
m n |
|
|
|
|
|
|
|
|
|
|
|
m n |
|
|||
Полная |
Q xij |
x 2 |
k = mn – 1 |
s 2 |
1 |
|
xij |
x 2 |
|||||||||
(общая) |
|
|
|
|
|||||||||||||
i 1 j 1 |
|
|
|
|
|
|
|
mn 1 i 1 j 1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
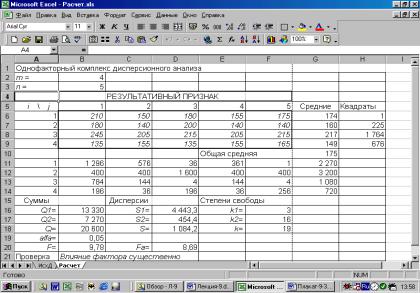
Применение однофакторного комплекса проиллюстрируем следующим примером. Пусть имеются 4 хранилища с различными условиями хранения, из которых выбрано по 5 образцов материала и проведены контрольные испытания на определение результативного признака, например, разрывной нагрузки (таблица 6.23).
Таблица 6.23 - Исходные данные для однофакторного комплекса
|
|
|
|
|
|
|
|
Количество элементов в сово- |
Средние арифмети- |
||||||||||
|
|
|
|
|
|
|
|
купности (выборке) n =5 |
|
||||||||||
|
|
|
|
|
|
|
|
|
ческие выборок |
||||||||||
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
4 |
|
5 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Количество совокупностей выборок( ) =m4 |
|
1 |
|
|
|
210 |
|
150 |
180 |
155 |
|
175 |
x1* |
= 174 |
|||||
|
2 |
|
|
|
180 |
|
140 |
200 |
140 |
|
140 |
x2* |
= 160 |
||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
3 |
|
|
|
245 |
|
205 |
215 |
205 |
|
215 |
x3* |
= 217 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
4 |
|
|
|
135 |
|
155 |
135 |
155 |
|
165 |
x4* |
= 149 |
||||
Средняя арифметическая всех совокупностей |
|
x = 175 |
|||||||||||||||||
|
Средние арифметические вычислены по формулам |
||||||||||||||||||
(6.129) и (6.130): |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
|
5 |
|
|
|
|
|
|
|
|
|
|
||
x1* |
|
|
x1 j |
= 1 / 5 (210 + 150 + 180 + 155 + 175) = 174; |
|||||||||||||||
5 |
|
||||||||||||||||||
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
5 |
|
|
|
|
|
|
|
|
|
|
||
x2* |
|
|
x2 j |
= 1 / 5 (180 + 140 + 200 + 140 + 140) = 160; |
|||||||||||||||
5 |
|||||||||||||||||||
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
5 |
|
|
|
|
|
|
|
|
|
|
||
|
x3* |
|
|
x3 j |
= 1 / 5 (245 + 205 + 215 + 205 + 215) = 217; |
||||||||||||||
|
5 |
|
|||||||||||||||||
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
5 |
|
|
|
|
|
|
|
|
|
|
||
x4* |
|
|
|
|
x4 j |
= 1 / 5 (135 + 155 + 135 + 155 + 165) = 149; |
|||||||||||||
|
5 |
|
|||||||||||||||||
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
xi* = 1 / 4 (174 + 160 + 217 + 149) = 175. |
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
4 i 1 |
|
|
|
|
|
|
|
|
|
||||||
206
Суммы квадратов и оценки дисперсий вычислены по формулам (6.134) – (6.136) и по (6.137) – (6.139) и сведены в таблицу (таблица 6.24).
Таблица 6.24 - Результаты расчетов для однофакторного комплекса
Компоненты |
Сумма |
Число |
Оценка |
|
степеней |
дисперсии |
|||
дисперсии |
квадратов |
|||
свободы |
(средний квадрат) |
|||
|
|
|||
Межгрупповая |
13330 |
3 |
4443,3 |
|
Внутригрупповая |
7270 |
16 |
454,4 |
|
Полная (общая) |
20600 |
19 |
1084,2 |
По формуле (6.140) определяем расчетное значение F = 4443,3 / 454,4 = 9,78; для уровня значимости = 0,05 и степеней свободы k2 = 16 и k1 = 3 табличное значение F = 8,69. Так как F > F, то нулевая гипотеза отвергается и делается вывод о том, что влияние условий хранения на результативный признак существенно.
Пример дисперсионного анализа однофакторного комплекса с использованием табличного процессора MS Exsel приведен на рисунке 6.42. Здесь приведены пояснения содержания ячеек процессора. Следует отметить, что определение теоретического значения показателя F производится с ис-
пользованием встроенной функции FРАСПОБР(; s12 ; s22 ).
Рисунок 6.42 - Окно табличного процессора MS Exsel с дисперсион-