
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •1 ИТОГОВАЯ ГОСУДАРСТВЕННАЯ АТТЕСТАЦИЯ ВЫПУСКНИКОВ В СИСТЕМЕ ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
- •1.1 Основные сведения о системе образования
- •1.2 Система высшего и послевузовского профессионального образования
- •1.3 Итоговая государственная аттестация
- •2 ТИПОВАЯ СТРУКТУРА И ТРЕБОВАНИЯ К ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЕ
- •3 ВОЕННО-НАУЧНОЕ ОБОСНОВАНИЕ ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЫ
- •3.1 Место вооружения Космических войск в системе военно-технических средств ВС РФ
- •3.1 Структура военно-научного обоснования темы ВКР
- •3.2 Методика оперативно-тактического обоснования системы вооружения
- •4 ТРЕБОВАНИЯ И РЕКОМЕНДАЦИИ ПО ОФОРМЛЕНИЮ УЧЕБНЫХ ТЕКСТОВЫХ ДОКУМЕНТОВ И ДЕМОНСТРАЦИОННЫХ ПЛАКАТОВ
- •4.1 Назначение и виды учебных текстовых документов
- •4.2 Общие требования к учебным текстовым документам
- •4.3 Титульный и заглавный листы, содержание
- •4.4 Построение документа
- •4.5 Изложение текста
- •4.5.2 Нормативные требования к тексту
- •4.6 Примечания, ссылки, сноски, примеры
- •4.7 Формулы в тексте
- •4.8 Таблицы
- •4.9 Иллюстрации
- •4.10 Приложения
- •4.11 Библиографическое описание произведений печати
- •4.12 Рекомендации по оформлению демонстрационных плакатов
- •5 ПОДГОТОВКА РАСЧЕТОВ И ИХ ВЫПОЛНЕНИЕ
- •5.1 Выбор показателя эффективности
- •5.2 Подготовка исходных данных
- •5.3 Определение точности и надежности оценок
- •5.4 Оценка погрешности расчетов
- •5.5 Запись приближенных чисел
- •5.6 Округление чисел
- •5.7 Предельная погрешность функции
- •5.8 Оценка влияния приращений аргументов на приращение функции
- •6 ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ УПРАВЛЕНИЯ ЭКСПЛУАТАЦИЕЙ ВООРУЖЕНИЯ КВ
- •6.1 Управление процессами эксплуатации вооружения КВ с использованием методов сетевого планирования и управления
- •6.1.1 Основные элементы сетевого графика
- •6.1.2 Правила построения сетевых графиков
- •6.1.3 Характеристики сетевого графика
- •6.1.4 Анализ и оптимизация сетевого графика
- •6.2 Управление эксплуатацией вооружения КВ с использованием методов математического программирования
- •6.2.1 Основные понятия и определения линейного программирования
- •6.2.2 Задача распределения оружия по носителям
- •6.2.3 Транспортная задача линейного программирования
- •6.3 Прогнозирование показателей технического состояния вооружения КВ с использованием временных рядов
- •6.3.1 Прогнозирование: основные понятия и определения
- •6.3.2 Характеристики временного ряда
- •6.3.3 Исследование динамического ряда
- •6.3.4 Прогнозирование показателей технического состояния вооружения КВ
- •6.4 Исследование связи процессов в системе эксплуатации с использованием взаимосвязанных динамических рядов
- •6.4.2 Алгоритм исследования взаимосвязанных динамических рядов
- •6.5 Статистическая оценка показателей эксплуатационных свойств вооружения КВ
- •6.5.1 Выбор закона распределения случайной величины
- •6.5.2 Расчет параметров распределения случайной величины
- •6.5.3 Выравнивание статистического ряда
- •6.5.4 Проверка правдоподобия гипотезы о выборе закона распределения случайной величины
- •6.5.5 Алгоритм статистической оценки показателя эксплуатационного процесса
- •6.6 Метод экспертных оценок показателей эксплуатационных свойств вооружения КВ
- •6.6.1Сущность и содержание метода экспертных оценок
- •6.6.2 Алгоритм применения метода экспертных оценок
- •6.7.1 Общая идея дисперсионного анализа
- •6.7.2 Однофакторный комплекс
- •6.7.3 Двухфакторный комплекс
- •6.8.2 Парная линейная регрессия
- •6.8.3 Парная нелинейная регрессия
- •6.8.4 Множественная регрессия
- •6.8.5 Оценка тесноты связи и значимости коэффициентов регрессии
- •6.9 Прогнозирование состояния системы с использованием марковских процессов и уравнений Колмогорова
- •ЗАКЛЮЧЕНИЕ
- •СПИСОК ЛИТЕРАТУРЫ
- •1. Руководящие и нормативные документы
- •2. Методические материалы
- •3. Дополнительная литература
- •Приложение А
- •Е.1 Основные сведения о Государственной системе стандартизации
- •Е.2 Виды стандартов
- •Е.4 Межотраслевые системы (комплексы) стандартов
- •Е.5 Комплекс стандартов «Государственная система стандартизации РФ»
- •Е.6 Единая система конструкторской документации
- •Е.7 Единая система технологической документации
- •Е.8 Система показателей качества продукции
- •Е.9 Унифицированные системы документации
- •Е.10 Система стандартов по информации, библиотечному и издательскому делу
- •Е.11 Государственная система обеспечения единства измерений
- •Е.12 Единая система защиты от коррозии и старения материалов и изделий
- •Е.13 Комплексы стандартов по безопасности жизнедеятельности
- •Е.14 Система стандартов «Репрография. Микрография»
- •Е.15 Система стандартов «Экологический менеджмент»
- •Е.16 Система разработки и постановки продукции на производство
- •Е.17 Единая система программных документов
- •Е.18 Система проектной документации для строительства
- •Е.19 Обеспечение износостойкости изделий
- •Е.20 Система технической документации на АСУ
- •Е.21 Система стандартов «Расчеты и испытания на прочность»
- •Е.22 Система стандартов «Надежность в технике»
- •Е.23 Система технического обслуживания и ремонта техники
- •Е.24 Система стандартов эргономических требований и эргономического обеспечения
- •Е.25 Комплекс стандартов «Единый российский страховой фонд документации»
- •Е.26 Комплекс стандартов «Информационная технология»
- •Е.27 Система сертификации ГОСТ Р
- •Е.28 Комплекс стандартов «Единообразные предписания …»
- •Е.29 Комплекс государственных стандартов гражданской обороны
- •Е.30 Информационное обеспечение техники и операторской деятельности
- •ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
181
* |
|
|
|
1 |
|
|
|
x mx |
|
f (xi |
|
f (x) |
|
|
|
||||
|
|
|
|
|
exp |
|
|
||
|
|
|
|
2 2 |
|||||
|
2 |
||||||||
|
|
|
|
|
|
|
|||
x1 |
x2 |
xk |
xk+1 |
x |
|
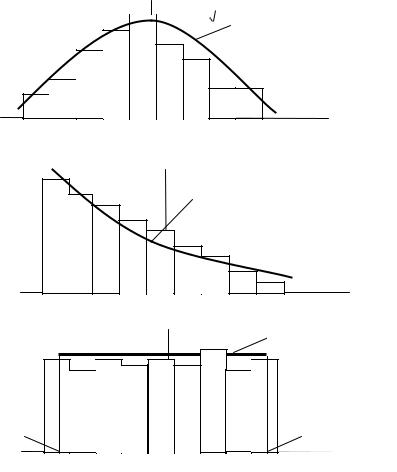
а) распределение, близкое к нормальному (Гаусса) |
|||
|
|
f*(xi) |
|
|
|
|
|
|
f(x) = exp ( - x) |
|
|
x1 |
x2 |
|
xk |
xk+1 |
x |
|
б) распределение, близкое к экспоненциальному |
|
|||
|
|
f*(xi) |
f(x) = 1 / ( - ) |
|
|
|
|
|
|
||
|
|
|
|
|
x1 |
x2 |
xk |
xk+1 |
x |
в) распределение, близкое к равномерному распределению |
||||
Рисунок 6.37 - Гистограммы статистических распределений |
||||
6.5.2 Расчет параметров распределения случайной величины
Каждой числовой характеристике случайной величины соответствует статистическая аналогия: математическому ожиданию – статистическое среднее; дисперсии - статистическая дисперсия; среднему квадратическому отклонению – эмпирический стандарт и т.д.
Если число опытов сравнительно невелико (n < 100), то статистические характеристики можно определить из простого статистического ряда по формулам:
182
- статистическое среднее
|
|
n |
|
|
mx 1 |
n |
xi |
, |
(6.94) |
|
i 1 |
|
|
|
|
|
|
|
- статистическая дисперсия
|
|
|
|
n |
|
|
|
x 1 |
|
(xi mx )2 . |
(6.95) |
D |
n |
||||
|
|
|
i 1 |
|
|
|
|
|
|
|
При большом количестве опытов (n > 100) для определения статистических характеристик целесообразно воспользоваться статистическим рядом. Тогда для числовых характеристик статистического распределения имеем:
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
mx x j p*j |
; |
(6.96) |
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
(x j mx )2 p*j , |
(6.97) |
||
|
|
|
|
|
|
|
Dx |
||||||
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
где |
x |
|
1 |
(x |
|
x |
j 1 |
) |
- «представитель» j-го разряда; сред- |
||||
|
|
j |
2 |
|
j |
|
|
|
|
|
|
||
нее значение j-го разряда.
6.5.3 Выравнивание статистического ряда
Во всяком статистическом распределении в силу ограниченности числа опытов присутствует элемент случайности. Только при большом числе опытов случайности сглаживаются и полностью проявляется закономерность. При подборе вида распределения следует учитывать только существенные черты статистического распределения. Следует отметить, что в настоящее время не существует критериев, по которым можно было бы без построения гистограмм классифицировать распределения по видам. Задача подбора теоретической кривой для статистического ряда называется задачей выравнивания (сглаживания) статистического ряда.
Вид теоретической кривой распределения выбирается либо из физической сущности исследуемого процесса, либо по внешнему виду гистограмм распределения. Отметим, что при выборе вида теоретической зависимости опыт, как и в любом виде деятельности, является определяющим.
Для гистограмм, приведенных на рисунке 6.37, можно рекомендовать к использованию:
- нормальное распределение (распределение Гаусса)

183
|
|
1 |
|
|
|
(x mx )2 |
|
; |
(6.98) |
f (x) |
|
|
|
exp |
|
|
|
||
|
|
|
|
||||||
|
|
2 x |
|
|
2 |
|
|
|
|
|
|
|
|
2 x |
|
|
|
||
- экспоненциальное распределение
0 |
при x 0; |
(6.99) |
f (x) |
|
|
e x при x 0; |
|
|
|
|
|
- распределение равномерной плотности
|
|
1 |
при x ; |
(6.100) |
||
|
|
|
||||
|
||||||
f (x) |
|
|
|
|||
0 |
при x |
и x , |
|
|||
|
|
|
|
|
|
|
где σx – среднее квадратическое отклонение; mx – математическое ожидание;
λ – интенсивность потока событий; α, β – границы интервала распределения СВ (для распреде-
ления равномерной плотности).
Пределы изменения случайной величины для распределения равномерной плотности определяются из уравнений:
mx |
|
и Dx |
|
( )2 |
. |
|
12 |
||||||
|
|
2 |
|
|
Решая эти уравнения, получим
|
|
|
|
|
|
mx |
|
и mx 3Dx . |
(6.101) |
||
3Dx |
|||||
Нормальный закон распределения (закон Гаусса) используется для описания большинства случайных величин в технике, природе; экспоненциальное распределение – для описания времени наработки до отказа; закон равномерной плотности – для описания случайных величин, вероятность появления которых примерно постоянна на данном интервале.
Следует отметить, что в науке и технике используется более десяти законов распределения [3.10].
Отметим, что гистограмма распределения может быть описана не только известными законами распределения, но и специфическими для данного распределения зависимостями. Подбор аналитических функций для гистограмм плотности может быть произведен методом наименьших квадратов. Но любая аналитическая функция f(x), с помощью которой выравнивается статистическое распределение, должно обладать основными свойствами плотности распределения:
|
184 |
|
f (x) 0; |
|
(6.102) |
|
f (x) dx 1. |
|
|
Предположим, что вид аналитической функции f(x) вы- |
|
бран. Известно, что в выражение этой функции входят несколько параметров a, b, c и т.д. Требуется подобрать эти параметры так, чтобы функция f(x) наилучшим образом описывала данный статистический материал. Согласно одному из методов подбора – методу моментов – параметры a, b, c выбирают с таким расчетом, чтобы несколько важнейших числовых характеристик (моментов) теоретического распределения были равны соответствующим статистическим характери-
стикам, например: mx |
|
mx ; Dx |
|
|
x |
|
и т.д. |
|
|||||||
D |
|
|
|||||||||||||
Для экспоненциального закона распределения, который |
|||||||||||||||
определяется одним параметром, имеем |
|
||||||||||||||
|
1 |
|
или |
|
1 |
. |
(6.103) |
||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||
|
|
Dx |
|
|
|
|
|
|
|
||||||
Для нормального закона и закона равномерной плотно- |
|||||||||||||||
сти, которые определяются двумя параметрами, - |
|
||||||||||||||
|
mx mx ; Dx |
|
|
x . |
|
(6.104) |
|||||||||
|
D |
|
|||||||||||||
6.5.4 Проверка правдоподобия гипотезы о выборе закона распределения случайной величины
Критерии согласия отвечают на вопрос о степени согласованности (соответствия) теоретического и статистического распределений. Одним из наиболее распространенных крите-
риев является критерий К. Пирсона, или критерий «хи - квад-
рат», или χ2 - квадрат.
К. Пирсон показал, что мера расхождения
|
k |
n p j ) |
2 |
|
|
|
|
|
|||
2 |
|
(m j |
|
(6.105) |
|
|
n p j |
|
|||
|
j 1 |
|
|
||
зависит только от числа «степеней свободы»
r = k – s, (6.106)
где k - число разрядов;
s - число независимых условий («связей»), наложенных на выбор теоретического распределения;
pj - вероятность попадания СВ в j - ый интервал.

185
Для экспоненциального закона распределения число связей s = 2, для нормального закона и закона равномерной плотности s = 3, а именно:
|
k |
|
|
|
1 я связь : p*j 1; |
(6.107) |
|||
j 1 |
|
|||
|
|
|||
2 я связь :mx |
mx ; |
|
||
|
|
|
||
3 я связь : |
D |
х |
Dx . |
|
Вероятности попадания СВ в j -ый интервал определяются
p j F(x j 1 ) F(x j ) . |
(6.108) |
Функция распределения определяется зависимостями: - для экспоненциального закона
0 |
при x 0; |
(6.109) |
F (x) 1 e x |
|
|
при x 0; |
|
|
|
|
|
- для закона равномерной плотности
|
0 |
|
при x ; |
(6.110) |
x |
|
|||
F (x) |
|
|
при x ; |
|
|
|
|||
|
|
|
||
|
1 |
при x . |
|
|
|
|
|
|
|
Если разряды одинаковы, то для закона равномерной плотности вероятности попадания в любой интервал одинако-
вы и равны pj = 1 / k.
Для нормального закона распределения вероятности попадания в j -ый интервал определяются по формуле
|
|
|
1 |
|
x |
j 1 |
m |
x |
|
x |
j |
m |
x |
|
|
||
p |
|
|
|
Ф |
|
|
|
Ф |
|
|
|
. |
|||||
j |
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
x |
|
|
|
|
x |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Значения функции Лапласа
|
2 |
|
|
|
Ф(x) |
|
e t 2 dt , |
||
|
|
|
||
|
|
|||
|
|
0 |
||
где t x mx .x
(6.111)
(6.112)
Значения функций Лапласа (Приложение Б) и распределения χ2 (Приложение Д) табулированы и приведены в руководствах по теории вероятностей, а также могут быть определены по встроенным функциям MS Excel ВЕРОЯТНОСТЬ(…) и ХИ2ОБР(Вероятность, степени свободы).
Фрагменты таблицы «Значения χ2 в зависимости от r и p» приведены в таблицах 6.12 и 6.13.
186
Используя таблицу «Значения χ2 в зависимости от r и p», для каждого значения χ2 и числа «степеней свободы» r можно найти вероятность того, что величина, распределенная по закону χ2, превзойдет фактическое значение этой величины.
Если вероятность р меньше вероятности нижней границы рн.г. = 0,1, т.е. р < рн.г., то выбранное теоретическое распределение не может быть принято. Если вероятность р больше вероятности верхней границы рв.г. = 0,9, т.е. р > рв.г., то следует исключить «подчистку данных», когда некоторые результаты изменяются или исключаются.
Пользоваться таблицей возможно двумя способами:
1 По числу «степеней свободы» r и значению χ2, полученному по формуле (6.105), определяют точное значение вероятности р. Если выполняется условие рн.г. < р < рв.г. , то выбранное теоретическое распределение может быть принято в качестве рабочей гипотезы. Для r = 8 и χ2 = 5,53 последовательность действий показана на номограмме (таблица 6.12).
Таблица 6.12 - Значения χ2 в зависимости от r и p (Фрагмент)
p |
0,99 |
… |
рв.г. = 0,9 |
… |
0,7 |
… |
рн.г. = 0,1 |
… |
0,001 |
r |
|
|
|
|
|
|
|
|
|
1 |
0,000 |
… |
0,016 |
… |
|
… |
2,71 |
… |
10,83 |
2 |
0,020 |
… |
0,211 |
… |
|
… |
4,60 |
… |
13,82 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
8 |
1,65 |
… |
3,49 |
2,82 |
5,53 |
… |
13,36 |
… |
21,6 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
2 Для верхней рв.г. = 0,9 и нижней рн.г. = 0,1 границ вероятностей и числа «степеней свободы» r определяют диапазон значений χ2. Если значение χ2, полученное по формуле (6.105) попадает в диапазон, то выбранное теоретическое распределение может быть принято в качестве рабочей гипотезы. Для r = 8 последовательность действий показана на номограмме (таблица 6.13).
Таблица 6.13 - Значения χ2 в зависимости от r и p (Фрагмент)
p |
0,99 |
… |
рв.г. = 0,9 |
… |
… |
… |
рн.г. = 0,1 |
… |
0,001 |
r |
|
|
|
|
|
|
|
|
|
1 |
0,000 |
… |
0,016 |
… |
… |
… |
2,71 |
… |
10,83 |
2 |
0,020 |
… |
0,211 |
… |
… |
… |
4,60 |
… |
13,82 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
8 |
1,65 |
… |
3,49 |
|
|
… |
13,36 |
… |
21,6 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
