115
4 этап. Проверка правильности построения сетевого графика. На этом этапе определяется, нет ли нарушений правил по строения сетевых графиков, т.е. отсутствие «тупиков», циклов и неправильного изображения параллельных работ.
Так как работы на графике изображаются безмасштабными стрелками, которые в свою очередь могут состоять из горизонтальных и наклонных участков, то отдельные участки графика напоминают многоугольники, и такая форма изображения сетевого графика называется полигональной.
Для разработанного сетевого графика составим таблицу всех работ с указанием порядковых номеров работ (см. таблица 6.1), новых обозначений работ (i,j), их продолжительностей tij, количества личного состава rij для выполнения каждой работы (таблица 6.2).
Таблица 6.2 – Таблица показателей работ сетевого графика
Порядковый |
Обозначение |
tij, |
rij, |
|
|
номер |
Примечание |
||||
работы (i,j) |
ч |
чел |
|||
работы |
|
||||
|
|
|
|
||
2 |
(1,2) |
0,5 |
2 |
|
|
4 |
(1,3) |
2,0 |
3 |
|
|
3 |
(1,4) |
1,0 |
2 |
|
|
1 |
(1,5) |
4,0 |
4 |
|
|
5 |
(2,4) |
1,0 |
3 |
|
|
|
(3,8) |
0 |
0 |
Фиктивная работа |
|
11 |
(3,10) |
1,0 |
3 |
|
|
|
(4,5) |
0 |
0 |
Фиктивная работа |
|
6 |
(4,7) |
1,5 |
3 |
|
|
7 |
(5,6) |
0,5 |
4 |
|
|
|
(6,7) |
0 |
0 |
Фиктивная работа |
|
|
(6,8) |
0 |
0 |
Фиктивная работа |
|
8 |
(7,9) |
1,0 |
4 |
|
|
9 |
(8,9) |
2,0 |
3 |
|
|
10 |
(9,10) |
3,0 |
3 |
|
|
12 |
(10,11) |
2,0 |
3 |
|
После построения сетевого графика производят расчет его характеристик.
6.1.3Характеристики сетевого графика
Косновным характеристикам сетевых графиков относятся ранний tр(i) и поздний tп(i) сроки наступления события,
резерв времени наступления события t(i), полный Rп(i,j) и
116
свободный Rс(i,j) резервы времени выполнения работ, время выполнения всего комплекса работ сетевого графика Ткр.
Так как исходными данными для определения этих характеристик являются времена выполнения отдельных работ tij, то охарактеризуем методы их определения.
Время выполнения работы. Для определения времени выполнения работы может быть использован либо детерминированный, либо стохастический (вероятностный) подходы.
При детерминированном подходе время выполнения работы считается неслучайной величиной и используется его однозначная оценка. При этом вопрос о неопределенности временных оценок не рассматривается. Такой подход может быть использован при выполнении комплекса работ, на которые имеются нормативы на выполнение работ, или там, где разброс времени выполнения работ пренебрежимо мал.
Если отсутствуют нормативы на выполнение, или отсутствует опыт выполнения подобных работ, то используется стохастический подход. В этих случаях время выполнения каждой работы считается случайным и для его оценки используется математические ожидания времени выполнения каждой работы.
Методика определения математического ожидания времени выполнения работы зависит от закона его распределения.
При выборе закона распределения времени необходимо учесть следующие особенности:
время выполнения любой работы ограничено как сверху, так и снизу, т.е. всегда можно указать максимальное время
tmax, в течение которого работа может быть выполнена при стечении самых неблагоприятных обстоятельств, и минималь-
ное время tmin, которое понадобится при наиболее благоприятном стечении обстоятельств;
время выполнения работы является непрерывной случайной величиной на интервале [tmin, tmax];
в комплексе работ имеются работы, время выполнения которых зависит от большого числа случайных факторов, каждый из которых в отдельности является малосущественным, а также работы, на выполнение которых оказывает влияние небольшое число существенных факторов.
Первая особенность требует, чтобы закон распределения
был усеченным на [tmin, tmax]; вторая – непрерывности закона распределения; третья – такого закона распределения, при ко-
117
тором наиболее вероятное значение времени выполнения работы могло располагаться в любом месте интервала [tmin, tmax].
Наиболее полно этим требованиям отвечает бетараспределение, плотность распределения которого имеет вид
t t |
min |
p 1 t |
max |
t q 1 |
|
|
t t |
|
|
|
|||
|
|
|
|
|
|
при t |
|
|
; |
|
|||
t |
|
t |
|
p q 1 B( p, q) |
|
|
, (6.1) |
||||||
f (t) |
max |
min |
|
min |
|
max |
|
||||||
|
|
|
0 при t tmin ,t tmax , |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
где tmin, tmax – границы интервала времени; p, q – параметры бета-распределения;
1
B p, q t p 1 1 t q 1 dt – бета-функция.
0
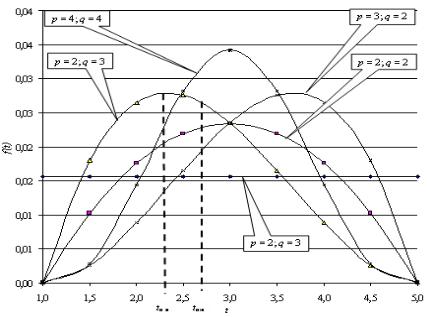
На рисунке 6.16 представлены графики плотности бетараспределения для различных значений параметров p, q. Так как графики построены с использованием математического процессора Mathcad 2000 Professional, то для расчетов использованы конкретные значения границ интервала, а именно: tmin= 1 ед. времени; tmax.= 5 ед. времени. Частным случаем бета-распределения при p = 1 и q = 1 является распределение равномерной плотности.
Рисунок 6.16 - Графики плотности бета - распределения:
118
t t |
min |
p 1 |
t |
max |
t q 1 |
t tmax |
|
|||
|
|
|
|
|
|
при tmin |
; |
|||
tmax |
|
|
|
|
|
|
||||
f (t) |
t min p q 1 B( p, q) |
|
|
|||||||
|
0 |
|
|
|
|
|
при t tmin ,t tmax , |
|
||
|
|
|
|
|
|
|
||||
где tmin, tmax – границы интервала времени (tmin =1,0; tmax= 5,0 ед. времени);
p, q – параметры бета - распределения;
1
B p, q t p 1 1 t q 1 dt – бета-функция.
0
Числовые характеристики бета-распределения определяются по формулам:
математическое ожидание времени выполнения работы
t |
|
t |
|
|
t |
|
|
t |
|
|
|
|
|
|
p |
; |
|
|
|
(6.2) |
||
ож |
min |
max |
min |
p q |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
наиболее вероятное время выполнения работы |
|
|||||||||||||||||||||
tн.в |
tmin |
tmax |
tmin |
|
|
|
|
|
p 1 |
|
; |
(6.3) |
||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
p |
q |
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
среднеквадратическое отклонение |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t tmax |
|
tmin |
|
|
|
|
|
|
pq |
|
|
|
. |
(6.4) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
( p q) |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
p q 1 |
|
|||||||||||
Для графика бета-распределения с параметрами p = 2 и q= 3 изображены наиболее вероятное время выполнения работы tн.в и математическое ожидание времени выполнения рабо-
ты tож.
Из анализа графика следует, что для несимметричного распределения с вершиной сдвинутой влево (p < q) наиболее вероятное время выполнения работы tн.в сдвинуто влево относительно математического ожидания времени выполнения работы tож, т.е. tн.в < tож. Аналогично, для симметричного распределения с вершиной сдвинутой вправо (p > q) можно сделать противоположный вывод: tн.в > tож.
Из анализа уравнений следует, что бета-распределение характеризуется семью параметрами tmin, tmax, tож, tн.в, t, p, q.
Три из них tmin, tmax, tн.в могут быть определены по методу экспертных оценок. Известно, что для одновершинных распреде-
119
лений среднеквадратическое отклонение примерно равно 1/6 интервала (правило «трех сигм»), т.е.
|
tmax tmin |
. |
(6.5) |
t |
6 |
|
Из сравнения (6.4) и (6.5) следует, что
|
pq |
|
1 |
. |
(6.6) |
||
|
|
|
|
|
|||
( p q) |
|
p q 1 |
6 |
||||
|
|
|
|
||||
Уравнение (6.6) является нелинейным относительно p и q , точное решение которого достаточно трудоемко. С достаточной для практики точностью уравнение может быть линеаризовано условием
|
|
pq |
1, или pq p q 1, |
(6.7) |
|
|
|
|
|
||
|
|
|
|
||
|
|
p q 1 |
|||
|
|
|
|
||
при котором уравнение (6.6) принимает вид |
|
||||
|
|
|
|
p q 6 . |
(6.8) |
Подставляя равенство (6.8) в (6.2) – (6.4), получим выражения для числовых характеристик времени выполнения работы:
|
t |
|
|
t |
|
|
t |
|
|
t |
|
|
|
p |
; |
|
(6.9) |
||||
|
ож |
min |
max |
min |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t |
|
|
t |
|
|
|
t |
|
|
t |
|
|
|
p 1 |
; |
(6.10) |
|||||
н.в |
min |
max |
min |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
tmax |
tmin |
|
(сравни с (6.5)). |
(6.11) |
||||||||||||||
t |
|
6 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из уравнений (6.9) и (6.10) возможно получить зависимость математического ожидания времени выполнения работы от наиболее вероятного времени выполнения работы
t |
|
|
tmin |
4tн.в tmax |
. |
(6.12) |
ож |
|
6 |
||||
|
|
|
|
|
||
|
|
|
|
|
|
Чаще всего определение tmin и tmax методом экспертных оценок не вызывает затруднений, тогда как определение tн.в производится с большой погрешностью. Поэтому целесообразно использовать такую методику, которая позволила бы производить оценку tож при наличии информации о граничных значениях времени выполнения работы.
120
Анализ эмпирических данных показал, что параметры распределения группируются около значений p 2 и q 3. Для такого распределения из формул (6.3) и (6.4) имеем:
t |
|
|
|
3tmin |
2tmax |
; |
(6.13) |
||
ож |
|
|
|
6 |
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tmax |
tmin |
. |
(6.14) |
||
|
t |
|
5 |
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Следует отметить, что последние оценки можно использовать для работ таких процессов, для которых характерны налаженное материальное обеспечение, высококвалифицированный персонал и отсутствие «текучки» кадров.
Для процессов, которые характеризуются перебоями в материальном обеспечении, нехваткой специалистов и их низкой квалификацией, следует пользоваться распределениями, у которых вершина распределения сдвинута вправо.
Бета-распределение, естественно, не является единственным распределением, отражающим особенности выполнения различных работ, в частности, могут использоваться треугольное, логарифмически-нормальное, усеченное нормальное.
Ранний срок наступления события. Событие может наступить только тогда, когда будут выполнены все работы всех путей от исходного события к данному. Следовательно, оно не может наступить раньше окончания работ, принадлежащих самому длинному из путей. Ранний срок наступления события численно равен продолжительности выполнения всей
последовательности работ самого длинного пути, а именно |
||
|
t p ( j) max t p (i) tij , |
(6.15) |
|
i G |
|
где |
G – множество индексов событий, предшествующих |
|
событию j; |
|
|
tp(i), tp(j) – ранние сроки наступления i-го и j -го событий;
t(i,j) – продолжительность работы, начальный индекс которой равен i, а конечный – j.
Ранний срок наступления первого события tp(6.78) принимается равным нулю, или календарному сроку начала работ. Тогда формулой (6.15) можно воспользоваться как рекур-
121
рентной19 для определения ранних сроков наступления всех событий сетевого графика:
t p (1) 0 (по определению);
t p (2) t p (1) t12 0 0,5 0,5 ч;
t p (3) t p (1) t13 |
0 2,0 2,0 ч; |
|
||||||
t p |
t |
p |
(2) t |
24 |
0,5 1,0 1,5 |
|||
(4) max |
|
|
|
|
1,5 ч; |
|||
|
|
t p (1) t21 0 1,0 1,0 |
|
|||||
t p |
t |
p |
(4) t |
45 |
1,5 0 1,5 |
4,0 ч; |
||
(5) max |
|
|
|
|
||||
|
t p (1) t15 0 4,0 4,0 |
|
||||||
t p (6) t p (5) t56 |
4,0 0,5 4,5 ч; |
|
||||||
t p |
t |
p |
(4) t |
47 |
1,5 1,5 3,0 |
|||
(7) max |
|
|
|
|
4,5 ч; |
|||
|
t p (6) t67 |
4,5 0 4,5 |
|
|||||
|
t |
p |
(6) t |
68 |
4,5 0 4,5 |
|||
t p |
(8) max |
|
|
4,5 ч; |
||||
|
t p (3) t38 |
4,5 0 4,5 |
||||||
t p |
t |
p |
(7) t |
79 |
4,5 1,0 5,5 |
|||
(9) max |
|
|
|
|
6,5 ч; |
|||
|
t p (8) t89 |
4,5 2,0 6,5 |
||||||
t p |
t |
p |
(9) |
t |
910 |
6,5 3,0 9,5 |
6,5 ч; |
|
(10) max |
|
|
|
|
||||
|
t p (3) |
t310 |
2,0 1,0 3,0 |
|
|
|||
t p (11) t p (10) t1011 9,5 2,0 11,5 ч.
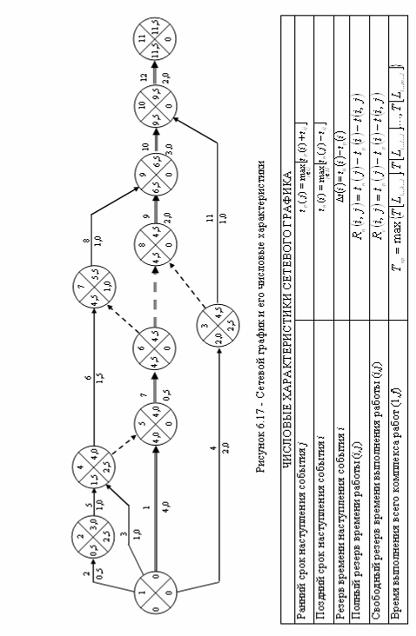
С целью дальнейшей разработки сетевого графика произведена детализация обозначения событий: кружокобозначение события разделен на четыре сектора. В верхние секторы обозначений событий внесены их номера, в левые секторы - полученные значения ранних сроков наступления событий (рисунок 6.17).
Поздний срок наступления события. Если ранний срок наступления события утверждает, что некоторое событие i не может наступить раньше окончания работ, принадлежащих самому длинному пути от исходного события к данному, то возникает вопрос: допустимо ли его наступления позже
19 Рекуррентной формулой называется формула, позволяющая вычислять все члены последовательности, если заданы несколько первых членов.
122
этого срока? Допустимо, если более позднее наступления события i не помешает своевременному окончанию всего комплекса работ. Это возможно в том случае, когда путь максимальной продолжительности от события i до завершающего f
меньше разности Тз - tp(i), т.е. max T L i, f Tз t p i .
L i, f
123
Следовательно, поздний срок наступления события
можно определить по формуле |
|
tп i tр i t i , |
(6.16) |
|
|
|
124 |
|
где комплекс |
i Tз |
|
i max T L i, f |
|
t |
tр |
(6.17) |
||
|
|
|
L i, f |
|
- резерв времени наступления события, показываю-
щий на какой предельный срок можно задерживать наступление события i.
После преобразований формул (6.16) и (6.17) возможно получить рекуррентную формулу для позднего срока наступ-
ления события |
(i) max t |
|
, |
|
tп |
п ( j) tij |
(6.18) |
||
|
j H |
|
|
|
где Н – множество индексов j, непосредственно следующих за i. При известном позднем сроке наступления завершающего события tп(f) формула (6.18) позволяет последовательно
определить поздние сроки наступления всех событий сетевого
графика. Логично положить |
|
|
tр f tп |
f Tз , |
(6.19) |
где Тз - заданный (директивный) срок выполнения всего комплекса работ (процесса).
Для поздних сроков наступления всех событий исследу-
емого сетевого графика имеем: |
|
|
|||||||
tп (11) t р (11) |
Т з 11,5 ч; |
|
|
||||||
tп (10) tп (11) t1011 11,5 2,0 9,5 ч; |
|
||||||||
tп (9) tп (10) t910 9,5 3,0 6,5 ч; |
|
|
|||||||
tп (8) tп (9) t89 |
6,5 2,0 4,5 ч; |
|
|
||||||
tп (7) tп (9) t79 |
6,5 1,0 5,5 ч; |
|
|
||||||
tп |
t |
(7) t |
|
|
5,5 0 5,5 |
4,5 ч; |
|||
(6) min п |
|
|
|
67 |
|
||||
|
tп (8) t68 |
4,5 0 4,5 |
|
|
|||||
tп (5) tп (6) t56 |
4,5 0,5 4,0 ч; |
|
|
||||||
tп |
t |
(7) t |
|
|
5,5 1,5 4,0 |
4,0 ч; |
|||
(4) min п |
|
|
|
47 |
|
|
|||
|
tп (5) t45 |
4,0 0 4,0 |
|
|
|||||
tп |
t |
п |
(8) t |
38 |
4,5 0 4,5 |
|
4,5 ч; |
||
(3) min |
|
|
|
|
|
||||
|
tп |
(9) t310 |
9,5 1,0 8,5 |
|
|||||
tп (2) tп (4) t24 |
4,0 1,0 3,0 ч; |
|
|
||||||
|
|
|
|
125 |
|
|
|
|
|
t |
п (2) t12 |
3,0 |
0,5 |
2,5 |
|
||
|
|
|
(4) t14 |
4,0 1,0 3,0 |
|
|
||
tп |
t |
п |
|
0 . |
||||
(1) min |
|
(5) t15 |
4,0 4,0 0 |
|
||||
|
tп |
|
|
|||||
|
t |
|
(3) t |
4,5 |
4,0 |
0,5 |
|
|
|
п |
13 |
|
|
|
|
|
|
Отметим, что поздний срок наступления первого события при условии (6.19) всегда равен нулю.
Внесем полученные значения поздних сроков наступления событий в правые секторы обозначений событий (рисунок 6.17).
Резерв времени наступления события, как следует из
формулы (6.16), определяется |
|
|
|
||||
|
|
|
|
t i tп |
i tр i . |
(6.20) |
|
Резервы времени наступления событий сетевого графи- |
|||||||
ка равны: |
|
|
|
|
|
|
|
t(6.78) = 0 – |
0 |
= 0; |
t(6.44) = 5,5 – 4,5 = 1,0 ч; |
||||
t(6.79) = 3,0 |
– 0,5 = 2,5 ч; |
t(6.45) |
= 4,5 – 4,5 = 0; |
|
|||
t(6.40) |
= 4,5 |
– 2,0 |
= 2,5 ч; |
t(6.46) |
= 6,5 – 6,5 = 0; |
|
|
t(6.41) |
= 4,0 |
– 1,5 |
= 2,5 ч; |
t(6.47) |
= 9,5 – 9,5 = 0; |
|
|
t(6.42) |
= 4,0 |
– 4,0 |
= 0; |
t(6.48) |
= 11,5 – 11,5 = 0; |
|
|
t(6.43) |
= 4,5 |
– 4,5 |
= 0; |
|
|
|
|
Для исследуемого сетевого графика значения резервов времени наступления событий внесены в нижние секторы обозначений событий.
Полный резерв времени выполнения работы вычисля-
ется по формуле |
i, j tп j t р |
i t i, j . |
|
Rп |
(6.21) |
Полный резерв времени показывает, насколько можно увеличить продолжительность отдельной работы или перенести ее начало без изменения времени выполнения всего комплекса работ.
Полные резервы времени для всех действительных ра-
бот соответственно равны: |
|
|
|
|
|||
Rп(1,2) = 3,0 – 0 – |
0,5 |
= 2,5 ч; |
Rп(4,7) = 5,5 – 1,5 – |
1,5 = 2,5 ч; |
|||
Rп(1,3) = 4,5 |
– 0 – |
2,0 |
= 2,5 ч; |
Rп(5,6) = 4,5 – 4,0 – 0,5 = 0; |
|||
Rп(1,4) = 4,0 |
– 0 – |
1,0 |
= 3,0 ч; |
Rп(7,9) = 6,5 – 4,5 – |
1,0 = 1,0 ч; |
||
Rп(1,5) = 4,0 |
– 0 – |
4,0 |
= 0; |
Rп(8,9) = 6,5 – 4,5 – 2,0 = 0; |
|||
Rп(2,4) = 4,0 |
– 0,5 |
– 1,0 = 2,5 ч; |
Rп(9,10) = 9,5 – |
6,5 |
– |
3,0 = 0; |
|
Rп(3,10) = 9,5 – 2,0 – 1,0 = 6,5 ч; Rп(10,11) = 11,5 |
– 9,5 |
– 2,0 = 0. |
|||||
126
Если полный резерв времени выполнения одной из работ использовать полностью, то аннулируются полные резервы времени выполнения других работ, лежащих на данном пути. Например, при полном использовании резерва времени работы (2,4) события 4 и 7 наступят в свои поздние сроки, и работы (4,7) и (7,9) не будут иметь резервов.
В связи с этим исполнитель отдельной работы не может распоряжаться полным резервом времени выполняемой им работы, так как его использование приведет к сокращению или полной ликвидации резервов других исполнителей. Полный резерв времени выполнения каждой работы находится в распоряжении руководителя всего комплекса работ.
Свободный резерв времени выполнения работы вы-
числяется по формуле |
|
|
|
Rс i, j t р |
j t р |
i t i, j . |
(6.22) |
Свободный резерв времени выполнения работы показывает, насколько можно увеличить время выполнения отдельной работы или отложить ее начало, не изменяя ранних сроков начала последующих работ.
Свободные резервы времени для всех действительных
работ соответственно равны: |
|
|
|
|
|
|||||
Rс(1,2) = 0,5 |
– 0 |
– |
0,5 |
= 0; |
Rс(4,7) = 4,5 – |
1,5 |
– |
1,5 |
= 1,5 ч; |
|
Rс(1,3) |
= 2,0 |
– 0 |
– |
2,0 |
= 0; |
Rс(5,6) = 4,5 – |
4,0 |
– |
0,5 |
= 0; |
Rс(1,4) |
= 1,5 |
– 0 |
– |
1,0 |
= 0,5 ч; |
Rс(7,9) = 6,5 – |
4,5 – 1,0 |
= 1,0 ч; |
||
Rс(1,5) |
= 4,0 |
– 0 |
– |
4,0 |
= 0; |
Rс(8,9) = 6,5 – |
4,5 |
– |
2,0 |
= 0; |
Rс(2,4) |
= 1,5 |
– 0,5 |
– 1,0 = 0; |
Rс(9,10) = 9,5 |
– 6,5 |
– 3,0 = 0; |
||||
Rс(3,10) = 9,5 – 2,0 – 1,0 = 6,5 ч; Rс(10,11) = 11,5 – 9,5 – 2,0 = 0.
Использование свободного резерва времени выполнения какой-либо работы не изменяет величины аналогичных резервов следующих за ней работ. Следовательно, свободный резерв времени выполнения работы может находиться в распоряжении исполнителя этой работы.
Время выполнения всего комплекса работ определяет-
ся длиной самого длинного пути от исходного до завершающего события, т.е. длиной критического пути. В общем случае длина критического пути определяется по формуле
Т кр max T L1 k l ,T L1 l l ,...,T L1 m l . (6.23)
Так как полных путей может быть значительное количество, например, для исследуемого сетевого графика их десять:
127
L124791011, L12456791011, …, L131011, то определение критического
пути по формуле (6.23) может быть весьма трудоемким. Признаками работ, лежащих на критическом пути, и са-
мого критического пути являются равенства нулю всех резервов времени: полного и свободного резервов выполнения работы, а также резерва времени наступления события.
Для исследуемого сетевого графика критический путь
Lкр = L156891011, длина которого равна
Ткр = Т[Lкр] = t15+t56+t68+t89+t910+t1011 = 4,0 + 0,5 + 0,0 + 2,0
+ 3,0 + 2,0 = 11,5 ч.
Критический путь на графике выделяется утолщенной или двойной линией.
Увеличение времени выполнения любой работы, лежащей на критическом пути, приведет к увеличению времени выполнения всего комплекса работ. Следует отметить, что критических путей может быть несколько.
Вероятность наступления завершающего события к заданному (директивному) сроку. Предположим, что время выполнения всего комплекса работ Т является случайной величиной, подчиненной нормальному закону распределения. Такое предположение справедливо в том случае, когда длина критического пути Ткр является суммой независимых продолжительностей большого числа работ этого пути, каждая из которых в одинаковой мере мала по сравнению с Ткр. В соответствии с центральной предельной теоремой закон распределения суммы таких случайных величин будет нормальным независимо от законов распределения самих случайных величин.
Математическое ожидание времени выполнения комплекса работ равно сумме математических ожиданий времени выполнения работ, принадлежащих критическому пути, т.е.
равно раннему сроку наступления завершающего события f, т.е. |
||
Tож M t p f |
tож |
i, j ; |
|
i, j Lкр |
|
а среднеквадратическое отклонение времени выполнения комплекса работ определяется формулой
|
|
|
, |
T |
|
t2 i, j |
|
|
|
i, j Lкр |
|
где Lкр – множество работ, принадлежащих критическому пути;
128
М[] – символ математического ожидания.
Для нормального закона распределения времени выполнения всего комплекса работ:
директивное время должно находится в пределах
Тож - 3Т < Тз < Тож + 3Т;
вероятность наступления завершающего события f в заданный срок Тз
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
Tз Т ож 3 Т ; |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
Т з |
Т ож |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; (6.24) |
|||||||||||
р |
з |
з |
|
Ф |
|
|
|
|
|
,Т |
ож |
3 |
Т |
T |
з |
Т |
ож |
3 |
Т |
|||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Т |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
|
T |
з |
Т |
ож |
3 |
Т |
, |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где Ф t |
|
1 |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
e t 2 / 2 dt |
– функция Лапласа. |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как функция нечетная, т.е. Ф(-t) = -Ф(t), то ее можно |
||||||||||||||||||||||||||||||||
|
|
Ф t |
|
|
|
2 |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
записать |
|
|
|
|
|
e t 2 / 2 dt . |
Значения функции |
|
Лапласа |
|||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
которой табулированы и приведены в руководствах по теории вероятностей.
Для работ, принадлежащих критическому пути исследуемого сетевого графика, методом экспертных оценок определены минимальные и максимальные значения tmin и tmax, остальные оценки получены для бета-распределения с р = 2 и q = 3 и сведены в таблицу 6.3.
Таблица 6.3 – Числовые характеристики работ критического пути
Обозначение |
tmin |
tmax |
tож |
tн.в |
t |
|
работы |
(ф. (6.13)) |
(ф. (6.10)) |
(ф. (6.14)) |
|||
|
|
|||||
(1,5) |
3,40 |
4,90 |
4,00 |
3,78 |
0,30 |
|
(5,6) |
0,43 |
0,61 |
0,50 |
0,47 |
0,04 |
|
(8,9) |
1,70 |
2,45 |
2,00 |
1,89 |
0,15 |
|
(9,10) |
2,55 |
3,68 |
3,00 |
2,83 |
0,23 |
|
(10,12) |
1,70 |
2,45 |
2,00 |
1,89 |
0,15 |
Числовые характеристики времени выполнения всего комплекса работ равны:
математическое ожидание
Тож = 4,0 + 0,5 + 2,0 + 3,0 + 2,0 = 11,5 ч;
среднеквадратическое отклонение