138

Рассмотрены два вида сетевых моделей: сетевая мо-

дель по методу критического пути (Critikal Path method –

сети CPM), в которой реализован детерминированный подход к заданию длительности работ; сетевая модель по методу анализа и оценки программ (Program Evaluation and Review Technique – сети PERT), в которой реализован стохастический подход к заданию длительности работ.

Наряду с этими сетевыми моделями широкое распространение получили метод сетей предшествования, метод анализа и графической оценки (сети GERT), сети Петри, рассмот-

ренные в [3.2, 3.6, 3.9, 3.10].

6.2 Управление эксплуатацией вооружения КВ с использованием методов математического программирования

6.2.1 Основные понятия и определения линейного программирования

Методы математического программирования используются для поиска экстремального (максимального или минимального) значения функции при накладываемых ограничениях на нее или ее параметры (либо на то и другое одновременно). Оптимизируемая функция не зависит от времени, количества параметров целевой функции, как правило, больше одного, алгоритмы вычислений в методах математического программирования ориентированы на использование вычисли-

тельной техники [3.2, 3.6, 3.9, 3.10].

Чаще всего используются следующие методы математического программирования: линейное, нелинейное, динамическое, целочисленное, стохастическое. Выбор метода определяется видом оптимизируемой функции и накладываемых ограничений. В Учебном пособии рассмотрен метод линейного программирования.

Линейное программирование (планирование) – математический метод отыскания максимума или минимума линей-

ной функции (целевой функции) при наличии ограничений в

виде линейных неравенств или уравнений. Ограничения характеризуют имеющиеся возможности решения задачи.

Максимизируемая (минимизируемая) целевая функция представляет собой принятый критерий эффективности решения задачи, соответствующий поставленной цели.

139

Сущность решения задач линейного программирования заключается в том, чтобы найти условия, обращающие целевую функцию в максимум или минимум. Решение, удовлетворяющее условиям задачи и соответствующее намеченной це-

ли, называется оптимальным планом.

Линейное программирование служит для выбора наилучшего плана распределения ограниченных ресурсов в целях решения поставленной задачи. Под ресурсами понимаются имеющиеся в наличии силы, средства, запасы.

Любую задачу линейного программирования можно свести к стандартной форме, так называемой «основной задаче линейного программирования» (ОЗЛП), которая формулируется следующим образом: найти неотрицательные значения переменных х1, х2,…, хn, которые удовлетворяли бы условиямравенствам

где aij и bi – известные постоянные величины, характеризующие условия задачи, и обращали бы в максимум линейную целевую функцию этих переменных

где cj – постоянные коэффициенты (коэффициенты стоимости). Случай, когда целевую функцию надо обратить в мини-

мум, сводится к предыдущей форме записи, если поменять знак у на противоположный (максимизировать не у, а - y’= -y).

От любых условий-неравенств можно перейти к услови- ям-равенствам путем введения новых «дополнительных» переменных. Покажем этот переход на конкретном примере.

Пусть требуется найти неотрицательные значения переменных х1, х2, х3, удовлетворяющие ограничениямнеравенствам

140

3x1 2x2 x3 4, x1 2x2 3x3 10

и обращающие в максимум целевую функцию y 4x1 x2 2x3 max .

Приведем ограничения-неравенства к стандартным условиям, так, чтобы знак неравенства был ≥, а справа стоял 0. Получим

3x1 2x2 x3 4 0,

x1 2x2 3x3 10 0.

Обозначим левые части последних неравенств соответственно через новые «дополнительные» переменные х4, х5

x4 3x1 2x2 x3 4, x5 x1 2x2 3x3 10.

Новые переменные также неотрицательны.

Задача формулируется следующим образом: найти неотрицательные значения переменных х1, х2, х3, х4, х5 такие, чтобы они удовлетворяли условиям-равенствам и обращали в максимум целевую функцию

y 4x1 x2 2x3 0x4 0x5 max .

Известно, что m линейно независимых уравнений всегда можно разрешить относительно m базисных переменных, выразив их через остальные, свободные, число которых равно k = n – m. Если число свободных переменных k = 2, то решение задачи имеет геометрическую интерпретацию.

Приведем несколько задач линейного программирования.

6.2.2 Задача распределения оружия по носителям

Постановка задачи. Пусть m – число различных типов оружия (ракет, снарядов и т.п.), а n - число носителей этого оружия (кораблей, самолетов и т.п.). Известно количество

единиц оружия i – го типа ( i 1, m ) на j - м носителе aij ( j 1, n ), а также общее число оружия i – го типа bi для сна-

ряжения им вех носителей. Известно ожидаемое противодействие противника: cj – вероятность поражения j - го носителя.

Формализация задачи. Оптимальным образом распределить оружие по носителям, т.е. найти требуемое количество

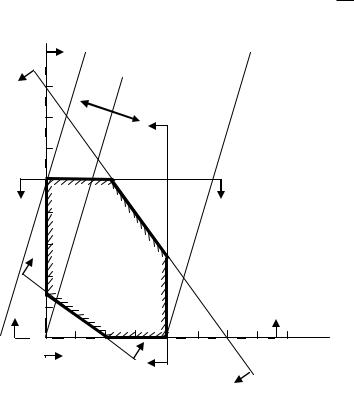
143

неравенствам значения переменных величин x j j 1, n (ри-

сунок 6.26).

а) схема построения области допустимых планов

б) оптимальный план распределения оружия по носителям

Рисунок 6.26 – Схема построения области допустимых планов и оптимальный план распределения оружия по носителям

144

На координатной плоскости 0x1x2 неравенству x1 ≥ 0 соответствует полуплоскость вправо от оси 0x2; неравенству x2 ≥ 0 - полуплоскость вверх от оси 0x1.

Неравенству x3 8x1 12x2 16 0 соответствует по-

луплоскость вправо и вверх от линии, соответствующей граничному значению данного неравенства (при x3 = 0). Уравне-

ние этой линии x1 32 x2 2 0 . Таким же образом можно построить границы, определяемые другими неравенствами: (x4

= 0) – x1 = 4; (x5 = 0) – x2 = 5; (x6 = 0) - x1 34 x2 6 0.

Направления на полуплоскости, на которых выполняются неравенства (6.31), указаны на рисунке стрелками.

Как следует из рисунка, неравенствам (6.31) соответствует некоторая область, образованная границами упомянутых выше полуплоскостей. Эта область называется областью допустимых планов, поскольку любая точка в ее пределах отвечает требованиям системы уравнений (6.27). Из всех допустимых планов интерес представляет оптимальный план, при котором целевая функция достигает минимума.

Целевой функции соответствует семейство параллельных прямых. Рассмотрим одну из них, проходящую через начало координат: т.к. x1 = 0 и x2 = 0, то из (6.30) следует, что у = 22,8. Уравнение этой линии в системе координат 0x1x2 может быть получено в результате подстановки в уравнение целевой функции (6.30) ее значения у = 22,8, т.е. 22,8 2,4x1 0,8x2 22,8. Следовательно, x2 = 3 x1. Пере-

мещая данную прямую параллельно самой себе, получим семейство прямых, удовлетворяющих неравенствам (6.31). Целевая функция будет иметь максимальное значение ymax = 26,8

при x1 = 0 и x2 = 5; минимальное - ymin = 13,2 при x1 = 4 и x2 = 0. Так как по условиям задачи требуется минимум целевой

функции ymin = 13,2, то оптимальный план будет следующим:

x1 = 4; x2 = 0; x3 = 16; x4 = 0; x5 = 10; x6 = 8.

Выводы:

1 Оптимальное решение достигается в одной из вершин области допустимых планов, в опорной точке, где, по крайней мере, k = 2 переменных равны нулю.