145

3 Для обеспечения минимальных потерь необходимы 4 носителя 1-го; 16 – 3-го; 10 – 5-го; 8 – 6-го типов. Потери при этом составят 13,2 единиц, в том числе: 1,6 – 1-го; 3,2 - 3-го; 6

–5-го; 2,4 – 6 – го типов.

6.2.3Транспортная задача линейного программирования

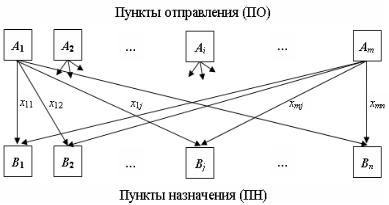
Транспортная задача ставится следующим образом: имеются m пунктов отправления (ПО) A1, A2,…, Am, в которых сосредоточены запасы однородных грузов в количестве a1, a2,…, am соответственно (рисунок 6.27). Имеется n пунктов назначения (ПН) B1, B2,…, Bn, подавших заявки соответственно на b1, b2,…, bn единиц груза.

Рисунок 6.27 – Схема транспортной задачи

Сумма всех заявок равна сумме всех запасов

Известны стоимости cij перевозки единицы груза от каждого ПО Ai до каждого ПН Bj (i = 1, 2, …, m, j = 1, 2, …, n), которые образуют матрицу

149

В таблице 6.6 проставляются только отличные от нуля перевозки, клетки, соответствующие нулевым перевозкам, оставляем свободными. Проверим, является ли план перевозок опорным. Число свободных клеток с нулевыми перевозками равно 12. Так как (m - 1) (n - 1) = 3 . 4 =12, то план является опорным.

Однако план не является оптимальным, так как стоимость перевозок вообще не учитывалась при составлении плана перевозок. Из анализа плана следует, что его можно улучшить, если произвести перестановку перевозок между клетками таблицы. Например, уменьшить перевозки в «дорогой» клетке (2, 3) со стоимостью 12, но увеличить перевозки в «дешевой» клетке (2, 4) со стоимостью 6. Чтобы план оставался опорным, необходимо одну из свободных клеток (например, (2, 4)) сделать базисной, а одну из базисных – свободной (напри-

мер, (3, 4)). Из анализа цикла (2, 4) → (3, 4) → (3, 3) → (2, 3)

следует, что можно увеличить перевозки в четных и уменьшить в нечетных вершинах цикла не более чем на 11 единиц, иначе перевозки в клетке (3, 4) станут отрицательными.

Общая стоимость перевозок допустимого плана перево-

зок у1 = 18 . 13 + 12 . 7 +15 . 8 + 33 . 12 + 9 . 10 + 11 . 8 + 4 . 10 +

26 . 15 = 1442; общая стоимость улучшенного плана у2 = 18 . 13 + 12 . 7 +15 . 8 + 22 . 12 + 11 . 6 + 20 . 10 + 4 . 10 + 26 . 15 = 1398.

Следовательно, уменьшение стоимости перевозок составило 44 единицы. Пример улучшенного плана представлен таблице 6.7.

Таблица 6.7 - Пример улучшенного плана

Принято, что считать стоимость в вершине цикла со знаком плюс, если перевозки в ней увеличиваются, и со зна-

150

ком минус, если перевозки уменьшаются. Алгебраическая сумма стоимостей в вершинах цикла называется ценой цикла. Если она отрицательная, то возможно уменьшение стоимости перевозок. Для исследуемого цикла его цена равна 6 – 8 + 10 – 12 = - 4, т.е. при переносе одной единицы груза стоимость перевозок уменьшается на 4 единицы. Сущность оптимизации плана перевозок заключается в том, чтобы переносить перевозки по циклам, имеющим отрицательную цену.

В теории линейного программирования доказывается, что при опорном плане для каждой свободной клетки транспортной таблицы существует цикл, и притом единственный, одна вершина которого лежит в данной свободной клетке, а остальные в базисных клетках.

Продолжая анализ улучшенного плана, для свободной клетки (1, 5) цикл будет состоять из последовательности кле-

ток: (1, 5) → (4, 5) → (4, 4) → (2, 4) → (2, 2) → (1, 2) → (1, 5).

Цена 5 – 15 + 10 – 6 + 8 – 7 = - 5. Так как цена цикла отрицательна, то переброска по этому циклу приведет к снижению стоимости. Максимальный размер (объем) перемещаемой перевозки определяется наименьшей перевозкой, стоящей в отрицательной вершине цикла. В данном случае 11 единиц (клетка (2, 4)). Следовательно, за счет переброски перевозок по данному циклу можно достичь снижения стоимости на 5 . 11 = 55 единиц. Вид оптимального плана перевозок после этой перевозки представлен таблице 6.8.

Таблица 6.8 - Оптимальный план

В теории линейного программирования существуют способы, позволяющие автоматически, без поисков и раз-