207

ным анализом однофакторного комплекса:

индекс i; B6 – F9 – значения результативного признака xij; G6 – G9 – средние арифметические выборок xi*; G10 – общая средняя всех совокупностей x ; H6 – H9 – значения квадратов xi* x 2 ; B11 – F14 – значения квадратов xij xi* 2 ; G11 – G14 – суммы

квадратов 5 xij xi* 2 ; B16 – B19 – суммы Q1, Q2, Q; D16 – D19 – оценки дисперсий;

j 1

F16 – F19 – степени свободы; B19 – значение уровня значимости ; B20 – расчетное значение показателя F; D20 – теоретическое (табличное) значение показателя F ; B21 – результат проверки гипотезы по F – критерию.

6.7.3 Двухфакторный комплекс

Если исследуется действие двух факторов, например, оценить показатели качества материала, находящегося на хранении в различных условиях (фактор А) после транспортирования различными видами транспорта (фактор В). Для простоты рассмотрим случай, когда для каждого хранилища и каждого вида транспорта имеется одно наблюдение результативного признака. Тогда матрица наблюдений может быть записана в виде таблицы 6.25.

Таблица 6.25 - Матрица наблюдений двухфакторного комплекса

Если имеется r хранилищ, то в матрице наблюдений им соответствует r строк, которые называются уровнями фактора А. Если имеется v видов транспорта, то им соответствует v столбцов, которые называются уровнями фактора В.

Пересечение i-го и j-го уровней образует ij-ю ячейку, в которую записываются наблюдения, полученные при одновременном исследовании факторов А и В на i-м и j-м уровнях соответственно.

По каждому строке и столбцу вычисляются средние значения, а также общее среднее:

208

Основное тождество дисперсионного анализа в данном случае имеет вид30

Слагаемое Q1 представляет собой сумму квадратов разностей между средними по строкам и общим средним и характеризует изменение результативного признака по фактору А. Слагаемое Q2 представляет собой сумму квадратов разностей между средними по столбцам и общим средним и характеризует изменение результативного признака по фактору В. Слагаемое Q3 называется остаточной суммой квадратов и характеризует влияние неучтенных факторов. Сумма Q называется общей или полной суммой квадратов отклонений отдельных наблюдений от общей средней.

Оценка дисперсий определяются по формулам:оценка полной (общей) дисперсии

В двухфакторном анализе для выяснения значимости влияния факторов А и В на результативный признак сравни-

30 При преобразовании тождества (6.143) к выражению в скобках прибавили и отняли xi* , x* j и x .

210

дисперсионный анализ. Естественно в этих моделях дисперсионного анализа существенно усложняются вычисления, но их сущность остается прежней.

211

6.8 Особенности применения корреляционнорегрессионого анализа

Знание статистической зависимости между случайными величинами, характеризующими явление (процесс, событие), имеет большое практическое значение в эксплуатации вооружения КВ: с ее помощью можно прогнозировать значение зависимой случайной величины в предположении, что независимая величина примет определенное значение.

Известно, что дисперсионный анализ позволяет установить влияние тех или иных факторов на рассматриваемый результативный признак, но он не дает возможности определить ни степени этого влияния (тесноту связи), ни формы этого влияния. При решении этих вопросов на помощь исследователю приходит корреляционно-регрессионный анализ, позволяющий измерить тесноту связи, ее направление и форму.

Если в дисперсионном анализе факторные признаки описываются качественно, а результативный признак – количественно, то в корреляционно-регрессионном анализе и факторные и результативный признаки описываются только количественно, т.е. они должны быть измерены.

6.8.1 Задачи и предпосылки корреляционнорегрессионного анализа

В процессе статистического исследования объективно существующих связей между явлениями вскрываются при- чинно-следственные отношения между ними. Явление (процесс, событие) называется причиной другого явления (процесса, события), если выполняются два условия: 1) первое явление предшествует второму по времени; 2) первое явление является необходимым условием, предпосылкой или основой возникновения, изменения или развития второго, иными словами, первое порождает второе. Второе явление является следствием первого. Следовательно, причинно-следственные отношения – это такая связь явлений (процессов, событий), когда изменение одного из них – причины – ведет к изменению другого - следствия.

Особое значение при исследовании причинноследственных связей имеет выявление временной последовательности: причина всегда предшествует следствию, однако

212

не всякое предшествующее событие является причиной, а последующее – следствием.

Между группами причин и следствий возможны многозначные связи, когда за одной причиной будет следовать не одно, а несколько следствий, или одно следствие будет иметь несколько причин. Чтобы установить однозначную причинную связь между явлениями или предсказать возможные следствия конкретной причины, необходима абстракция от всех прочих явлений в исследуемой временной или пространственной области.

Из всего многообразия связей между признаками выделяют функциональную и стохастическую зависимости (связи).

В технике и естествознании, как правило, речь идет о

функциональной зависимости между переменными (величи-

нами) x и y, когда каждому возможному значению x поставлено в однозначное соответствие определенное значение y. Это могут быть, например: в физике - зависимость между давлением р и температурой t газа (закон Шарля); в астрономии – зависимость силы притяжения F от масс взаимодействующих тел m1 и m2, а также - расстояния между телами R (закон тяготения); в гидродинамике– зависимость подъемной силы P от скорости потока v и угла атаки и др.

В реальном мире все явления природы происходят в условиях действия многочисленных факторов, влияние каждого из которых ничтожно, а число их велико. В этих случаях связь теряет свою строгую функциональность и изучаемая система (физическая, техническая, экономическая, социальная и т.п.) переходит не в определенное состояние, а в - одно из возможных для нее состояний. В этом случае речь идет о так называемой стохастической связи, сущность которой состоит в том, что одна случайная величина реагирует на изменение другой изменением своего закона распределения. В общем случае между двумя случайными величинами имеется стохастическая зависимость тогда, когда существуют некоторые случайные факторы, которые влияют на обе случайные величины, и некоторые факторы, действующие только на первую или только на вторую случайную величину. Следовательно,

если X f Z1 ,..., Zm , X1 ,..., X k и Y g Z1 ,..., Zm ,Y1 ,...,Yj , где

Z1,…, Zm – общие случайные факторы, то случайные величины X и Y стохастически зависимы.

где f(y/x) и f(x/y) – условные плотности.

Для случайного вектора (X, Y) выборка объема n дает n

пар значений признака (x1, y1), (x2, y2), …,(xi, yi),…, (xn, yn). Тогда оценки числовых и корреляционных характеристик слу-

чайных величин X и Y:

оценка математических ожиданий x и y

i 1

Корреляционная зависимость между признаками классифицируется по степени тесноты связи, направлению и виду (аналитическому выражению) связи.

Теснота связи характеризует разброс зависимой случайной величины (результативного признака) относительно ее условного математического ожидания и оценивается коэффициентом корреляции при изменении независимой случайной величины (факторного признака). По степени тесноты связи различают: связь практически отсутствует; слабая; уме-

215

ренная и сильная. Количественные оценки тесноты связи приведены в таблице 6.27.

По форме связи различают прямолинейные (или просто линейные) и нелинейные. Форма связи выражается уравнением регрессии.

Таблица 6.27 - Количественные оценки тесноты связи

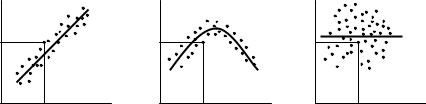
Графически взаимосвязь двух признаков изображается с помощью корреляционного поля (рисунок 6.43). В системе координат на оси абсцисс x откладываются значения факторного признака X, например xi, а на оси ординат – результативного Y, например yi. Каждая пара значений (xi, yi) обозначается на плоскости точкой. Точки группируются вокруг определенной линии, выражающей форму связи (линии регрессии). Если эта линия регрессии представлена прямой (рисунок 6.43, а), то имеет место линейная корреляция, если не является (рисунок 6.43, б), то нелинейная. Если линия (рисунок 6.43, в), параллельна оси абсцисс, то корреляционная связь отсутствует.

Чем сильнее связь между признаками, тем теснее группируются точки вокруг линии, выражающей форму связи.

В прикладных исследованиях используются следующие виды корреляционной зависимости:

парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными);

216

частная корреляция – зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков;

множественная корреляция – зависимость между ре-

зультативным и двумя и более факторными признаками. Корреляционный анализ заключается в количественном

определении тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи). Теснота связи оценивается: при парной корреляции – коэффициентом пар-

ной корреляции; при частной – частными коэффициентами корреляции; при множественной – множественными коэффициентами корреляции (или их квадратами – коэффициентами детерминации).

Для нелинейной связи теснота оценивается корреляционным отношением.

Основной предпосылкой применения корреляционного анализа является необходимость подчинения совокупности значений всех факторных X1, X2,…, Xk и результативного Y признаков k – мерному нормальному закону распределения или близость к нему. Если объем исследуемой совокупности достаточно большой (n > 50), то закон распределения проверяется по критериям Пирсона, Ястремского, Боярского, Колмогорова и др. Если объем совокупности невелик (n < 50), то закон распределения исходной совокупности определяется в результате визуального анализа поля корреляции. Если расположение точек на поле корреляции группируется вокруг прямой линии, то можно предположить, что совокупность исходных данных подчиняется нормальному закону распределения.

Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение зависимой величины или результативного признака обусловлено влиянием одной или нескольких независимых величин или факторных признаков, а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается постоянным.

Для линейно коррелированных случайные величин X и Y

218

По направлению связи различают:

3)прямую (положительную) регрессию (рисунок 6.44,

а), возникающую при условии, если с увеличением или уменьшение факторного признака значения результативного также увеличиваются или уменьшаются;

4)обратную (отрицательную) регрессию (рисунок

6.44, б), возникающую при условии, если с увеличением или уменьшение факторного признака значения результативного соответственно уменьшаются или увеличиваются.

Рисунок 6.44 - Классификация регрессии по направлению связи

Основной предпосылкой регрессионного анализа является то, что только результативный признак имеет нормальный закон распределения, а факторные признаки X1, X2,…, Xk могут иметь произвольный закон распределения.

Одной из проблем построения уравнения регрессии является ее размерность, т.е. определение числа факторных признаков, включаемых в статистическую модель связи.

Сокращение размерности за счет исключения второстепенных, несущественных факторов позволяет быстрее получить статистическую модель связи. В то же время построение модели малой размерности может привести к тому, что она будет недостаточно полно описывать исследуемое явление (процесс, событие).

Теория статистики рекомендует следующее правило «оптимального числа факторов»: число факторов, включенных в модель связи должно быть в 5 – 6 раз меньше числа наблюдений.

Корреляционно-регрессионный анализ как общее поня-

тие включает в себя измерение тесноты, направления связи и установление аналитического выражения (формы) связи.