219

6.8.2 Парная линейная регрессия

Рассмотрим построение статистической модели на примерах парной регрессии, т.е. на объект исследования воздействует факторный признак X, в результате чего изменяется результативный признак Y.

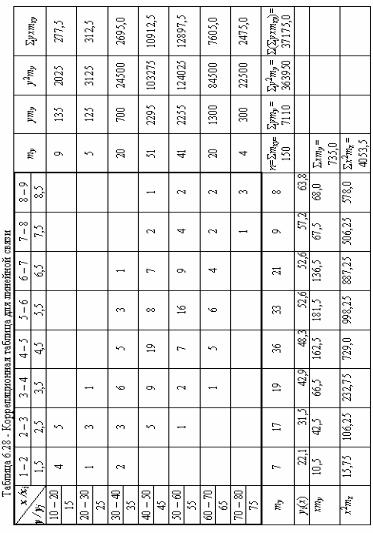
Исходные данные помещены в таблице 6.28. В результате n = 150 наблюдений получено 150 пар случайных чисел (x, y). Задача заполнения упрощается, если выборку упорядочить. Для этого значения x и y разбивают на интервалы. Случайная величина X (факторный признак) изменяется от 1 до 9, ее можно разбить на 8 интервалов: 1 – 2; 2 – 3; …; 8 – 9. Для каждого интервала вычисляется среднее значение xi = 1, 5; 2,5, …, 8,5.

Случайная величина Y (результативный признак) изменяется от 10 до 80, ее можно разбить на 7 интервалов: 10 – 20; 20 – 30; …; 70 – 80. Для каждого интервала вычисляется среднее значение yj = 15; 25, …, 75. Границы интервалов для случайных величин X и Y и их средние значения занесены в таблицу. В ячейки, образованные пересечением строк и столбцов, заносится количество попаданий пар (x, y) в соответствующие интервалы по x и y. Например, в интервал по x от 1 до 2 и интервал по y от 10 до 20 попало 4 пары наблюдавшихся значений. В регрессионном анализе эти числа называются частотами попаданий и обозначаются через mxy. В столбец, обозначенный my, и строку, обозначенную mx, заносятся суммы частот по каждому интервалу y и x соответственно. В результате заполнения получают корреляционную таблицу. Правильность заполнения таблицы контролируется выполнением условия n = mx = my = 150. Из анализа корреляционной таблицы следует, что имеет место прямая регрессия, так как частоты располагаются по диагонали, идущей с верхнего угла в нижний угол таблицы. Корреляционной таблицей удобно пользоваться при вычислении коэффициентов корреляции и уравнения регрессии.

220

221

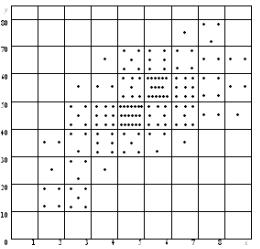
Любую пару случайных чисел (x, y) можно изобразить графически в виде точки с координатами (x; y). По оси абсцисс наносят границы интервалов переменной x, по оси ординат – переменной y (рисунок 6.45). Каждую пару значений (x, y) изображают в виде точки в соответствующей клетке. В результате нанесения всего набора пар случайных чисел получают корреляционное поле случайных величин X и Y.

Рисунок 6.45 - Корреляционное поле случайных величин X и Y

Для каждого интервала x вычисляют среднее значение yi(x), например, для интервала 1 – 2: (15 . 4 + 25 . 1 +35 . 2) / 7 = 22,1. На графике корреляционного поля откладывают для каждого среднего значения интервала x среднее значениям yi(x) для этого интервала.

Соединив точки между собой, получают ломанную ли-

нию, которая называется эмпирической линией регрессии

(рисунок 6.46). По ее виду можно сделать предположение о форме связи. В данном случае эмпирическую линию регрессии можно аппроксимировать прямой линией. Анализ корреляционного поля и эмпирической линии регрессии позволяет сделать вывод о прямой линейной регрессии.

Следует отметить, что линейная регрессия, или линейная форма связи между случайными величинами, обуславливается двумерным нормальным законом распределения случайных переменных X и Y.