
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •1 ИТОГОВАЯ ГОСУДАРСТВЕННАЯ АТТЕСТАЦИЯ ВЫПУСКНИКОВ В СИСТЕМЕ ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
- •1.1 Основные сведения о системе образования
- •1.2 Система высшего и послевузовского профессионального образования
- •1.3 Итоговая государственная аттестация
- •2 ТИПОВАЯ СТРУКТУРА И ТРЕБОВАНИЯ К ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЕ
- •3 ВОЕННО-НАУЧНОЕ ОБОСНОВАНИЕ ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЫ
- •3.1 Место вооружения Космических войск в системе военно-технических средств ВС РФ
- •3.1 Структура военно-научного обоснования темы ВКР
- •3.2 Методика оперативно-тактического обоснования системы вооружения
- •4 ТРЕБОВАНИЯ И РЕКОМЕНДАЦИИ ПО ОФОРМЛЕНИЮ УЧЕБНЫХ ТЕКСТОВЫХ ДОКУМЕНТОВ И ДЕМОНСТРАЦИОННЫХ ПЛАКАТОВ
- •4.1 Назначение и виды учебных текстовых документов
- •4.2 Общие требования к учебным текстовым документам
- •4.3 Титульный и заглавный листы, содержание
- •4.4 Построение документа
- •4.5 Изложение текста
- •4.5.2 Нормативные требования к тексту
- •4.6 Примечания, ссылки, сноски, примеры
- •4.7 Формулы в тексте
- •4.8 Таблицы
- •4.9 Иллюстрации
- •4.10 Приложения
- •4.11 Библиографическое описание произведений печати
- •4.12 Рекомендации по оформлению демонстрационных плакатов
- •5 ПОДГОТОВКА РАСЧЕТОВ И ИХ ВЫПОЛНЕНИЕ
- •5.1 Выбор показателя эффективности
- •5.2 Подготовка исходных данных
- •5.3 Определение точности и надежности оценок
- •5.4 Оценка погрешности расчетов
- •5.5 Запись приближенных чисел
- •5.6 Округление чисел
- •5.7 Предельная погрешность функции
- •5.8 Оценка влияния приращений аргументов на приращение функции
- •6 ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ УПРАВЛЕНИЯ ЭКСПЛУАТАЦИЕЙ ВООРУЖЕНИЯ КВ
- •6.1 Управление процессами эксплуатации вооружения КВ с использованием методов сетевого планирования и управления
- •6.1.1 Основные элементы сетевого графика
- •6.1.2 Правила построения сетевых графиков
- •6.1.3 Характеристики сетевого графика
- •6.1.4 Анализ и оптимизация сетевого графика
- •6.2 Управление эксплуатацией вооружения КВ с использованием методов математического программирования
- •6.2.1 Основные понятия и определения линейного программирования
- •6.2.2 Задача распределения оружия по носителям
- •6.2.3 Транспортная задача линейного программирования
- •6.3 Прогнозирование показателей технического состояния вооружения КВ с использованием временных рядов
- •6.3.1 Прогнозирование: основные понятия и определения
- •6.3.2 Характеристики временного ряда
- •6.3.3 Исследование динамического ряда
- •6.3.4 Прогнозирование показателей технического состояния вооружения КВ
- •6.4 Исследование связи процессов в системе эксплуатации с использованием взаимосвязанных динамических рядов
- •6.4.2 Алгоритм исследования взаимосвязанных динамических рядов
- •6.5 Статистическая оценка показателей эксплуатационных свойств вооружения КВ
- •6.5.1 Выбор закона распределения случайной величины
- •6.5.2 Расчет параметров распределения случайной величины
- •6.5.3 Выравнивание статистического ряда
- •6.5.4 Проверка правдоподобия гипотезы о выборе закона распределения случайной величины
- •6.5.5 Алгоритм статистической оценки показателя эксплуатационного процесса
- •6.6 Метод экспертных оценок показателей эксплуатационных свойств вооружения КВ
- •6.6.1Сущность и содержание метода экспертных оценок
- •6.6.2 Алгоритм применения метода экспертных оценок
- •6.7.1 Общая идея дисперсионного анализа
- •6.7.2 Однофакторный комплекс
- •6.7.3 Двухфакторный комплекс
- •6.8.2 Парная линейная регрессия
- •6.8.3 Парная нелинейная регрессия
- •6.8.4 Множественная регрессия
- •6.8.5 Оценка тесноты связи и значимости коэффициентов регрессии
- •6.9 Прогнозирование состояния системы с использованием марковских процессов и уравнений Колмогорова
- •ЗАКЛЮЧЕНИЕ
- •СПИСОК ЛИТЕРАТУРЫ
- •1. Руководящие и нормативные документы
- •2. Методические материалы
- •3. Дополнительная литература
- •Приложение А
- •Е.1 Основные сведения о Государственной системе стандартизации
- •Е.2 Виды стандартов
- •Е.4 Межотраслевые системы (комплексы) стандартов
- •Е.5 Комплекс стандартов «Государственная система стандартизации РФ»
- •Е.6 Единая система конструкторской документации
- •Е.7 Единая система технологической документации
- •Е.8 Система показателей качества продукции
- •Е.9 Унифицированные системы документации
- •Е.10 Система стандартов по информации, библиотечному и издательскому делу
- •Е.11 Государственная система обеспечения единства измерений
- •Е.12 Единая система защиты от коррозии и старения материалов и изделий
- •Е.13 Комплексы стандартов по безопасности жизнедеятельности
- •Е.14 Система стандартов «Репрография. Микрография»
- •Е.15 Система стандартов «Экологический менеджмент»
- •Е.16 Система разработки и постановки продукции на производство
- •Е.17 Единая система программных документов
- •Е.18 Система проектной документации для строительства
- •Е.19 Обеспечение износостойкости изделий
- •Е.20 Система технической документации на АСУ
- •Е.21 Система стандартов «Расчеты и испытания на прочность»
- •Е.22 Система стандартов «Надежность в технике»
- •Е.23 Система технического обслуживания и ремонта техники
- •Е.24 Система стандартов эргономических требований и эргономического обеспечения
- •Е.25 Комплекс стандартов «Единый российский страховой фонд документации»
- •Е.26 Комплекс стандартов «Информационная технология»
- •Е.27 Система сертификации ГОСТ Р
- •Е.28 Комплекс стандартов «Единообразные предписания …»
- •Е.29 Комплекс государственных стандартов гражданской обороны
- •Е.30 Информационное обеспечение техники и операторской деятельности
- •ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
67
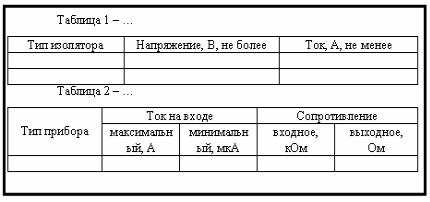
Рисунок 4.14 – Обозначения единиц физической величины в таблице
4.9 Иллюстрации
Иллюстрации (чертежи, схемы, графики, компьютерные распечатки, диаграммы, фотоснимки, эскизы) следует располагать непосредственно после текста, в котором они упоминаются впервые, или на следующей странице. На все иллюстрации должны быть ссылки в документе. Они располагаются в документе так, чтобы их было удобно рассматривать без поворота или с поворотом по часовой стрелке.
Иллюстрации, помещаемые в документе, должны соответствовать требованиям государственных стандартов ЕСКД. Иллюстрации могут быть в компьютерном исполнении, в том числе и цветные.
Иллюстрации обозначаются словом «Рисунок» и нумеруются последовательно арабскими цифрами сквозной нумерацией. Если рисунок один, то он обозначается «Рисунок 1».
Допускается нумеровать иллюстрации в пределах раздела. В этом случае номер иллюстрации состоит из номера раздела и порядкового номера иллюстрации, разделенных точкой, например, Рисунок 1.2 (второй рисунок первого раздела).
При ссылках на иллюстрации следует писать в «соответствии с рисунком 2» при сквозной нумерации и «… в соответствии с рисунком 1.2» при нумерации в пределах раздела.
Иллюстрации при необходимости могут иметь наименование и поясняющие данные (подрисуночный текст или экс-
68
пликацию16), как показано на рисунке 4.15. Слово «Рисунок» и наименование помещают после пояснительных данных и располагают следующим образом: «Рисунок 1 - Детали прибора». Точка в конце наименования рисунка не ставится.
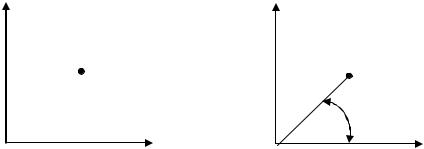
Для иллюстрации функциональных зависимостей нескольких переменных величин выполняются графики, диаграммы, гистограммы, которые дают наглядное представление об этих зависимостях, и, следовательно, облегчают рассмотрение теоретического материала. Графики17 и диаграммы18 могут быть выполнены в декартовой (рисунок 4.16) или в полярной системе координат (рисунок 4.17).
|
|
1 |
|
V |
2 |
|
|
|
ц.м. |
Р |
3 |
|
||
|
|
4 |
р |
|
5 |
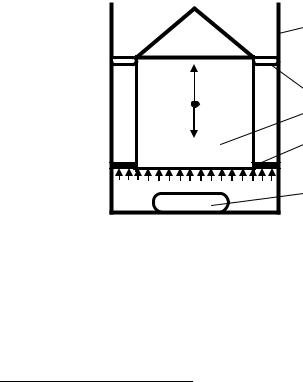
Рисунок 4.15 - Схема минометного старта РН:
1 – транспортно-пусковой контейнер (ТПК); 2 – опорно-ведущий пояс; 3 – РН; 4 – обтюрирующий (уплотняющий) пояс; 5 – пороховой аккумулятор давления (ПАД); ц.м.- центр масс РН; V – скорость; Р - сила тяжести; р – давление, создаваемое ПАД
16Экспликация [лат explicatio - разъяснение] – объяснение условных обозначений, употребляемых на технических рисунках, фотографиях, картах и т.д.
17График [греч. graphikos - начертанный] - чертеж, применяемый для наглядного изображения какой-либо величины от другой.
18Диаграмма [греч. diagramma - рисунок, чертеж] - графическое изображение, наглядно показывающее соотношение между сравниваемыми величинами.
|
|
|
|
|
|
69 |
|
|
|
у |
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
Му |
|
|
|
М(х,у) |
|
|
|
М(ρ,φ) |
|
|
|
|
|
|
|
ρ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ |
||
|
|
|
|
|
|
|
|
|
|
О |
|
|
|
|
х |
О |
|
|
А |
|
|
|
|
|
|
||||
Мх |
|
|
х |
||||||
Рисунок 4.16 – Декартова |
Рисунок 4.17 – Полярная |
||||||||
|
система координат |
|
|
система координат |
|||||
Декартова система координат [по имени французско-
го математика Р. Декарта] – система координат на плоскости или в пространстве с взаимно перпендикулярными осями и одинаковыми масштабами по осям.
Первую ось называют осью абсцисс, вторую – осью ординат, третью (для пространственной системы координат) – осью аппликат, а координаты точки M(x, y, z) - соответственно абсцис-
сой [лат. abscissus - отрезанный]; ординатой [лат. ordinatus -
упорядоченный]; аппликатой [лат. applicata - приложенный].
В прямоугольной системе координат положительные значения величин откладывают на осях, как правило, вправо для независимой переменной и вверх для зависимой переменной от точки начала отсчета.
Полярная система координат на плоскости вводится следующим образом. Выбирают на плоскости какую-нибудь точку О (называют полюсом) и луч ОА (называют полярной осью; обычно берут горизонтальный луч). Выбирают масштаб для измерения длин и положительное направление поворотов вокруг полюса (обычно направление против часовой стрелки). Произвольной точке М на плоскости ставят в соответствие: ρ - расстояние от точки М до полюса О; φ - угол, на который надо повернуть луч ОА до совпадения с лучом ОМ.
Величины ρ и φ называются полярными координатами точки М, ρ - полярным радиусом; φ - полярным углом. В полярной системе координат положительное направление угловых координат должно соответствовать направлению вращения против часовой стрелки.
70
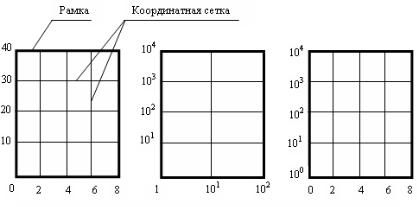
Значения переменных величин откладываются на осях координат в линейном, нелинейном (например, логарифмическом) и смешанном масштабах изображения (рисунок 4.18).
а) |
б) |
в) |
Рисунок 4.18 – Элементы и масштабы изображения:
а – линейный; б – нелинейный (логарифмический); в - смешанный
Диаграммы следует выполнять линиями по ГОСТ 2.303-68. Линии, ограничивающие поле диаграммы, оси координат, оси шкал следует выполнять сплошной основной линией, толщиной S. Примечание – Толщина сплошной основной линии должна быть в пределах от 0,5 до 1,4 мм в зависимости от величины и сложности изображения, а также формата рисунка.
Линии координатной сетки и делительные штрихи выполняют сплошной тонкой линией толщиной S/2. Линию функциональной зависимости выполняют толщиной 2S, но допускается и меньшей толщины, когда необходимо обеспечить высокую точность отсчета.
В качестве шкалы следует использовать координатную ось или линию координатной сетки, которая ограничивает поле диаграммы. Если на одной диаграмме изображены несколько функциональных зависимостей, то допускается проводить дополнительные шкалы параллельно координатным осям.
Координатные оси, шкалы значений изображаемых величин, должны быть разделены на графические интервалы одним из следующих способов:
-координатной сеткой;
-делительными штрихами;
-сочетанием координатной сетки и делительных штрихов.
71
Делительные штрихи, соответствующие кратным графическим интервалам, допускается удлинять.
Числа у шкал следует размещать вне поля диаграммы и располагать горизонтально.
Переменные величины следует указывать одним из следующих способов:
-символом (R, t);
-наименование (сопротивление, время);
-наименованием и символом (R входа, t задержки);
-математическим выражением функциональной зави-
симости ( ddt ).
Единицы измерения следует наносить одним из следующих способов:
-в конце шкалы между последним и предпоследними числами шкалы;
-вместе с наименованием переменной величины после запятой;
-в конце шкалы после последнего числа вместе с обозначением переменной величины в виде дроби, в числителе которой наносят обозначение переменной величины, а в знаменателе – обозначение единицы измерения.
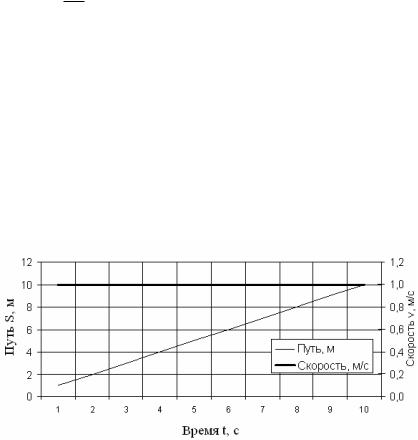
Пример построения графиков с использование табличного процессора Microsoft Excel приведен на рисунке 4.19, а диаграмм – на рисунке 4.20.
Рисунок 4.19 – Пример построения графиков
