
- •Л.В. Коваль, с.О. Скворцова
- •Тема 1. Методика навчання математики в початковій школі як наука та як навчальний предмет.......................................................................................8
- •Передмова
- •Змістовий модуль 1, 2 Загальні питання методики навчання математики в початковій школі теоретичний блок
- •Тема 1. Методика навчання математики в початковій школі як наука та як навчальний предмет
- •Тема 2. Організація навчання математики в початковій школі
- •Питання для самоперевірки
- •Практичний блок
- •Практичне заняття 1
- •Тема. Початковий курс математики як навчальний предмет
- •Основна література
- •Додаткова література
- •Практичні завдання
- •Методичні рекомендації
- •Практичне заняття 2
- •Методичні рекомендації
- •Рефлексія
- •Практичне заняття № 3, 4 Тема. Організація навчання математики в початковій школі План
- •Основна література
- •Додаткова література
- •Практичні завдання
- •Методичні рекомендації
- •Рефлексія
- •Завдання для самостійної роботи
- •Методичні рекомендації для виконання завдань самостійної роботи
- •Змістовий модуль 3, 4 Тема. Сучасні навчальні технології в змісті початкової математичної освіти
- •Теоретичний блок Тема 1. Технологія організації навчальної взаємодії вчителя та учнів
- •Тема 2. Технологія формування загальнонавчальних умінь і навичок молодших школярів
- •Тема 3. Технологія організації диференційованого навчання
- •Тема 4. Технологія організації навчальної проектної діяльності
- •Тема 5. Технологія організації ігрової навчальної діяльності
- •Тема 6. Технологія організації поетапного засвоєння учнями навчального матеріалу
- •Питання для самоперевірки
- •Практичний блок
- •Практичне заняття 1
- •Тема. Новий етап розвитку початкової математичної освіти. Особистісно орієнтований, компетентнісний і технологічний підходи в навчанні математики.
- •Основна література
- •Додаткова література
- •Практичні завдання
- •Практичне заняття 2, 3 Тема. Характеристика сучасних навчальних технологій у системі початкової математичної освіти План
- •Основна література
- •Практичні завдання
- •Практичне заняття 4 Тема. Особливості моделювання та проведення комбінованого уроку математики, побудованого за різними навчальними технологіями План
- •Основна література
- •Додаткова література
- •Практичні завдання
- •Завдання для самостійної роботи
- •Методичні рекомендації до виконання завдань самостійної роботи
- •Змістовий модуль № 5 Методика навчання нумерації цілих невід’ємних чисел: мета, зміст, завдання
- •Теоретичний блок
- •Тема 1. Методика навчання молодших школярів у дочисловий період
- •Тема 2. Методика навчання нумерації чисел від 1 – 10 та числа 0
- •Тема 3. Методика навчання нумерації чисел у межах 100
- •Методика навчання нумерації чисел 11– 20
- •Методика навчання нумерації чисел від 21 до 100 Наочні посібники та дидактичний матеріал
- •Способи порівняння чисел:
- •Випадки додавання та віднімання на підставі знання нумерації чисел
- •Тема 4. Методика навчання нумерації у межах 1000 Наочні посібники: палички, пучки-десятки, пучки-сотні; намистинки, стрижні–десятки, площадки–сотні; таблиця розрядів.
- •Тема 5. Методика навчання нумерації багатоцифрових чисел
- •Читання багатоцифрових чисел
- •Запис багатоцифрових чисел
- •Читання багатоцифрових чисел
- •Питання для самоконтролю
- •Практичний блок
- •Додаткова література
- •Практичні завдання
- •Рефлексія
- •Практичне заняття № 2
- •Основна література
- •Додаткова література
- •Рефлексія
- •Завдання для самостійної роботи
- •Методичні рекомендації до виконання самостійної роботи
- •Теоретичний блок
- •Тема 1. Методика навчання табличного додавання та віднімання чисел в межах 10
- •Тема 2. Методика навчання табличного додавання та віднімання чисел з переходом через десяток
- •Тема 3. Методика навчання додавання та віднімання двоцифрових чисел
- •Усне додавання та віднімання з переходом через розряд
- •Методика навчання письмового додавання та віднімання двоцифрових чисел
- •Тема 4. Методика навчання додавання та віднімання в межах 1000.
- •Усні прийоми додавання та віднімання в межах 1000
- •Письмові прийоми додавання та віднімання в межах 1000
- •Тема 5. Методика навчання додавання та віднімання багатоцифрових чисел
- •Письмове додавання та віднімання
- •Додавання та віднімання іменованих чисел
- •Питання для самоконтролю
- •Практичний блок Практичне заняття № 1
- •Основна література
- •Додаткова література
- •Практичні завдання
- •Практичне заняття № 2
- •Основна література
- •Додаткова література
- •Практичні завдання
- •Рефлексія
- •Завдання для самостійної роботи
- •Методичні рекомендації до виконання завдань самостійної роботи
- •Теоретичний блок
- •Тема 1. Методика навчання табличного множення та ділення
- •Зміст і методика підготовчого етапу
- •Ознайомлення з арифметичною дією множення та ділення
- •Назви компонентів і результатів арифметичних дій множення та ділення
- •Переставний закон дії множення
- •Взаємозв’язок множення та ділення
- •Властивості множення та ділення з 0 та 1
- •Множення та ділення на 10
- •Ділення на рівні частини
- •Методика складання таблиць множення та ділення
- •Знаходження невідомого множника, діленого та дільника
- •Збільшення або зменшення числа в кілька разів. Кратне порівняння.
- •Зміна добутку залежно від зміни одного з множників. Зміна частки в залежності від зміни діленого. Зміна частки в залежності від зміни дільника.
- •Тема 2. Методика навчання позатабличного множення та ділення
- •Позатабличне множення та ділення
- •Множення та ділення круглого числа на одноцифрове. Ділення круглого числа на кругле.
- •Ділення з остачею
- •Розподільний закон множення відносно додавання
- •Розподільний закон ділення відносно додавання
- •Ділення двоцифрового та трицифрового числа на одноцифрове
- •Ділення на кругле число способом підбору
- •Ділення на двоцифрове число способом підбору
- •Тема 3. Методика навчання письмового множення та ділення в межах 1000
- •Письмове множення трицифрового на одноцифрове число
- •Письмове ділення трицифрового числа на одноцифрове
- •Ознайомлення з письмовим прийомом ділення
- •Письмове множення та ділення на круглі числа
- •Письмове множення на двоцифрове число
- •Письмове множення на двоцифрове число
- •Письмове ділення на двоцифрове число
- •Тема 4. Методика навчання письмового множення та ділення багатоцифрових чисел
- •Письмове множення багатоцифрового числа на одноцифрове
- •Множення одноцифрового числа на багатоцифрове
- •Ділення багатоцифрових чисел на одноцифрові
- •Множення багатоцифрових чисел, які містять нуль в середині запису .
- •В 5648 ! 856 706 4 0 48 48 0ипадки ділення на одноцифрове число, коли в середині запису частки зустрічаються нулі.
- •Множення чисел, що закінчуються нулями
- •Ділення чисел, що закінчуються нулями
- •Методика вивчення множення багатоцифрових чисел на двоцифрове число Множення та ділення на числа, які закінчуються нулями
- •Множення чисел, що закінчуються нулями
- •Письмове множення на двоцифрове число
- •Письмове ділення на двоцифрове та трицифрове число
- •Практичний блок Практичне заняття 1, 2
- •Основна література
- •Практичні завдання
- •Практичне заняття 3, 4.
- •Основна література
- •Практичні завдання
- •Рефлексія
- •Завдання для самостійної роботи
- •Методичні рекомендації до виконання завдань самостійної роботи
- •Змістовий модуль 8, 9
- •Методика навчання учнів розв'язування сюжетних задач
- •Ключові поняття:
- •Теоретичний блок
- •Тема 1. Загальні питання методики навчання розв’язування задач
- •Класифікація простих задач
- •1.Ознайомлення з задачею. Аналіз тексту задачі.
- •Тема 2. Методика формування вмінь розв’язувати сюжетні задачі
- •Методика формування загального вміння розв’язувати задачі
- •1День , 1 вів. - ? кг
- •Питання для самоперевірки
- •Практичний блок Практичне заняття № 1, 2
- •Основна література
- •Додаткова література
- •Практичні завдання
- •Практичне заняття № 3, 4
- •Основна література
- •Додаткова література
- •Практичні завдання
- •Рефлексія:
- •Завдання для самостійної роботи
- •Методичні рекомендації для виконання завдань самостійної роботи
- •Методика навчання освітньої галузі "математика" в початковій школі
- •6.010100 "Початкове навчання"
- •1. Пояснювальна записка
- •2. Зміст програмового матеріалу загальні питання методики Змістовий модуль 1, 2
- •Змістовий модуль 3,4 Сучасні навчальні технології в змісті початкової математичної освіти
- •Часткові питання методики Змістовий модуль 5
- •Змістовий модуль 6, 7
- •Змістовий модуль 8, 9
- •Змістовий модуль 10
- •Змістовий модуль 11
- •Змістовий модуль 12
- •3. Модульний план навчального курсу та методичний коментар до нього
- •Структура курсу "Методика навчання освітньої галузі "Математика" в початковій школі"
- •Модульний план навчального курсу "Методика навчання освітньої галузі "Математика" в початковій школі"
- •4. Система контролю та критерії оцінювання навчальної діяльності студентів
- •Основні вимоги до навчальних досягнень студентів
- •Оволодіння майбутніми учителями початкової школи предметною (математичною) компетентністю визначається за сукупністю інших критеріїв.
- •Рекомендована література до курсу Основна література
- •Додаткова література
- •Методика навчання математики в початковій школі: теорія і практика
Класифікація простих задач
|
№
|
Тип задачі |
Вид задачі |
Схематичний рисунок |
|
1 |
Співвідно-шення додавання Слова-ознаки співвідно-шення „всього” або його синоніми (або „було” – „стало”). Головний член співвідно-шення А той, в опис якого входить слово-ознака „всього” або „стало” (це ціле). Головний член дорівнює сумі інших членів співвідно-шення. Інші члени знаходять за правилом знаходження невідомого компонента.
|
1. Задачі на знаходження суми двох доданків 1) У Наталки 7 зошитів у лінійку та 3 зошити у клітинку. Скільки всього зошитів в Наталки? 2) У Наталки було 4 зошити, мама їй купила 5 зошитів. Скільки зошитів стало в Наталки? 2. Задачі на знаходження невідомого доданка 1) У Наталки всього 10 зошитів, з них 7 зошитів у лінійку. Скільки зошитів у клітинку в Наталки? 2) У Наталки було 4 зошити, після того як мама їй купила кілька зошитів, в неї стало 9 зошитів. Скільки зошитів купила мама? 3. Задачі на знаходження суми трьох доданків В Іринки 3 зошити, у Сашка 2 зошита, в Миколи 4 зошити. Скільки всього зошитів у дітей? 4. Задачі на знаходження третього числа за сумою двох даних чисел В Іринки 3 зошити, у Сашка 2 зошити, а в Миколи стільки зошитів, скільки в Сашка та Іринки разом. Скільки зошитів у Миколи? |
К В
?
А
?
? |
|
2 |
Співвідно-шення віднімання Слова-ознаки співвідно-шення „було” - „за-лишилося”. Головним членом А є той, в опис якого входить слово-ознака „залишило-ся”, він є різницею двох інших членів співвідно-шення К і В, де К той член, в опис якого входить слово-ознака „було”.
|
В Наталки було 7 зошитів, вона витратила 3 зошити. Скільки зошитів залишилося в Наталки?
Після того, як Наталка витратила 3 зошити, в неї залишилося 4 зошити. Скільки зошитів було в Наталки?
У Наталки було 7 зошитів, після того, як вона витратила кілька зошитів, у неї залишилося 4 зошити. Скільки зошитів витратила Наталка? |
В ?
В А
? А
|
|
3 |
Співвідно-шення різницевого порівняння Слова-ознаки співвідно-шення „ на ... менше (більше)”. Головний член співвідно-шення А той, в описі якого стоїть слово-ознака – прийменник „на”, цей член є різницею двох значень К і В однієї й тієї самої величини, що порівнюються, де К > В. |
У Наталки 6 зошитів у клітинку та 4 зошити в лінійку. На скільки більше зошитів у клітинку, ніж у лінійку в Наталки? На скільки менше зошитів у лінійку, ніж у клітинку?
У Наталки 4 зошити в лінійку, а в клітинку на 2 зошити більше. Скільки зошитів у клітинку в Наталки? У Наталки 6 зошитів у клітинку, а в лінійку на 2 зошити менше. Скільки зошитів у лінійку в Наталки? |
В
К
В
?
Стільки ж без А
? |
|
4 |
Співвідно-шення переходу від більшої одиниці лічби або вимірюван-ня до меншої. Ознакою цього виду співвідно-шення є те, що один і той самий об’єкт перерахова-ний або виміряний двома різними одиницями (мірками) – більшою і меншою і вказано, що кожна більша одиниця містить по В дрібних одиниць. Головним членом А співвідно-шення є результат лічби або вимірюван-ня об’єкта дрібними одиницями. |
Скільки олівців у 3 коробках, якщо в кожній по 6 олівців?
|
В
?
|
|
5 |
Співвідно-шення розбиття цілого на рівні частини. Ознакою цього виду співвідно-шення є те, що К розбито на А рівних частин, в кожній з яких „по” В одиниць. Головним членом співвідно-шення є А – результат розбиття К на частини по В одиниць в кожній. |
Риску довжиною 15 дм розрізали на 5 рівних частин. Яка довжина кожної частини?
Риску довжиною 15 дм розрізали по 3 дм. Скільки одержали таких частин? |
К
А разів ? або
?
А К
? разів В Або
В
? |
|
6 |
Співвідно-шення кратного порівняння Слова-ознаки співвідно-шення „ у ...більше (менше)”, Головний член А співвідно-шення той, в опис якого входить вираз „разів”, він є результатом кратного порівняння (відношен-ня) двох значень К і В однієї й тієї самої величини, при чому К > В.
|
В Іринки 8 зошитів у клітинку і 4 зошити в лінійку. У скільки разів більше зошитів у клітинку, ніж у лінійку в Іринки? У Скільки разів менше зошитів у лінійку, ніж у клітинку?
В Іринки 4 зошити в лінійку, а в клітинку в 2 рази більше. Скільки зошитів у клітинку в Іринки? В Іринки 8 зошитів у клітинку, а в лінійку в 2 рази менше. Скільки зошитів у лінійку в Іринки? |
К
В Або
В
?
В
? або
В
А |
|
7 |
Співвідно-шення частин і цілого Слова-ознаки співвідно-шення: „складає ... частину ... від”. Головний член А співвідно-шення той, у завдання якого входить слово-ознака „частина”, він є результатом ділення членів К і В на значення однієї і тієї самої величини, при цьому К<В.
|
Тато
посадив 12 дерев, а Сашко
Сашко
посадив 3 дерева, що складає
Тато посадив 12 дерев, а Сашко 3. Яку частину дерев посадив Сашко від тих дерев, що посадив тато? |
Б
А частин ? або
?
А частин В або
К
В |
|
8 |
Співвідно-шення -залежність між значеннями різних величин. Ознака співвідно-шення – явне завдання в умові задачі двох різних величин, які, як відомо, пов’язані якоюсь функціона-льною залежністю. Головним членом А цього співвідно-шення є загальна величина
|
1. Задачі на знаходження значення загальної величини (вартості, загальної довжини, загального об’єму, загальної маси, загального виробітку, відстані, площі прямокутника тощо) Скільки всього кілограмів помідорів у 3-х ящиках, якщо в кожному ящику по 8 кг помідорів?
( ціни, довжини 1-го відрізка, об’єму 1-ої посудини, маси 1-го предмету, продуктивності праці, швидкості тощо) В 3 ящиках 24 кг помідорів. Скільки кілограмів помідорів у одному такому ящику?
У ларьок привезли 24 кг помідорів у ящиках по 8 кг у кожному. Скільки ящиків з помідорами привезли в ларьок? |
К
В
?
В
К
? |
Подані види задач пропонуються протягом чотирьох перших років навчання. Природно, що найбільша кількість нових видів простих задач припадає на перші два роки навчання. У подальшому навчанні береться до уваги, що вміння розв’язувати прості задачі вже сформовано і на перший план виступає формування вміння розв’язувати складені задачі.
Під складеною задачею розуміють таку задачу, на запитання якої не можна відповісти відразу, виконавши одну арифметичну дію; для розв’язання складеної задачі треба виконати дві і більше арифметичні дії.
Для класифікації складених задач немає єдиної основи, тому їх можна поділити на дві групи. До першої групи відносяться складені задачі, які містять різноманітні поєднання відомих видів простих задач, крім співвідношення залежності між значеннями різних величин. Ці задачі можна записати коротко схематично, причому на цьому короткому записі майже завжди можна виділити складові прості задачі.
До другої групи відносяться задачі, в яких явища, що описуються, характеризуються кількома взаємопов’язаними величинами, тобто містять співвідношення залежності між значеннями різних величин. Короткий запис таких задач доцільніше подавати у формі таблиці.
Складені задачі першої групи можна класифікувати за назвою простої задачі, що має розв’язуватися останньою. Отже, існують такі види складених задач: задачі на знаходження остачі (різниці); задачі на знаходження суми; задачі на знаходження невідомого доданка; задачі на знаходження невідомого зменшуваного; задачі на знаходження невідомого від’ємника; задачі на збільшення або зменшення числа на кілька одиниць; задачі на різницеве порівняння; задачі на знаходження добутку; задачі на знаходження частки; задачі на збільшення або зменшення числа в кілька разів; задачі на кратне порівняння; задачі на знаходження дробу від числа; задачі на знаходження числа за його дробом.
Другу групу складених задач (задачі, що містять пропорційні величини) доцільно розділити на дві підгрупи:
задачі, що містять знаходження суми, різницеве чи кратне порівняння: на знаходження суми двох добутків (часток); задачі, обернені до задач на знаходження суми двох добутків (часток); на різницеве порівняння двох добутків (часток); задачі, обернені до задач на різницеве порівняння двох добутків (часток); задачі на кратне порівняння двох добутків (часток); задачі, обернені до задач на кратне порівняння двох добутків (часток); задачі, які містять різницеве (кратне) відношення;
„типові” задачі:
задачі, що містять однакову (сталу) величину (задачі на знаходження четвертого пропорційного, задачі на пропорційне ділення, задачі на знаходження невідомих за двома різницями, задачі на подвійне зведення до одиниці);
задачі на процеси ( задачі на спільну роботу, задачі на рух).
Розв’язування задачі є складним процесом розумової діяльності людини, який спрямований на перетворення об’єкта, що описаний у змісті задачі, на вирішення суперечності між умовою та вимогою задачі. Здебільшого методисти визначають чотири етапи процесу розв’язування як простої, так і складеної сюжетної задачі:
ознайомлення з задачею, аналіз тексту задачі;
пошук розв’язування задачі;
реалізація плану розв’язування задачі; запис розв’язання і відповіді;
робота над задачею після її розв’язання.
Діяльність з розв’язування задач може здійснюватися як алгоритмічним, так і евристичним способом. Якщо учень виконує приписи, то в цьому випадку здійснюється алгоритмічний спосіб діяльності з розв’язування задач, який характеризується тим, що учень здійснює власну діяльність у відповідності з відомим йому алгоритмом. Якщо, розпочинаючи розв’язання математичної задачі, учень не має орієнтувальної основи для своїх дій, то він її відшукує, виконуючи евристичну діяльність. Така діяльність здійснюється за допомогою особливих прийомів – евристик.
Вченими доведено, що домінуючою евристикою при розв’язуванні задач є моделювання як задачної ситуації (побудову допоміжних моделей – предметних, схематичних, словесних), так і процесу її розв’язування (схеми аналітичного і синтетичного розбору задачі, „дерева міркувань”), тому що саме воно забезпечує необхідне орієнтування в задачній ситуації.
Незалежно від способу (алгоритмічного чи евристичного) діяльність учнів із розв’язування задач являє собою реалізацію основних етапів щодо виконання певних дій. Перш ніж розглядати дії, за допомогою яких реалізуються етапи розв’язування задачі, необхідно акцентувати увагу на правильному розумінні таких висловлювань:
розв'язати задачу — означає встановити (розкрити, відшукати, побачити, пояснити) зв'язки між даними і шуканим числами, на основі чого дібрати потрібні арифметичні дії та їх порядок виконання, знайти результати дій, а потім відповісти на запитання задачі. Відповідь задачі не відгадується, а знаходиться при виконанні потрібних дій (операцій). Для знаходження шуканого числа треба вміти пояснити (розказати), які дії і над якими числами варто виконати, в якому порядку і чому саме такі відповіді на запитання задачі;
розв'язування задачі – це процес, робота, яка включає ознайомлення з текстом задачі, роздуми (міркування) над її розв'язанням, запис чи формулювання дій та відповідей.
розв'язання задачі – це запис (формулювання) порядку арифметичних дій, за допомогою яких знаходиться відповідь до задачі.
розв'язок – відповідь на запитання задачі (а ще розв'язком називають числове значення шуканої величини).





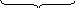

 К
?
К
?

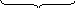

 К В
С
К В
С





 К
В
К
В

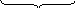



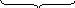
 К
К



 ?
?



 К
К







 ?
?





 Стільки
ж та А
Стільки
ж та А

 Б
Б










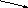


 ...
...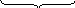 К
разів
К
разів




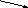

 ...
...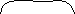
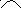 К
К









 ...
...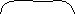
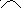 К
К










 ...
...
 скільки
разів?
скільки
разів?
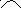 К
К






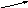

 у А разів
більше
у А разів
більше


 ...
...
 ?
?









 ...
... 1 - Б
1 - Б









 ...
... 1 - ?
1 - ?






 ?
?





 ...
... А
А





 ...
... А
А





 ...
...