Получим:
x |
E0 |
= x |
E3 |
cosϕ |
30 |
− y |
E3 |
sinϕ |
30 |
|
|
|
|
|
|||||
|
|
= x |
|
sinϕ |
|
− y |
|
cosϕ |
|
y |
E0 |
E3 |
30 |
E3 |
30 |
||||
|
|
|
|
|
+ 2 cosϕ20 |
+ 1 cosϕ10 |
; |
(2.8) |
|
+ 2 sinϕ20 |
+ 1 sinϕ10. |
|||
|
||||
Уравнения (2.8) можно было бы получить, решая уравнения (2.1), (2.2) и (2.3), но вычисления заняли бы больше времени. Матричная форма записи и решения уравнений удобнее. Для решения таких уравнений существуют стандартные программы, используемые на ЭВМ.
Уравнение (2.8), определяющее положение точки E3 относительно х0у0, можно получить и иным способом, а именно – составить уравнение проекции контура 010203E3 в системе х0у0.
Однако метод проекций получается сложнее метода преобразования координат для пространственных механизмов.
2.1.3. Определение положений, скоростей и ускорений звеньев пространственных механизмов
При кинематическом анализе механизмов по заданному закону движения ведущих звеньев определяем положение, скорость и ускорение ведомых звеньев механизма. Ведомые звенья являются исполнительными в машине, поэтому знание выше названных параметров совершенно необходимо при эксплуатации машин и механизмов.
Токарный станок. Для чего здесь необходимо знать скорости ведомых звеньев? Скорость является одним из главных факторов выбора оптимального режима резания. От скорости резания зависит чистота обработки поверхностей. Скорость надо знать.
Знание ускорений необходимо для определения сил инерции, возникающих в механизмах. С учетом сил инерции ведется силовой и прочностной расчет механизма.
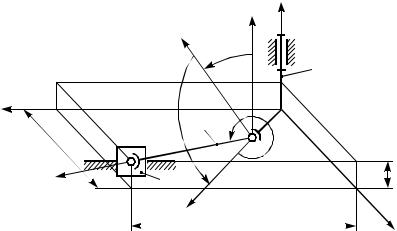
Задачу определения положений, скоростей и ускорений ведомого звена рассмотрим на примере пространственного кривошипно-ползунного механизма (рис. 2.2).
32
|
|
|
|
|
z1 |
z0 |
|
|
|
z2 |
|
||
|
|
|
θ21 |
O |
||
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
ϕ10 |
|
|
A |
x0 |
l3 |
C |
2 |
|
l1 |
|
|
l2 |
B |
ϕ21 |
|||
|
x2 |
|
|
|
|
0 |
|
|
|
3 |
|
|
l |
|
|
|
x1 |
|
|
|
|
|
|
|
x0C |
y0 |
|
|
|
|
|
Рис. 2.2 |
|
|
|
Степень свободы данного механизма равна единице, |
|||||
W=1, т.е. задана одна обобщенная координата, это угол пово- |
||||||
рота кривошипа АВ, ϕ10. Угол ϕ10 задается как функция времени.
Удобно перемещение звеньев механизма рассматривать относительно неподвижной системы координат. Неподвижную систему координат связываем со стойкой механизма. Ось x0 неподвижной системы направим параллельно линии движения ползуна, ось у0 будет направлена перпендикулярно линии движения ползуна. Причем плоскость х0Ау0 выбирается еще и так, чтобы кривошип АВ лежал в этой плоскости. Ось z0 направим по оси вращения кривошипа.
Обозначим координату точки С по оси у0 через l3, а по оси z0 через l0. Текущее значение перемещения точки С будет определяться одной переменной координатой x0C по оси х0.
Выберем еще две подвижные системы координат. Одну свяжем с кривошипом, вторую с шатуном. С шатуном свяжем систему x2y2z2, где x2 направим по шатуну ВС, z2 – по оси пальца шатуна, y2 перпендикулярно плоскости x2Вz2. Такой в ыбор системы координат позволяет определить положение точки С в системе x2y2z2 одной координатой, а именно:
33
x2 |
= 2; |
|
= 0; . |
y2 |
|
|
= 0. |
z2 |
Чтобы выразить перемещение ползуна х0С
(2.9)
через обоб-
щенную координату ϕ10, подвижную систему x1y1z1 свяжем с кривошипом АВ так: ось z будет параллельна оси z0, ось y1
окажется в ϕ1 плоскости x0Аy0, а x1 направим по кривошипу АВ. Углы между осями x2 и x1 обозначим через ϕ21, а между z2 и z1 – через θ21. Последовательным переходом из системы
x2y2z2 в систему x1y1z1 и в систему x0y0z0 решаем задачу нахождения положения ползуна в неподвижной системе координат.
Опишем положение ползуна в системе x1y1z1.
x |
= x |
2 |
cosϕ |
21 |
; |
|
|
|
|
1C |
|
|
|
|
|
|
|
||
y1C = x2 sinϕ21 cosθ21;. |
(2.10) |
||||||||
z |
= x |
2 |
sinϕ |
21 |
cosθ |
21 |
. |
|
|
1C |
|
|
|
|
|
||||
Найденные координаты точки С в системе x1y1z1 спроектируем на оси неподвижной системы x0y0z0.
x |
0C |
= x |
|
|
cosϕ |
10 |
− y |
|
|
sinϕ |
10 |
+ |
1 |
cosϕ |
10 |
|
= |
|
|
|
|
|
|||||||
|
1C |
|
|
|
1C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
= 2 cosϕ10 |
cosϕ21 − 2 sinϕ10 sinϕ21 cosθ21 + |
|
|
|
|||||||||||||||||||||||
|
|
+ 1 cosϕ10 |
|
+ 1 cosϕ10; |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.11) |
|||||||||||
y |
= x |
|
|
sinϕ |
10 |
|
− y |
|
cosϕ |
10 |
+ |
1 |
sinϕ |
10 |
= |
|
|
|
|
||||||||||
|
1C |
1C |
|
|
|
1C |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
= |
2 |
cosϕ |
21 |
sinϕ |
10 |
+ |
2 |
sinϕ |
21 |
cosϕ |
10 |
cosθ |
21 |
+ |
1 |
sinϕ |
; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|||||||||||||
|
|
= z1C = 2 sinϕ21 sinθ21. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
z0C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Выше отмечено, что
y0C = 3 = const, z0C = 0 = const,
подставив эти значения в систему (2.11), получим:
34
x |
0C |
= |
2 |
cosϕ |
cosϕ |
21 |
− |
2 |
sinϕ |
sinϕ |
21 |
cosθ |
21 |
+ |
1 |
cosϕ |
; |
|
|
|
10 |
|
|
10 |
|
|
|
10 |
|
||||||||
|
3 |
== 2 cosϕ10 sinϕ21 |
+ 2 |
sinϕ10 |
cosϕ21 cosθ21 + 1 sinϕ10 |
; (2.12) |
||||||||||||
|
|
= 2 sinϕ21 cosθ21. |
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Система (2.12) содержит три уравнения и три неизвестных:
x0C, ϕ21, θ21.
Из второго и третьего уравнений системы (2.12) опреде-
ляем углы ϕ21 и θ21, подставляя их в первое уравнение, находим x0С, т.е. координату положения ползуна.
Если механизм будет плоским, θ20=0, т.к. оси z1z2z3 параллельны. В этом случае ползун будет двигаться в плоскости кривошипа. Система уравнений для определения положения ползуна примет вид:
x |
0C |
= |
|
cosϕ |
|
cosϕ |
|
− |
|
sinϕ |
|
sinϕ |
|
+ |
|
cosϕ |
; |
(2.13) |
|
|
2 |
|
10 |
|
21 |
|
2 |
|
10 |
|
21 |
|
1 |
10 |
|
||
3 = 2 cosϕ10 sinϕ21 |
+ 2 |
sinϕ10 cosϕ21 + 1 sinϕ10. |
|
|
||||||||||||||
Два уравнения с двумя неизвестными. Из второго уравне-
ния определяем ϕ21, подставив его в первое уравнение, определим положение ползуна в зависимости от обобщенной координа-
ты ϕ10 и размеров звеньев механизма l1, l2, l3.
Для определения скорости и ускорения перемещения ползуна необходимо систему уравнений (2.12) продифференцировать по времени.
Первое дифференцирование системы (2.12) дает возможность получить систему линейных уравнений для определения скорости перемещения ползуна.
Из третьего и второго уравнения полученной системы
(2.14) находим ϕ21 и θ21, подставив их в первое уравнение, получим возможность определить скорость перемещения ползуна
xOC в зависимости от угла поворота ϕ10 кривошипа и угловой
скорости ϕ10 кривошипа. Повторное дифференцирование уравнений системы (2.12) позволяет определить ускорение xOC
ползуна.
35