W=6n–5Р5–4Р4–3Р3

Условие существования группы: Wгр. = 0

6n=5Р5+4Р4+3Р3

В этом случае n=2; Р5=1; Р4=1; Р3=1

Если такую группу присоединим к начальному звену, движение которого определяет одна обобщенная координата, получим пространственный механизм со степенью свободы, равной единице (рис. 1.27)

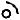2 3

1

n=3;Р5=2; Р4=1; Р3=1; W=6×3–5×2–4×1–3×1=1.

Рис. 1.27

Следовательно, принцип образования пространственных механизмов сохраняется.

2.АНАЛИЗ МЕХАНИЗМОВ

2.1.Кинематический анализ механизмов

Кинематический анализ механизмов – это изучение движения звеньев механизма без учета сил, вызывающих движение. Определяющим фактором здесь является степень свободы механизма. Закон движения ведущих (начальных) звеньев известен, поэтому можно сказать, что кинематический анализ состоит в определении движения звеньев механизма по заданному движению начальных звеньев.

26

Основные задачи кинематического анализа следующие:

1)определение положений звеньев, включая определение траектории движения отдельных точек;

2)определение передаточных функций, скоростей и ус-

корений звеньев механизма.

Методы кинематического анализа:

1)аналитические;

2)графоаналитические;

3)графические;

4)экспериментальные.

В настоящее время аналитические методы анализа выходят на первое место, чему способствует развитие ЭВМ. Однако графоаналитические и графические методы хотя и уступают в точности получаемых результатов, широко распространены изза своей наглядности и доступности.

Ниже рассмотрено аналитическое решение задачи о положениях звеньев механизма по методу преобразования координат. Метод предложен Ю.Ф. Морошкиным.

2.1.1. Определение положений звеньев плоской незамкнутой кинематической цепи

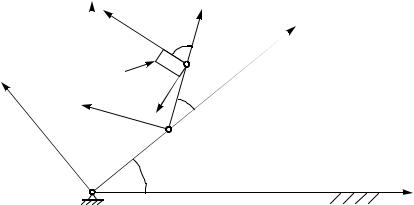
Также кинематические цепи лежат в основе манипуляторов. Рассмотрим четырехзвенную незамкнутую цепь только с вращательными парами 5-го класса, оси кинематических пар параллельны, т.е. цепь плоская (рис. 2.1). Определим степень свободы кинематической цепи.

Необходимо задать три обобщенные координаты, чтобы положение звеньев относительно стойки было определено. В

качестве обобщенных координат примем углы ϕ10, ϕ21, ϕ32. Углы должны быть заданы как функция времени. Заданы размеры звеньев l1 и l2 и положение точки Е3 на звене 3. Положение точки Е3 задано координатами хЕ3 и yЕ3. Требуется найти траекторию точки Е3 относительно стойки.

27

n=3; Р5=3; W=6×3–2×3=3.

Рис. 2.1

Со стойкой свяжем неподвижную систему координат х0, у0. Выберем системы координат х1у1, х2у2 и х3у3, связав их с положением звеньев кинематической цепи.

Положение точки Е3 звена 3 задано в системе координат х3у3 ; необходимо найти ее положение в системе х0у0 , т.е. найти координаты хЕ0 и yЕ0. Переход от системы х3у3 к системе х0у0 проведем постепенно, переходя из третьей системы во вторую, из второй в первую, из первой в нулевую.

Найдем положение точки Е3 в системе х2у2.

Переходим в систему х1у1, находим координаты хЕ1 и yЕ1.

Переходим в систему х0у0, находим координаты

Е3=хЕ0,yЕ0.

28

Уравнения (2.1), (2.2) и (2.3) являются системой линейных уравнений с шестью неизвестными. Они дают возможность определить траекторию точки Е3 , т.е. определить е положение относительно системы х0у0. Метод преобразования координат более удобен, если воспользоваться матричной формой.

2.1.2. Матричная форма уравнения преобразования координат точек звеньев

Матрица порядка (m×n) есть система чисел (элементов), расположенных в виде прямоугольной таблицы из m строк и n столбцов:

a11,a12 ,........,a1n A= a21,a22 ,........,a2n .

........................

an1,an2 ,........,ann

Если m=n, то матрица называется квадратной порядка n. Уравнения (2.1), (2.2) и (2.3) запишем в матричной фор-

ме. Коэффициенты правой части дают матрицу порядка (2×3). Удобнее использовать матрицы квадратные, поэтому к каждым

двум уравнениям добавим тождество l≡1, получим квадратные матрицы третьего порядка.

Составим матрицу перехода из системы х3у3 в систему

х2у2.

Запишем матрицу перехода Т21. 29

Левые части уравнений (2.1), (2.2) и (2.3) с добавлением тождества l≡1 дают столбцевые матрицы третьего порядка:

Подставим уравнения (2.4) и (2.5) в уравнение (2.6), подучим

rE0 =T10 ×T21 ×T32 ×rE3 .

Это уравнение позволяет определить положение точке Е3 в системе координат х0у0. Для этого необходимо перемножить

матрицы T10 и Т21, а затем (T10Т21)T32 и столбцевую rE3 .

a11 = cosϕ10 cosϕ21 − sinϕ10 sinϕ21 = cos(ϕ10 +ϕ21 )= cosϕ20; a12 = −cosϕ10 sinϕ21 − sinϕ10 cosϕ21 = −sin(ϕ10 +ϕ21 )= −sinϕ20;

a13 = 1 cosϕ10;

a21 = sinϕ10 cosϕ21 +cosϕ10 sinϕ21 = sinϕ20; a22 = −sinϕ10 sinϕ21 +cosϕ10 cosϕ21 = cosϕ20; a23 = 1 sinϕ10.

матрицу rE3 :

xE3 rE3 = yE3 .

1

31