
- •1. СТРУКТУРА МЕХАНИЗМОВ
- •1.2. Классификация кинематических пар
- •1.3. Структура и кинематика плоских механизмов
- •1.4. Структурная формула кинематической цепи общего вида
- •1.5. Структурная формула плоских механизмов
- •1.6. Пассивные связи и лишние степени свободы
- •1.7. Замена в плоских механизмах высших кинематических пар низшими
- •1.8. Классификация плоских механизмов
- •1.9. Структурные группы пространственных механизмов
- •2. Анализ механизмов
- •2.1. Кинематический анализ механизмов
- •2.1.1. Определение положений звеньев плоской незамкнутой кинематической цепи
- •2.1.2. Матричная форма уравнения преобразования координат точек звеньев
- •2.1.3. Определение положений, скоростей и ускорений звеньев пространственных механизмов
- •2.1.4. Графическое определение положений звеньев механизма и построение траектории
- •2.1.5. Определение скоростей и ускорений точек звеньев методом планов
- •2.1.6. Свойство планов скоростей
- •2.1.7. Построение плана скоростей и ускорений кулисного механизма (рис. 2.7)
- •2.1.8. Аналоги скоростей и ускорений
- •2.2. Силовой анализ механизмов
- •2.2.1. Условие статической определимости кинематических цепей
- •2.2.2. Силы, действующие на звенья механизма
- •2.2.3. Силы инерции звена, совершающего возвратно-поступательное движение
- •2.2.4. Силы инерции звена, совершающего вращательное движение вокруг неподвижной оси
- •2.2.5. Силы инерции звена, совершающего плоское движение (рис. 2.17)
- •2.3.1. Силовой расчет начального звена (рис. 2.18, а)
- •3. МЕХАНИЗМЫ С ВЫСШИМИ ПАРАМИ. ЗУБЧАТЫЕ МЕХАНИЗМЫ
- •3.1. Зубчатые передачи
- •3.1.1. Общие сведения. Основная теорема зацепления
- •3.1.2. Геометрические элементы зубчатых колес
- •4. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
- •4.1. Строительные конструкции
- •4.2.1. Конечные элементы, используемые для моделирования конструкции разъемного соединения трубопровода
- •4.2.1.1. Объемный элемент в форме прямой треугольной призмы (пентаэдр)
- •4.2.2. Пластинчатый элемент треугольной формы
- •4.2.3. Пластинчатый элемент четырехугольной формы
- •4.2.4. Моделирование статического состояния разъемного соединения
- •5.1. Стадии проектирования
- •5.2. Основные термины и определения
- •6. ОСИ И ВАЛЫ
- •6.1. Общие сведения
- •6.2. Проектный расчет валов и осей
- •6.2.1. Составление расчетных схем
- •6.3. Проверочные расчеты валов и осей
- •6.3.1. Расчет на выносливость валов и вращающихся осей
- •6.3.2. Расчет валов и неподвижных осей на статическую прочность
- •6.4. Проверочный расчет валов и осей на жесткость
- •7. ПОДШИПНИКИ, МУФТЫ
- •7.1. Подшипники
- •7.1.1. Подшипники скольжения
- •7.1.2. Подшипники качения
- •7.2. Муфты
- •7.2.1. Волновые передачи
- •8. Расчет простейших осесимметрично нагруженных тонкостенных оболочек вращения
- •8.1. Сферические оболочки
- •8.2. Цилиндрические оболочки (рис. 8.3)
- •9. Ременные передачи
- •9.1. Общие сведения
- •9.1.1. Классификация
- •9.1.2. Типы приводных ремней
- •9.2. Кинематические и силовые зависимости
- •9.2.1. Напряжения в ремне
- •9.2.2. Относительное скольжение ремня
- •9.2.3. Расчет передач по кривым скольжения
- •9.2.4. Допустимое полезное напряжение
- •9.2.5. Клиноременная передача
- •9.2.6. Расчет клиноременных передач
- •10. 3аклепочные соединения
- •11. Сварные соединения
- •12. Шпоночные соединения
- •13. Резьбовые соединения
- •13.1. Расчет на прочность стержня болта (винта) при различных случаях нагружения
- •13.2. Расчет соединений, включающих группу болтов
- •14. ПОРШНЕВЫЕ КОМПРЕССОРЫ И ДЕТАНДЕРЫ. МЕМБРАННЫЕ КОМПРЕССОРЫ
- •14.1. Конструкции поршневых компрессоров
- •14.2. Конструктивные схемы поршневых детандеров
- •14.3. Мембранные компрессоры
- •заключение
- •Библиографический список

Полученный механизм (обращенный механизм) представляет ступенчатую передачу, передаточное отношение которой
U(H ) = |
ω1 −ωH . |
|||
14 |
ω |
4 |
−ω |
H |
|
|
|
||
Из последней формулы можно определить передаточное отношение для планетарного механизма (ω4 =0):
U14(H ) = ω−1 −ωωH =1−U1(H4) .
H
Передаточное отношение планетарного механизма при ведущем водиле
UH(41) = U1(4) ,
1H
где U1(H4) передаточное отношение при ведущем центральном колесе 1.
4. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
МКЭ первоначально появился в строительной механике, сейчас он широко применяется во многих научных и инженерных приложениях.
МКЭ характеризуется следующими свойствами:
1)физическая область делится на подобласти или конечные элементы;
2)зависимая переменная (одна или несколько) аппраксимируется функцией специального вида на каждом конечном
элементе и, следовательно, во всей области. Параметры этих аппроксимаций в последующем становятся неизвестными параметрами задачи;
3) подстановка аппроксимаций в определяющие уравнения дает систему множества уравнений с неизвестными параметрами. Решая эти уравнения, можно определить значения этих параметров и, следовательно, получить приближенное
71
решение задачи. Так как число неизвестных в окончательной системе уравнений часто весьма велико, то общепринято использовать матричные обозначения как для сокращения записи, так и для облегчения программирования.
Метод конечных элементов предполагает процедуру решения для непрерывной системы, т.е. системы, охватывающей явление в непрерывной области.
4.1. Строительные конструкции
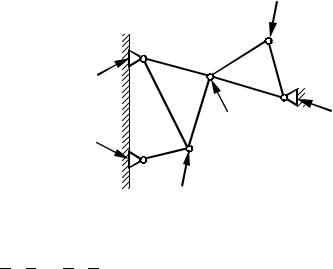
Рассмотрим плоскую шарнирно-соединенную ферму. Предполагается, что ферма собрана без предварительного напряжения, а нагрузки приложены в узлах (рис. 4.1).
|
|
|
|
R3 |
|
_ |
6 e |
|
e6 |
3 |
|
R6 |
1 |
2 |
|
e |
|
|
|
|
7 |
_ |
|
|
|
|
|
|
|
|
e2 |
e4 |
_ e5 1 |
R1 |
|
_ |
e3 |
R2 |
|
|
|
4 |
|
|
|
||
R5 |
5 |
_ |
|
|
|
|
|
R4 |
|
|
|
|
|
Рис. 4.1 |
|
|
|
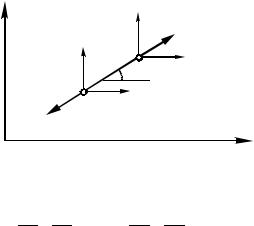
Силы F2 |
и F3, действующие в шарнирах на типовой |
||||
элемент е6, представлены |
на |
рис. 4.2 в виде их прое кций |
|||
Fx2 ,Fy2 и Fx3 ,Fy3 на оси х, у соответственно.
Смещения узлов элемента от их исходного положения (до приложения нагрузки) обозначим δ2 и δ3 с компонентами
δx2, δy2 и δx3, δy3 соответственно. В матричной форме:
72
[F]e6
[δ ]e6
|
|
|
|
|
|
F |
e6 |
|
|
|||
F2 e6 |
|
x2 |
|
|
|
|||||||
= |
Fy2 |
|
, |
(4.1) |
||||||||
= F |
|
|
F |
|
||||||||
3 |
|
|
x3 |
|
|
|
||||||
|
|
|
|
|
|
F |
|
|
|
|||
|
|
|
|
|
|
|
y3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
e6 |
|
δx2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
δ |
2 |
|
|
|
|
|||||||
|
|
δy2 |
|
|
, |
(4.2) |
||||||
= |
|
|
|
|
= |
|
|
|
|
|
||
|
|
|
|
|
|
|||||||
δ |
|
|
|
|
δ |
|
|
|
|
|
||
|
3 |
|
|
|
x3 |
|
|
|
||||
|
|
|
|
|
|
|
δ |
y3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где индекс е6 обозначает элемент, к которому относятся рассматриваемые величины.
y |
|
Fy |
_ |
|
_ |
|
|||
|
3 |
P |
||
|
|
|||
Fy |
|
|
||
|
3 |
_ |
||
2 |
e6 |
|||
|
|
|||
2 |
Θ |
Fx |
||
|
_ |
3 |
||
|
|
|||
_ |
|
|
||
|
Fx |
|
||
P |
|
|
||
|
2 |
|
||
|
|
|
||
0 |
Рис. 4.2 |
x |
||
|
|
|||
Растяжение или сжатие стержня длины L определяется величиной
(δx3 −δx2 )cosθ + (δy3 −δy2 )sinθ ,
деформация получается в результате деления этой величины на L. Так как напряжение (σ) равно модулю Юнга Е, умноженному на деформацию, то продольная сила, приложенная к
стержню, определяется как
Р = (EA)[( |
|
− |
|
)cosθ +( |
|
|
− |
|
|
)sinθ], |
(4.3) |
δx |
δx |
δy |
|
δy |
|
||||||
L |
3 |
2 |
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
где А – площадь поперечного сечения стержня. 73

Компоненты продольной силы Р могут быть приравнены к компонентам шарнирных сил, и уравнение (4.1) примет вид
|
|
|
|
|
|
|
|
Fx2 |
|
− Pcosθ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
F2 |
|
|
|
|
− Psinθ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
e |
|
|
Fy2 |
|
|
|
|
|
|
|
|
|
|
|
|
(4.4) |
||||||||||||||
|
|
[F]6 = |
|
|
|
= |
|
= |
Pcosθ |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
F3 |
|
|
Fx3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
F |
|
|
Psinθ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
y3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подстановка Р из уравнения (4.3) в выражение для Fx2 в |
|||||||||||||||||||||||||||||||
уравнении (4.4) дает |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Fx2 = (EA)[−( |
|
− |
|
)cos2 θ −( |
|
− |
|
)sinθ cosθ], |
(4.5, а) |
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
δx2 |
δy3 |
δy2 |
|||||||||||||||||||||||||||||
|
δx3 |
|||||||||||||||||||||||||||||||
или |
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fx2 = (EA)×[cos2 θδx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
+ sinθ cosθδy2 |
|
|
|
|
|
|
|
(4.5, б) |
||||||||||||||||||||||
|
|
|
L |
|
|
|
|
− sinθ cos |
|
|
|
]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
−cos2 θδx |
|
θδy |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
В матричной форме уравнение (4.5, б) имеет вид: |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
= (EA)[cos2 θ,sinθ cosθ,−cos2 θ ,−sinθ cosθ]× |
|
δx2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Fx2 |
δy2 |
|
. |
(4.5, в) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
δ |
|
|
|
|||||||||||||||||||||||||||||
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y3 |
|
|
||||
|
Четыре уравнения типа (4.5, в) для |
|
Fx |
2 |
,Fy |
2 |
,Fx ,Fy |
3 |
в мат- |
|||||||||||||||||||||||
ричной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Fe6 |
= |
(EA)× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 θ ,sinθ cosθ ,−cos2 |
θ ,− sinθ cosθ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
δx2 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(4.6, а) |
|||||
|
|
|
|
, |
− sinθ cosθ ,− sin2 θ |
|
δy2 |
|
||||||||||||||||||||||||
|
|
sinθ cosθ ,sin2 θ |
|
|
|
|||||||||||||||||||||||||||
|
× |
−cos2 θ ,− sinθ cosθ ,cos2 θ ,sinθ cosθ |
|
× |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
δ |
x3 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2 |
θ ,sinθ cosθ ,sin |
2 |
θ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
δ |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
− sinθ cosθ ,− sin |
|
|
|
|
y3 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С множителем EAL , внесенным в квадратную матрицу, уравнение (4.6, а) приобретает вид
|
|
|
Kx2 ,x2 Kx2 ,y2 |Kx2 ,x3 Kx2 ,y3 |
|
|
|
|
|
|
|
|
||||||||||||
|
F |
|
δx |
|
|
||||||||||||||||||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
Ky2 ,x2 |
Ky2 ,y2 |
|Ky2 ,x3 Ky2 ,y3 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||||||
e6 |
Fy2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δy2 |
|
|
|
||||
F |
|
|
= −−−−−− |−−−−−−− |
|
|
|
|
|
|||||||||||||||
= Fx |
|
|
|
|
|
. |
(4.6, б) |
||||||||||||||||
δ |
|
|
|
||||||||||||||||||||
|
|
3 |
|
Kx3 ,x2 Kx3 ,y2 |Kx3 ,x3 Kx3,y3 |
|
|
|
x3 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ |
|
|
|
|
|
||
|
Fy3 |
|
|
,x |
Ky |
,y |
|
|Ky ,x |
Ky |
,y |
|
|
|
|
|
||||||||
|
|
|
|
Ky |
2 |
3 |
|
y3 |
|
|
|
||||||||||||
|
|
|
|
|
3 |
2 |
3 |
|
3 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
||
Если матрицы разбиты штриховыми линиями, то уравнение (4.6, б) можно записать следующим образом:
|
|
K22e6 |
K23e6 |
|
|
|
|
|
F |
e |
δ |
2 |
(4.6, в) |
||||
6 |
= |
|
|
|
. |
|||
|
|
Ke6 |
Ke6 |
|
δ |
3 |
|
|
|
|
32 |
33 |
|
|
|
||
Уравнение (4.6, в) является матричным уравнением для элемента е6, и его квадратная матрица коэффициентов [К] называется матрицей жесткости элемента. Подобные уравнения могут быть получены и для других элементов. Уравнен ие (4.6, в) может быть расширено так, чтобы оно включало все узловые смещения системы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
0 |
|
|
|
0 0 0 |
0 0 0 |
δ1 |
|
||||||||||||||
|
|
Fe6 |
|
0 |
|
|
|
|
0 0 0 |
|
|
|
|
|
|
|
|
||||||
|
|
Ke6 |
Ke6 |
δ2 |
|
|
|
||||||||||||||||
|
|
|
2 |
|
|
|
|
22 |
|
23 |
|
|
|
|
|
|
|
|
|
|
|||
|
e |
|
|
e6 |
|
|
0 |
K |
e6 |
K |
e6 |
0 0 0 |
|
δ |
3 |
|
|
|
|||||
|
F |
|
|
|
32 |
33 |
|
|
|
|
|
|
|||||||||||
[F |
6 |
]= |
3 |
|
= |
|
|
|
|
|
|
|
|
|
|
. |
(4.6, г) |
||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||
|
|
0 |
|
|
|
0 0 |
0 0 0 |
δ4 |
|
|
|
||||||||||||
|
|
0 |
|
|
|
0 0 |
0 |
0 0 0 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
δ |
5 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ |
|
|
|
|
|
||||||||||
|
|
0 |
|
|
|
0 0 |
0 0 0 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
75 |
|
|
|
|
|
|
|
|
|
|
|
|
|

Уравнение (4.6, г) представляет собой расширенное матричное уравнение для элемента е6:
[F]e6 =[ |
|
e6 ]{δ}, |
(4.6, д) |
K |
где [Ke6 ] – расширенная матрица жесткости элемента е6,
{δ} – вектор узловых перемещений системы.
Внешние силы R1, R2, …R6 могут быть выражены через
х–у компоненты Rx1 ,Ry1 ,Rx2 ,Ry2 ... Rx6 ,Ry6 ,а условия равновесия в узловых точках могут быть определены через эти компонен-
ты. Например, в узле с номером 2 условие равновесия в направлении х имеет вид
R |
= Fe1 |
+ Fe4 |
+ Fe5 |
+ Fe6 . |
(4.7) |
x2 |
x2 |
x2 |
x2 |
x2 |
|
Хотя в правую часть равенства (4.7) дают вклад только те элементы, которые содержат узел 2, удобно записать это соотношение в общем виде:
7
Rx2 = ∑Fxe2i , (4.8, а)
i=1
или
7
Rx2 = ∑Fxe2 . (4.8, б)
e=1
Аналогичное соотношение получается для другой компоненты вектора R2:
7
Ry2 = ∑Fye2 . (4.8, в)
e=1
Уравнения (4.8, б) и (4.8, в) можно объединить в матри ч- ной записи:
|
R |
|
|
7 |
Fe |
|
7 |
|
R2 |
= |
x2 |
|
= ∑ xe2 |
|
= ∑F2e. |
(4.9) |
|
|
Ry |
|
e=1 |
F |
|
e=1 |
|
|
|
|
2 |
|
|
y2 |
|
|
|
|
|
|
|
|
76 |
|
|
|

Аналогичные уравнения могут быть записаны и для других узлов. Результирующая система уравнений равновесия записывается в виде
|
R1 |
|
|
F1e |
|
|
|
|
|
||
|
R |
|
7 |
Fe |
|
7 |
e |
|
|
||
R = |
2 |
|
= ∑ |
2 |
|
= ∑F |
. |
(4.10) |
|||
|
|
|
|
|
|||||||
|
|
|
e=1 |
|
|
e=1 |
|
|
|
||
|
|
|
|
|
|
||||||
|
R6 |
|
|
Fe |
|
|
|
|
|
||
|
|
|
|
6 |
|
|
|
|
|
||
Подставим выражений типа (4.6, д) в уравнение (4.10) |
|||||||||||
|
|
|
7 |
|
|
eδ |
|
|
|
|
|
|
|
R = ∑ |
|
|
|
|
(4.11) |
||||
|
|
K |
|
|
|
||||||
или |
|
|
e=1 |
|
|
|
|
|
|||
|
|
Kδ = R . |
|
|
|
|
(4.12) |
||||
|
|
|
|
|
|
|
|||||
Это уравнение называется матричным уравнением системы, а матрица К, задаваемая равенством
7 |
|
K = ∑Ke , |
(4.13) |
e=1
называется матрицей жесткости системы.
Процедура, использованная выше для объединения матричных уравнений элементов, называется поэлементным объединением. Метод анализа конструкций, описанный выше, называется методом перемещений и может быть распространен на случаи:
а) начальных конструкционных (сборочных) или тепловых деформаций;
б) массовых сил, таких как гравитационные; в) распределенных нагрузок, приложенных к стержням.
Вводя три дополнительных вектор-столбца в уравнение
(4.12), получим
Kδ + Fε0 + Fв + Fd = R, |
(4.14) |
где Fε0 , Fв , Fd соответствуют конструкционным и тепловым
деформациям в системе, массовым силам и распределенным нагрузкам.
77
Этот анализ может быть распространен на трехмерные фермы и случаи жестких соединений, когда силы и моменты передаются через узлы.
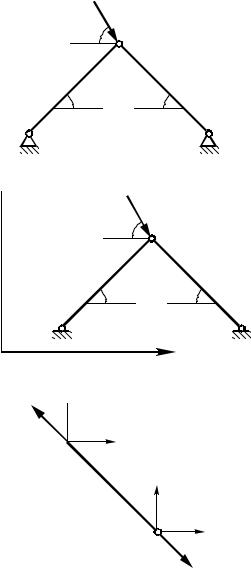
Пример
Для шарнирно-соединенной фермы (рис. 4.3) вычислить смещения в узле 2, предполагая, что каждый стержень имеет длину равную 10 см и поперечное сечение равное 1 см2. Модуль Юнга Е = 2×106 кг/см2.
Согласно уравнению (4.3), для элемента 1 сила, действующая вдоль стержня, равна
P = EAL 1 |
[( |
|
|
x2 − |
|
|
x1 )cos135 |
+ ( |
|
|
y2 |
− |
|
|
y1 )sin135 ], |
|
(4.15) |
||||||||||||||||||||
δ |
δ |
δ |
δ |
|
|||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
отсюда с помощью уравнений (4.4) и (4.6, а) получаем |
|
||||||||||||||||||||||||||||||||||||
|
Fx1 |
|
− Pcos135 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
||||||||||||||||
|
|
|
|
1 |
|
|
−1 |
|
−1 1 |
δ |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 −1 |
1 |
|
1 |
−1 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
e |
Fy1 |
|
− Psin135 |
|
|
|
δ y1 |
|
|
||||||||||||||||||||||||||||
F 1 |
= |
|
= |
|
|
|
|
|
|
=10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(4.16) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Fx2 |
|
Pcos135 |
|
|
|
|
|
|
1 |
|
1 |
δ x2 |
|
|
||||||||||||||||||||||
|
|
|
|
−1 |
|
−1 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
−1 −1 1 |
|
|
|||||||||||||||||||
|
Psin135 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
у2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ y2 |
|
|
||||||||||||||||
Для элемента 2 аналогично получаем соотношения: |
|
||||||||||||||||||||||||||||||||||||
|
P = EAL 2 [( |
|
x2 − |
|
x3 )cos45 |
|
+ ( |
|
y2 |
− |
|
y3 )sin45 ], |
|
(4.17) |
|||||||||||||||||||||||
|
δ |
δ |
|
δ |
δ |
|
|||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Fx3 |
|
|
− Pcos45 |
|
|
|
|
|
|
|
|
|
x3 |
|
|
|||||||||||||||||||||
|
|
|
|
|
1 |
1 |
−1 |
−1 |
δ |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
1 |
−1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
e |
Fy3 |
|
− Psin45 |
|
|
5 |
− |
δ y3 |
|
|
|||||||||||||||||||||||||||
F |
2 = |
|
|
= |
|
|
|
|
|
|
|
=10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(4.18) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Fx2 |
|
|
|
|
Pcos45 |
|
|
|
|
− |
1 |
−1 |
1 |
δ x2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
−1 1 1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Fу2 |
|
|
|
Psin45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ y2 |
|
|
||||||||||||
78
60o |
R2=1000 кг с |
2 |
|
e2 |
e |
|
1 |
45o |
45o |
3 |
1 |
|
а |
y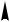
3
0
P_ 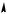 F_y2
F_y2
2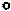
|
R2=1000 кг с |
60o |
2 |
e2 |
e1 |
45o |
45o |
1
б |
x |
|
|
|
|
_ |
|
|
Fx |
|
|
2 |
|
|
e1 |
_ |
|
|
Fy |
_ |
|
1 |
|
|
1 |
Fx |
|
1 |
|
|
|
_ |
|
|
P |
в |
|
|
Рис. 4.3
79
Для того чтобы проиллюстрировать процесс последовательного построения более четко, преобразуем уравнение (4.19) так, чтобы нумерация узлов в его матрицах подчинялась той же последовательности, что и в уравнении (4.17):
|
|
Fx2 |
|
Pcos45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
Fy2 |
|
Psin45 |
|
|
|
=10 |
5 |
|
F |
2 |
= F |
|
= |
|
|
|
|
||
|
|
x |
|
|
− Pcos45 |
|
|
|
||
|
|
1 |
|
|
|
|
|
|||
|
|
F |
|
|
|
|
|
|
|
|
|
|
у3 |
|
− Psin45 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
−1 −1 +1 |
+1 |
δ |
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
−1 −1 +1 |
+1 |
δ y |
2 |
|
. (4.19) |
|||
|
+1 +1 −1 |
|
|
|
|
|
|
|
|
|
|||||||
|
−1 |
δ x |
3 |
|
|
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
+1 +1 −1 |
−1 |
δ |
y |
3 |
|
|||
|
|
|
|
|
|
|||
Расширяя (4.17) и (4.20) до размерности системы и формируя результирующие уравнения поэлементным объединением согласно (4.11), получаем матричное уравнение:
Rx1Ry1
Rx2 =105
Ry2Rx3Ry3
Так как
|
1 |
−1 |
|
|
1 |
−1 |
||
|
|
1 |
−1 |
||
|
1 |
−1 |
|
0 |
0 |
|
0 |
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
1 0 |
0 |
δ |
x1 |
|||||
|
|
||||||||
1 |
−1 |
0 |
0 |
|
δ |
|
|||
|
y1 |
||||||||
|
|
|
|
|
|
|
|
||
2 |
0 −1 |
|
|
|
|
||||
−1 |
δ x2 |
. |
|||||||
|
|
|
|
|
|
||||
0 |
2 −1 −1 |
δ y2 |
|
||||||
−1 |
−1 |
1 |
1 |
|
|
||||
|
|
|
|
||||||
|
|||||||||
|
|
|
|
|
|||||
|
|
|
|
δ x3 |
|
||||
−1 |
−1 |
1 |
1 |
|
|
|
|
||
|
|||||||||
|
|
|
|
|
δ y3 |
|
|||
Rx |
|
=1000cos60 = 500; |
||||||||
|
2 |
= −1000sin60 = −866;, |
||||||||
Ry2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
δ x1 |
=δ y1 =δ x3 =δ x3 = 0. |
|||||||||
то уравнение (4.21) можно записать в виде
(4.20)
(4.21)
80
|
|
|
1 −1 | −1 |
|
|
|
1|0 |
|
0 |
|
0 |
|
Rx1 |
|
|
||||||||||||||||||||||
|
|
−1 |
1| 1 |
−1|0 |
0 |
|
|
0 |
|
|
|
|
|
Ry |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
|
|
|
− − − − | − − −− | − − − |
|
− − − |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
− − − |
|
|
|||||||||||||||||||||||
10 |
5 |
−1 |
1| |
|
2 |
|
|
|
0| −1 |
−1 |
|
δ x2 |
|
|
= |
|
500 |
(4.22) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
1 |
−1| |
0 |
|
|
|
|
2| −1 |
|
|
|
|
δ y2 |
|
−860 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
−1 |
|
|
||||||||||||||||||||||||||||
|
|
− − − − | − − − − | − − − |
− − − |
|
|
− − − |
|
|
|||||||||||||||||||||||||||||
|
|
|
0 0 | |
−1 |
|
−1| 1 |
1 |
|
|
0 |
|
|
|
|
|
R |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
||||
|
|
0 0 | |
−1 |
|
−1| 1 |
|
1 |
|
0 |
|
|
|
|
|
Ry3 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Разбиение матриц в (4.23), показанное штриховыми ли- |
|||||||||||||||||||||||||||||||||||||
ниями, позволяет найти |
|
х2 и |
|
у2 |
как решение системы |
|
|||||||||||||||||||||||||||||||
δ |
δ |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
x2 |
|
|
|
|
500 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
δ |
|
|
; |
|
|
|
(4.23) |
||||||||||||||||||||
|
|
|
|
|
|
105 |
0 |
2 |
|
|
|
|
= |
|
−866 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
δ |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
x2 |
= |
|
500 |
|
|
= 2,5 10−3(см); |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
δ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
т.е. |
|
|
|
|
|
|
|
|
|
|
|
2 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.24) |
||||
|
|
|
|
|
|
|
|
|
= |
|
−866 |
|
|
= −4,33 10−3(см). |
|
|
|
||||||||||||||||||||
|
|
|
|
|
δ |
у2 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подстановка равенства (4.25) в (4.23) дает следующее |
|||||||||||||||||||||||||||||||||||||
выражение для реакций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
−1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
250 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
Ry1 |
|
|
|
|
|
1−1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
(4.25) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
Rx3 |
|
|
|
|
−1−1 |
− |
433 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
отсюда |
|
|
|
|
|
|
|
|
Ry3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Rx |
= −683кгс; |
Ry |
|
= 683кгс; |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(4.26) |
|||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Rx3 |
=183кгс; |
Ry3 |
|
=183кгс. |
|
|
|
|
|||||||||||||||||||||||||
Эти результаты могут быть проверены путем использования условий равновесия фермы:
81
3 |
|
|
∑Rxi = −683+500+183= 0; |
|
|
i=1 |
(4.27) |
|
3 |
||
|
i= 683−866+183= 0.
i−1
4.2.Дискретное моделирование разъемного соединения секций трубопровода с вакуумной изоляцией∑
для транспортировки криогенных продуктов
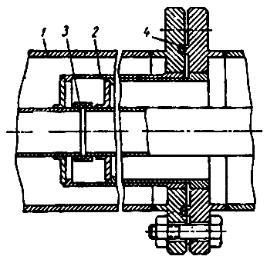
Длительно работающие трубопроводы для жидкого кислорода снабжают вакуумными видами изоляции. Трубопроводы с вакуумной изоляцией изготавливают в виде отдельных секций со своими вакуумными камерами. Для соединения секций трубопровода в конструкциях, где при разъеме возможно осевое перемещение, широко используется разъемное соединение, изображенное на рис. 4.4. Оно позволяет свести к минимуму приток тепла по металлу на концах секции, поддерживая уплотнение при температуре окружающей среды.
Рис. 4.4. Конструктивная схема соединения
82
