Все кинематические цепи делят на плоские и пространственные. В плоской кинематической цепи при закреплении одного из звеньев все остальные совершают движение в одной неподвижной плоскости или в параллельных ей плоскостях. В пространственной кинематической цепи звенья совершают движение в непараллельных плоскостях.

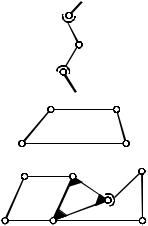
Кинематические цепи можно разделить на замкнутые и незамкнутые. Кинематическая цепь, которая не образует замкнутого контура, называется незамкнутой. Кинематическая цепь, которая образует один или несколько замкнутых контуров, называется замкнутой (рис. 1.8).

Кинематические цепи могут быть простые и сложные.

незамкнутая цепь (пространственная)

замкнутая цепь (плоская)

замкнутая цепь (пространственная)

Рис. 1.8

1.3. Структура и кинематика плоских механизмов

При кинематическом анализе и синтезе механизмов всегда необходима его кинематическая модель, такой моделью является кинематическая (структурная) схема механизма. Зная условные обозначения звеньев и кинематических пар, можно составить кинематическую (структурную) схему любого механизма.

10

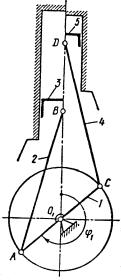
Составим кинематическую схему модели двухступенчатого двухцилиндрового воздушного компрессора (рис. 1.9). Это кинематическая схема плоского механизма.

Рис. 1.9

Если необходимо исследовать схему пространственного механизма, то чаще всего приходится делать соответствующие проекции на две или три плоскости. Схема механизма должна выполняться в масштабе. Масштабный коэффициент µe имеет размерность м/мм.

1.4. Структурная формула кинематической цепи общего вида

Если на звено не наложено никаких условий связи, то оно в пространстве имеет шесть степеней свободы. N звеньев, не соединенных кинематическими парами, имеет 6N степеней свободы или 6n независимых движений.

Соединим N звеньев парами I, II, III, IV, V классов. Пусть количество пар:

I класса = Р1,

11

II класса = Р2,

III класса = Р3,

IV класса = Р4,

V класса = Р5.

Известно, что в зависимости от класса кинематической пары на относительное движение звеньев налагается определенное число условий связи, т.е. ограничений движения. Общее число условий связи, налагаемое всеми парами будет:

5P5 + 4Р4 + 3Р3 + 2P2 +P1.

Число же степеней свободы кинематической цепи

Н = 6N – (5P5 + 4Р4 + 3Р3 + 2P2 + P1).

Если одно звено этой цепи обратим в стойку, тогда число степеней свободы всей цепи уменьшится на шесть, т.е. Н – 6 = W – число степеней свободы кинематической цепи относительно стойки.

W = 6N – 6 – (5P5 + 4Р4 + 3Р3 + 2P2 +P1);

W = 6(N – 1) – (5P5 + 4Р4 + 3Р3 + 2P2 +P1);

W = 6n – (5P5 + 4Р4 + 3Р3 + 2P2 +P1),

где W – число степеней свободы кинематической цепи относительно стойки, N – число звеньев, n – число подвижных звеньев. Это выражение было дано в 1897 году Сомовым и несколько изменено Малышевым в 1923 году, получило название

формула Сомова-Малышева для пространственной цепи.

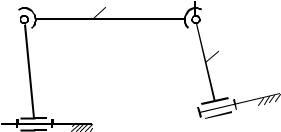
Пусть имеется пространственная кинематическая цепь из тр х звеньев, имеющая две кинематические пары 5-го класса и по одной 3-го и 4-го классов. Тогда степень свободы такой цепи W определяется следующим образом (рис. 1.10).

Таким образом, рассматриваемая кинематическая цепь имеет степень свободы относительно стойки равную единице (одно независимое движение).

Механизм представляет собой кинематическую цепь, звенья которой совершают вполне определенные движения.

12

Как же связана определенность движения звеньев механизма со степенью свободы?

3

1

D

А

n=3; P5=2; P4=1; P3=1;

W=6n – 5P5 + 4Р4 + 3Р3 + 2P2 +P1;

W=6×3–5×2–4×1–3×1=1.

Рис. 1.10

Если степень свободы W=1, это значит, что одному звену механизма можем предписать определенный закон движения, т.е. задать одну обобщенную координату, все остальные звенья будут совершать определенные движения.

Обобщенные координаты механизма – это независимые между собой координаты, определяющие положение всех звеньев механизма относительно стойки.

Звено, которому предписан определенный закон движения (задана обобщенная координата), называется начальным звеном. Часто начальное звено является входным. Число степеней свободы определяет количество начальных звеньев или обобщенных координат.

1.5. Структурная формула плоских механизмов

Для пространственного механизма степени свободы возможно определить по формуле Сомова-Малышева. Если же на движение звеньев механизма наложены общие условия связи, т.е. дополнительные требования, то это сказывается на характере движения звеньев и, следовательно, изменится структурная формула подвижности механизма.

13

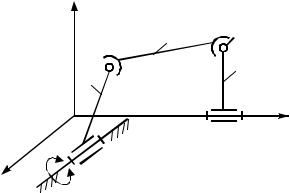
Рассмотрим механизм пространственного четырехзвен-

ника (рис. 1.11).

А

n=3; P5=2; P4=1; P3=1; W=6n – 5P5 + 4Р4 + 3Р3 + 2P2 +P1;

W=6×3–5×2–4×1–3×1=1.

Рис. 1.11

Задана одна обобщенная координата, имеем одно начальное или ведущее звено. Теперь поставим дополнительные требования – оси всех вращательных пар должны быть параллельны оси X (рис. 1.12). Это приведет к тому, что механизм обратится в плоский. Здесь невозможны три движения – вращение вокруг осей Y и Z и перемещение по X. Возможно вращение вокруг X и перемещение по Z и Y. Это обстоятельство влечет за собой изменение и структурной формулы:

W = (6 – 3) × n – (5 – 3) × P5 – (4 – 3) × Р4 = 3n – 2P5 – Р4.

Это выражение, определяющее степень свободы плоского механизма, выведено Чебышевым в 1869 году.

Применим его к рассматриваемому механизму: n=3, P5= 4, Р4=0,

W=3×3–2×4=1,

14