Проблема заключается в необходимости детального исследования напряженно-деформированного состояния конструкции соединения, обеспечивающей достаточную герметичность стыка. Использование аналитических методов не представляется возможным из-за сложности расчетной модели и характера нагружения конструкции.

Проектирование конструкции на современном уровне предусматривает использование численных методов исследования, среди которых наиболее развит метод конечных элементов.

Постановка задачи предусматривает исследование напря- женно-деформированного состояния пространственной линейноупругой конструкции разъемного соединения секций трубопровода, статически нагруженной силами внешнего атмосферного давления, силами от давления транспортируемого продукта и силами, возникающими от затяжки болтов фланцевого соединения.

При построении конечно-элементной модели использованы объемные элементы в форме призмы с треугольным основанием, пластинчатые элементы треугольной и четырехугольной формы с узлами в вершинах. Узел объемного элемента имеет 3 степени свободы: линейные перемещения вдоль осей глобальной системы координат. Каждый узел пластинчатого элемента имеет 3 линейные степени свободы вдоль трех осей локальной системы отсчета и трех угловых степеней, соответствующих поворотам вокруг этих осей. Пластинчатый элемент испытывает суперпозицию плоского напряженного состояния и изгиба.

4.2.1. Конечные элементы, используемые для моделирования конструкции разъемного соединения трубопровода

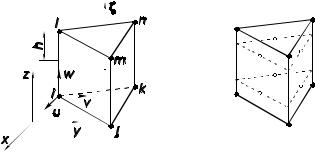
4.2.1.1. Объемный элемент в форме прямой треугольной призмы (пентаэдр)

Рассматриваемый элемент (рис. 4.5) представляет собой

прямую треугольную призму.

Целесообразность применения такого рода элементов связана с тем, что:

83

•многие детали имеют призматическую (цилиндрическую) форму или частично состоят из призматических подобластей;

•при аппроксимации пентаэдрами подобных трехмерных областей существенно упрощается проблема автоматизи-

рованной подготовки данных, возникающая, в частности, в

случае использования тетраэдров.

Рис. 4.5. Объемный элемент в форме прямой треугольной призмы:

а– геометрия, узлы и узловые перемещения;

б– расположение точек численного интегрирования

Простейший, первого порядка, пентаэдр (рис. 4.5) имеет узлы i, j, k, l, m, n,расположенные только в вершинах. Особенностью описываемого пентаэдра является то, что его нижнее и верхнее

основания параллельны плоскости xOy, а боковые ребра – оси z.

Принятый порядок локальной нумерации узлов указан на рис. 4.5: последовательность обхода узлов i, j, kнижнего треугольного основания принимается против хода часовой стрелки, если смотреть со стороны верхнего основания, а узлыl, m, nрасполагаются соответственнонад узлами i, j, k.

Функции форм прямого пентаэдра образуются путем умножения функции, интерполирующей перемещения точек в плоскости треугольного основания, на функцию, интерполирующую по третьей координате. Перемещения точек основания в его плоскости описываются с помощью L-координат, а

84

для третьей координаты z применяется линейная интерполяция с применением функций

в которых индекс i обозначает номер узла, а безразмерная ко-

и остальные коэффициенты в (4.29) получаются циклической перестановкой индексов.

Функции форм прямого пентаэдра определяются как произведения функций (4.28) и (4.29):

Интегрирование, предусмотренное для вычисления компонентов матрицы жесткости, может быть выполнено точно, однако с учетом общего численного характера конечноэлементного моделирования используется более простое и целесообразное в данном случае численное интегрирование. Применяются квадратурные формулы типа Гаусса при расположении точек интегрирования в значениях весовых коэффициентов. Соответственно принятым функциям форм прямого пентаэдра интегрирование выполняется при расположении трех точек в каждом из двух сечений (рис. 4.5).

85