
- •1. СТРУКТУРА МЕХАНИЗМОВ
- •1.2. Классификация кинематических пар
- •1.3. Структура и кинематика плоских механизмов
- •1.4. Структурная формула кинематической цепи общего вида
- •1.5. Структурная формула плоских механизмов
- •1.6. Пассивные связи и лишние степени свободы
- •1.7. Замена в плоских механизмах высших кинематических пар низшими
- •1.8. Классификация плоских механизмов
- •1.9. Структурные группы пространственных механизмов
- •2. Анализ механизмов
- •2.1. Кинематический анализ механизмов
- •2.1.1. Определение положений звеньев плоской незамкнутой кинематической цепи
- •2.1.2. Матричная форма уравнения преобразования координат точек звеньев
- •2.1.3. Определение положений, скоростей и ускорений звеньев пространственных механизмов
- •2.1.4. Графическое определение положений звеньев механизма и построение траектории
- •2.1.5. Определение скоростей и ускорений точек звеньев методом планов
- •2.1.6. Свойство планов скоростей
- •2.1.7. Построение плана скоростей и ускорений кулисного механизма (рис. 2.7)
- •2.1.8. Аналоги скоростей и ускорений
- •2.2. Силовой анализ механизмов
- •2.2.1. Условие статической определимости кинематических цепей
- •2.2.2. Силы, действующие на звенья механизма
- •2.2.3. Силы инерции звена, совершающего возвратно-поступательное движение
- •2.2.4. Силы инерции звена, совершающего вращательное движение вокруг неподвижной оси
- •2.2.5. Силы инерции звена, совершающего плоское движение (рис. 2.17)
- •2.3.1. Силовой расчет начального звена (рис. 2.18, а)
- •3. МЕХАНИЗМЫ С ВЫСШИМИ ПАРАМИ. ЗУБЧАТЫЕ МЕХАНИЗМЫ
- •3.1. Зубчатые передачи
- •3.1.1. Общие сведения. Основная теорема зацепления
- •3.1.2. Геометрические элементы зубчатых колес
- •4. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
- •4.1. Строительные конструкции
- •4.2.1. Конечные элементы, используемые для моделирования конструкции разъемного соединения трубопровода
- •4.2.1.1. Объемный элемент в форме прямой треугольной призмы (пентаэдр)
- •4.2.2. Пластинчатый элемент треугольной формы
- •4.2.3. Пластинчатый элемент четырехугольной формы
- •4.2.4. Моделирование статического состояния разъемного соединения
- •5.1. Стадии проектирования
- •5.2. Основные термины и определения
- •6. ОСИ И ВАЛЫ
- •6.1. Общие сведения
- •6.2. Проектный расчет валов и осей
- •6.2.1. Составление расчетных схем
- •6.3. Проверочные расчеты валов и осей
- •6.3.1. Расчет на выносливость валов и вращающихся осей
- •6.3.2. Расчет валов и неподвижных осей на статическую прочность
- •6.4. Проверочный расчет валов и осей на жесткость
- •7. ПОДШИПНИКИ, МУФТЫ
- •7.1. Подшипники
- •7.1.1. Подшипники скольжения
- •7.1.2. Подшипники качения
- •7.2. Муфты
- •7.2.1. Волновые передачи
- •8. Расчет простейших осесимметрично нагруженных тонкостенных оболочек вращения
- •8.1. Сферические оболочки
- •8.2. Цилиндрические оболочки (рис. 8.3)
- •9. Ременные передачи
- •9.1. Общие сведения
- •9.1.1. Классификация
- •9.1.2. Типы приводных ремней
- •9.2. Кинематические и силовые зависимости
- •9.2.1. Напряжения в ремне
- •9.2.2. Относительное скольжение ремня
- •9.2.3. Расчет передач по кривым скольжения
- •9.2.4. Допустимое полезное напряжение
- •9.2.5. Клиноременная передача
- •9.2.6. Расчет клиноременных передач
- •10. 3аклепочные соединения
- •11. Сварные соединения
- •12. Шпоночные соединения
- •13. Резьбовые соединения
- •13.1. Расчет на прочность стержня болта (винта) при различных случаях нагружения
- •13.2. Расчет соединений, включающих группу болтов
- •14. ПОРШНЕВЫЕ КОМПРЕССОРЫ И ДЕТАНДЕРЫ. МЕМБРАННЫЕ КОМПРЕССОРЫ
- •14.1. Конструкции поршневых компрессоров
- •14.2. Конструктивные схемы поршневых детандеров
- •14.3. Мембранные компрессоры
- •заключение
- •Библиографический список
3n=2Р5+Р4.
Этому условию удовлетворяют группы Ассура. Вот почему для определения реакций механизм расчленяется на группы Ассура.
2.2.2. Силы, действующие на звенья механизма
Применение метода кинетостатики предполагает использование принципа Даламбера, в связи с чем необходимо определять силы инерции звеньев механизма.
Сила инерции не является сосредоточенной силой: она распределена по всему объему звена, которое может рассматриваться как тело, состоящее из бесконечно большого числа элементарных масс, при движении которых возникают элементарные силы инерции. Для упрощения расчетов систему элементарных сил инерции приводят к главному вектору и главному моменту сил инерции и в таком виде прикладывают к звену механизма.
В плоских механизмах звенья могут совершать три вида движения: возвратно-поступательное, вращательное и сложное. Силы инерции определяются в зависимости от характера движения, совершаемого звеном.
2.2.3. Силы инерции звена, совершающего возвратно-поступательное движение
Этот вид движения характерен тем, что траектории, скорости и ускорения всех точек звена одинаковы. Рассматривая звено как неизменяемую систему одинаковых элементарных масс, каждая из которых развивает элементарную силу инерции, будем иметь систему параллельных одинаковых, направленных в одну сторону сил. Ра внодействующая таких сил по аналогии с системой элементарных сил веса будет приложена в центре тяжести звена. Эта сила будет лишь больше или меньше силы тяжести – это зависит от ускорения, с которым оно движется (рис. 2.15).
50

_ |
_ |
S |
as |
_ |
_ |
Pu= – mas |
|
P |
=mas |
||
Рис. 2.15
На этом примере легко проследить осуществление принципа Даламбера. Действительно, если звено движется поступательно с ускорением as, это значит, что на него действует не-
уравновешенная сила P = mas . Для того чтобы тело находилось в равновесии, достаточно к его центру тяжести приложить равную и противоположную силу Pu = −mas . Тогда в этот м о-
мент сумма всех сил станет равной нулю, т.е. наступает состояние равновесия.
Итак, равнодействующая сила инерции звена, движущегося поступательно, равна произведению его массы на ускорение и приложена в центре масс звена. Система сил инерции в данном случае приводится к равнодействующей.
2.2.4. Силы инерции звена, совершающего вращательное движение вокруг неподвижной оси
Применяя теорему об изменении количества движения и считая, что звено совершает поступательное движение вместе с системой координат, начало которой находится в центре тяжести звена (рис. 2.16), получим
|
|
|
= |
d ∑miVi = d mVS = −maS , |
|||||||||
Pn = − dQ |
|||||||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
dt |
|
dt |
1 |
|
|
dt |
|
|
|
||
где aS = aSτ + aSn , модуль aS найдем по теореме Пифагора.
aS = 
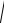 (aτS )2 +(a3n )2 = rS
(aτS )2 +(a3n )2 = rS 
 ε2 +ω4 ,
ε2 +ω4 ,
тогда модуль силы инерции
Pu = mrS 
 ε2 +ω4 .
ε2 +ω4 .
51

|
ω |
Pu’ |
|
||
|
|
|
|
|
|
ε |
|
|
|
|
|
P_u |
O |
|
_ |
||
|
|
|
y |
as |
|
|
|
|
|
_n |
_τ |
|
|
|
|
as |
|
|
|
|
|
as |
|
_ |
_ |
|
x |
||
Pu= – mas |
|
||||
|
|
|
|
_ |
_ |
|
|
|
|
Mus= – Jsε |
|
|
|
|
|
Рис. 2.16 |
|
Главный момент сил инерции относительно центра тяжести найдем по теореме об изменении кинетического момента инерции той же точки:
MuS = − ddtKS = − dtd JS ω = −JS ddtω = −JSε.
Таким образом, во вращательном движении система сил инерции при выборе центра приведения в центре тяжести приводится к главному вектору и главному моменту сил ине рции. Систему сил инерции можно представить и другой эквивалентной системой сил, выбирая за центр приведения, например, ось вращения звена, и перенося в него главный вектор сил инерции, будем иметь главный вектор, геометрически равный его прежнему значению, а складывая моменты (прежний момент и момент, получающийся в результате переноса силы из точки S в точку 0), получим главный момент сил инерции относительно нового центра приведения 0:
Muo = −JSε − PnrS = −(JSε + maSρ ρS )= −ε (JS + mr32 )= −J0ε .
52
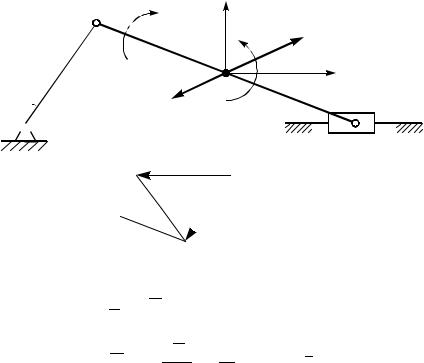
Можно найти и такой центр приведения, для которого Mи=0, т.е. такую точку, в которой приложена равнодействующая сил инерции. Такой точкой будет центр качания звена.
2.2.5. Силы инерции звена, совершающего плоское движение (рис. 2.17)
Здесь также можно найти такой центр приведения, для которого Mu=0, т.е. система сил инерции может быть сведена к равнодействующей. Как видим, только в случае поступательного движения линия действия равнодействующей сил инерции проходит через центр тяжести звена.
А |
|
y |
Mu |
ε |
|
|
|
|
|
|
S |
|
as |
|
O
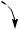 ω1
ω1
b π aBAτ  s
s 

a
Рис. 2.17
Pu = ddtQ = −maS .
MuS = − ddtKS = − dtd JSa
P_u
x
B
= −JSε .
53

2.3.Определение реакций
вкинематических парах групп Ассура
Сцелью проведения силового расчета механизм расчленяется на группы Ассура. Расчет начинается с той группы, в
состав которой входит выходное звено. Затем последовательно рассчитываются все группы, и заканчивается силовой анализ расчетом входного звена механизма. Методика расчета всех групп II класса едина.
Определение реакций в кинематических парах групп с помощью метода кинетостатики рекомендуется проводить в следующем порядке.
1.Изобразить группу Ассура в заданном положении, вычертив ее в соответствующем масштабе.
2.Приложить к звеньям группы все заданные силы и не-
известные реакции в кинематических парах.
3.Приложить к звеньям группы силы инерции и моменты сил инерции.
4.Согласно принципу отвердевания и принципу Даламбера
составить уравнение равновесия для группы в целом, как для твердого тела. Записывая уравнение равновесия для группы, следует придерживаться определенного порядка: вначале записать все силы, действующие на одно звено, затем записать все силы, действующие на другое звено. Запись уравнения следует начинать и заканчивать неизвестными реакциями. Для большей ясности в уравнение следует включать и внутренние реакции (рис. 20.4, б). Сложение векторов сил проводится в той же последовательности, в которой велась запись уравнения.
Проследим этот порядок на примере группы с тремя вращательными парами, входящей в состав шарнирного четырехзвенника. Составим уравнение равновесия группы:
R12 +G2 + Pu2 + R32 + R23 +G3 + Pu3 + Puc + R03 = 0;
известнаясторона треугольника
|
|
|
= |
|
n |
+ |
|
τ |
; |
|
|
|
= |
|
n |
+ |
|
τ . |
|
R |
|
R |
R |
|
R |
|
R |
R |
|||||||||
12 |
12 |
12 |
|
03 |
03 |
03 |
||||||||||||
54

По этому уравнению построить план сил не удастся, т.к. если построение плана свести к построению треугольника, представив все известные силы как одну сторону треугольника, то увидим, что две другие стороны включают силы, величины и направления которых не известны. Такой треугольник построить невозможно. В этом случае надо использовать уравнение равновесия моментов сил, разложив одну из реакций на два направления, пустив одну из составляющих реакции через ту точку, относительно которой будет составляться уравнение моментов. Составим уравнение моментов относительно точки B для звена 2. Выбирая точку В в качестве центра, мы исключаем тем самым из уравнения моментов нормальную составляющую R12n
реакций R12 в шарниреА и реакцию R32 в шарниреВ. Итак,
∑MB = R12τ AB + Mu2 + Pu2h2 +G2 2 = 0.
Разрешая это уравнение относительно R12τ , получим ее
величину. Направление реакции определяется ее знаком. После определения этой составляющей видим, что план сил и в этом случае построить не удается. Тогда таким же образом поступа-
ем с реакцией R03, раскладывая ее на две составляющие и составляя уравнение моментов относительно точки В для звена 3,
находимR03τ .
Рассматривая уравнение равновесия после того, как силы R12τ и R03τ отправлены в категорию известных сил, видим, что треугольник, у которого одна сторона известна по величине и направлению, а две другие (R12n и R03n ) известны по направле-
нию, построить можно. Поэтому приступаем к построению плана сил (рис. 2.18). Далее определяем реакции во внутренней паре. Для этого составляем уравнение равновесия для какоголибо одного звена (составление уравнения заключается в простом переписывании части уже составленного уравнения для группы). Напишем уравнение для звена 2, освобождая его от связей в точке В:
55
