5.2. Туннельный пробой

Туннельный пробой объясняется туннельным эффектом, то есть просачиванием электронов сквозь тонкий потенциальный барьер.

Туннельный эффект возможен в р-п переходах, имеющих своеобразную структуру. Эти переходы образованы на границе электронной и дырочной областей кристалла с большой концентрацией доноров и акцепторов в соответствующих областях. Так как концентрации примесей велики, примесные уровни расщепляются в энергетические зоны, которые из-за близости к разрешенным энергетическим зонам основных атомов кристалла сливаются с ними. Донорные уровни расщепляются в зону, перекрывающуюся с зоной проводимости в п-области кристалла, акцепторные – в зону, перекрывающуюся с валентной зоной в р-области кристалла. Ширина запрещенной зоны в результате этого уменьшается.

При слиянии примесных и основных энергетических зон уровень Ферми располагается внутри разрешенной зоны: в р-области на некотором расстоянии вниз от потолка валентной зоны, в п-области – вверх от дна зоны проводимости. В результате этого дно зоны проводимости п-области полупроводника оказывается ниже потолка валентной зоны р-области. Энергетическая диаграмма для этого случая показана на рис. 5.2.

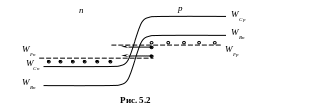При подаче обратного напряжения вследствие перекрытия энергетических зон электроны могут переходить из валентной зоны р-области в зону проводимости п-области без изменения энергии. Это явление иногда называют внутренней холодной эмиссией.

Вероятность такого перехода существует благодаря волновым свойствам электрона. Эта вероятность зависит от ширины запрещенной зоны и определяется выражением

.

Здесь π – число Пифагора; т^* – эффективная масса электрона; – ширина запрещенной зоны; h – постоянная Планка; е₀ – заряд электрона; Е – напряженность электрического поля в переходе.

Для возникновения туннельных переходов необходимо, чтобы напряженность поля в переходе достигла некоторой критической величины. Экспериментально установлено, что для германия Е_кр = 3,7·10⁵ В/см, для кремния Е_кр = 1.4·10⁶ В/см, что достижимо только в очень узких переходах, получаемых при высокой концентрации примеси.

Рассчитаем напряжение туннельного пробоя U_пр, считая, что для данного полупроводника при данной температуре критическое значение напряженности поля (при которой происходит пробой) постоянно:

Е_кр = 2U_пр / l_n.

Рассмотрим несимметричный переход, для которого N_a>>N_d. Ширина такого р-п перехода

.

Тогда .

Отсюда можно определить напряжение туннельного пробоя:

.

Таким образом, при туннельном пробое напряжение пробоя обратно пропорционально концентрации носителей заряда, то есть прямо пропорционально удельному сопротивлению полупроводника. Для практических расчетов удобнее пользоваться эмпирическими формулами:

для германия U_пр = 19000ρ_п + 9400ρ_р;

для кремния U_пр = 20000ρ_п + 7300ρ_р,

где ρ_п и ρ_р – удельные сопротивления р и п областей полупроводника, U_пр – пробивное напряжение при туннельном пробое.

Туннельный пробой при повышении температуры наступает при более низком обратном напряжении. Объясняется это тем, что с ростом температуры у полупроводников уменьшается ширина запрещенной зоны, соответственно уменьшается толщина п-р перехода и возрастает напряженность поля в переходе, что увеличивает вероятность возникновения туннельного пробоя.