Упругие волны. Волновой процесс.

Процесс распространения колебаний в сплошной среде называется волновым процессом.

Сплошная среда – непрерывно распределённая в пространстве и обладающая упругими свойствами.

Частицы среды волной не переносятся, а колеблются около своих положений равновесия, передается лишь энергия колеблющегося тела.

Волны – это изменение состояния среды, распространяющееся в ней без переноса вещества и несущее с собой энергию и импульс.

Энергия, импульс и скорость – важнейшие характеристики волн.

Основным свойством всех волн независимо от их природы, является перенос энергии без переноса вещества. В зависимости от характера упругих деформаций, возникающих при этом, различаются продольные и поперечные волны.

Продольные волны могут распространятся в средах, в которых возникают упругие силы при деформации сжатия и растяжения , т.е. в твердых, жидких и газообразных телах (рис 1а) В них частицы среды колеблются вдоль распространения волны.

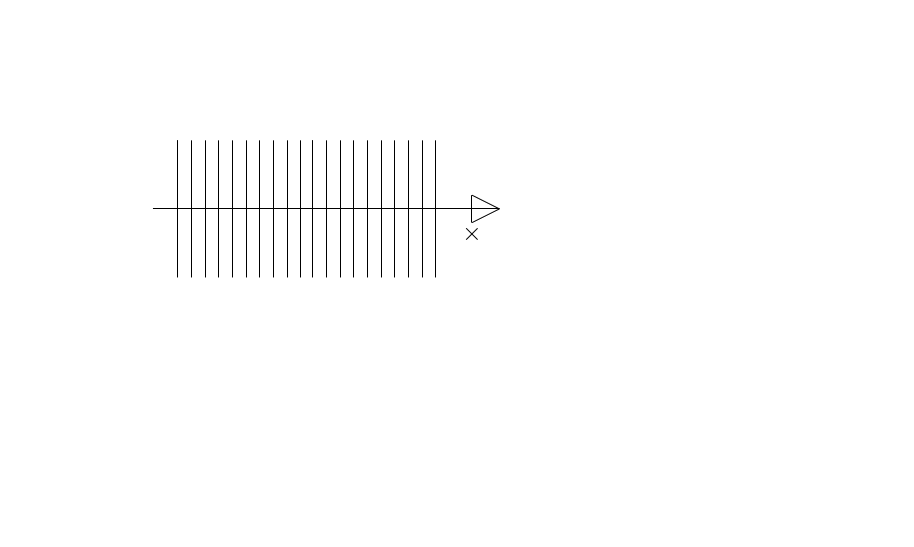
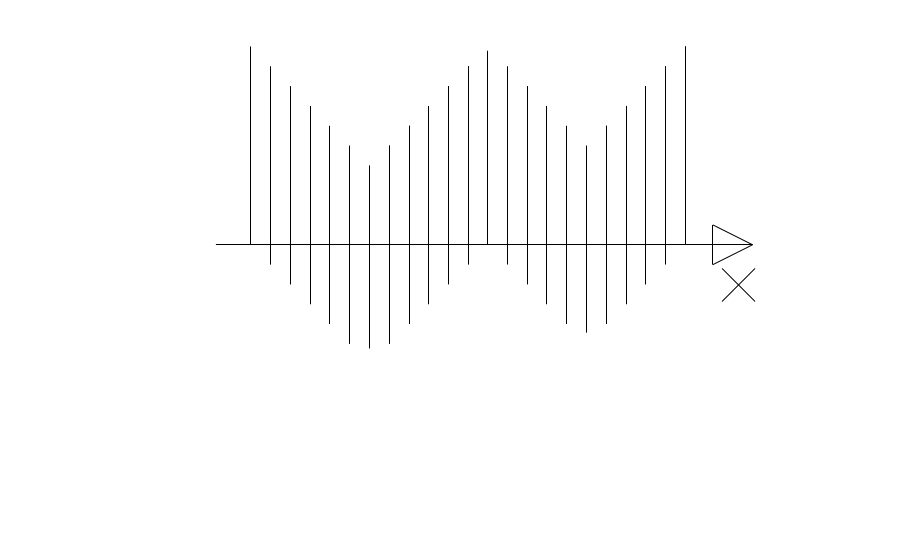Рис 1 (а) (б)

Поперечные волны могут распространяться в среде, в которой возникают упругие силы при деформации сдвига, т.е только в твердых телах. В них частицы колеблются в плоскостях, перпендикулярных направлению распространения волны.

Основные свойства волн можно изучить на простых примерах и сформулировать общие положения, которые будут справедливы для любого типа волн.

ПРИМЕР

Морские волны бьются о берега, при штормах ворочают огромные камни и переворачивают корабли.

Телецентр излучает волны мощностью в десятки тысяч ватт, малую долю которых улавливают телевизоры. Волны переносят энергию любой величины от одной точки к другой, распространяясь с конечной скоростью, зависящей от среды их расположения: так световые волны распространяются со скоростью 300 000км/с звуковые (в воздухе) – 344м/с

Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими.

Длина волны - расстояние между двумя ближайшими частицами, колеблющимися в одинаковой фазе , учитывая

λ

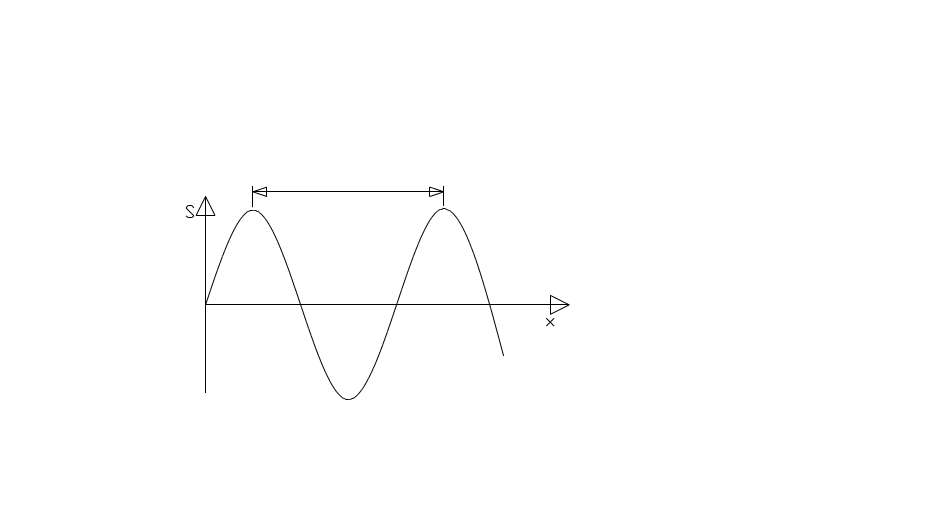
График зависимости смещения (S) всех частиц среды от расстояния до источника колебаний в данный момент времени, (график колебаний - зависимость смещений (S) данной частицы от времени).

Волна, распространяясь от источника колебаний, охватывает новые области пространства

Волновой фронт - это геометрическое место точек, до которых доходят колебания к моменту времени t. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью.

Волновой фронт в каждый момент времени один, а волновых поверхностей можно провести бесчисленное множество. Если волновые поверхности представляют собой совокупность параллельных плоскостей, то волна называется плоской, если концентрические сферы, то волна называется сферической.

Бегущими волнами называются волны, которые переносят в пространстве энергию. Количественно характеризует перенос энергии вектор плоскости потока энергии.

Уравнение плоской бегущей волны

Колебания точек описывается уравнением

X=A*sin(ωt+φ₀), где А= const - амплитуда

Источник колебаний - мембрана

φ

Чтобы пройти путь от плоскости х=0 на расстояние необходимо время . Колебания частиц в плоскости будут отставать от колебаний частиц в начальный момент времени в плоскости х=0 и описываться уравнением

, учитывая

- фаза колебаний

– скорость распространения волны, а значит и скорость распространения фазы, поэтому ее называют фазовой скоростью.

Если фазовая скорость волн в среде зависит от их частоты, то это явление называется дисперсией волн, а среда, в которой наблюдается дисперсия волн, называется диспергирующей средой.

Для характеристики волн используют волновое число К

, тогда при ( )

- уравнение плоской бегущей волны

Если волна распространяется вдоль оси х, то

В общем случае распространение волн в однородной изотропной среде описывается дифференциальным уравнением в частных производных

или , где – фазовая скорость

оператор Лапласа.

Решением является уравнение любой волны

Если среда, в которой распространяется одновременно несколько волн линейно, то применим принцип суперпозиции (наложения) волн. Исходя из принципа суперпозиции и разложения Фурье. (гармонического анализа сложного периодического колебания с частотами, кратными циклической частоте ω) любая волна может быть представлена в виде гармонических волн или в виде волнового пакета.

Скорость движения группы волн, образующих волновой пакет называется групповой скоростью