4.10.1. Барьерная емкость перехода

Плоский электронно-дырочный переход имеет две области объемного заряда: положительного в электронной области, являющегося нескомпенсированным зарядом ионов доноров и отрицательного в дырочной, являющегося нескомпенсированным зарядом ионов акцепторов. Поскольку переход обладает высоким удельным сопротивлением, то можно считать, что его электрические свойства близки к свойствам диэлектрика.

Таким образом, электронно-дырочный переход можно рассматривать как систему, состоящую из двух проводящих плоскостей, заряды которых численно равны, противоположны по знаку и разделены средой со свойствами, близкими к диэлектрику, то есть как плоский конденсатор. Тогда можно сказать, что р-п переход обладает некоторой емкостью, которая называется барьерной или зарядной.

Если изменять напряжение, приложенное к электронно-дырочному переходу, то пространственный заряд р-п перехода будет изменять свою величину, что опять же можно трактовать как проявление некоторой емкости.

Барьерная емкость р-п перехода определяется отношением изменения пространственного заряда ΔQ_пр к вызвавшему его изменению напряжения ΔU:

.

Величину барьерной емкости можно рассчитать по формуле емкости плоского конденсатора:

,

где ε – относительная диэлектрическая проницаемость материала;

ε₀ – диэлектрическая постоянная вакуума;

S – площадь обкладок конденсатора;

d – расстояние между обкладками.

Применяя эту формулу к р-п переходу, под S будем подразумевать поперечное сечение кристалла полупроводника, а вместо расстояния между обкладками возьмем толщину перехода

.

Для несимметричного перехода при условии, что концентрация акцепторов значительно превышает концентрацию доноров,

.

В случае симметричного перехода, когда концентрации доноров и акцепторов в р- и п-областях одного порядка величины, формула барьерной емкости приобретает следующий вид:

.

Барьерная емкость зависит от удельного сопротивления и подвижности носителей заряда, от толщины и площади перехода, от напряжения на нем.

Увеличение обратного напряжения расширяет область пространственного заряда, что приводит к уменьшению барьерной емкости. При прямом напряжении толщина перехода уменьшается и емкость возрастает. Барьерная емкость увеличивается с ростом концентрации примесей N_а и N_d.

Х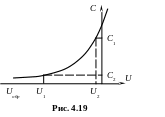 арактер зависимости С _бар = f(U_обр) показан на рис. 4.19.

Барьерная емкость р-п перехода используется в варикапах – диодах, применяемых в качестве конденсаторов переменной емкости.

4.10.2. Диффузионная емкость перехода

Если приложить к переходу прямое напряжение, то высота потенциального барьера понизится и некоторое количество электронов окажется в состоянии проникнуть через р-п переход в р-область, а дырок в п-область. Концентрации неравновесных носителей заряда будут изменяться по закону:

;

.

До появления этих электронов р-область была электрически нейтральна. Электроны, инжектированные в р-область, представляют собой некоторый отрицательный объемный заряд. Так как никакое перераспределение свободных зарядов внутри электрически нейтрального полупроводника не может скомпенсировать объемного заряда электронов, то для восстановления состояния электрической нейтральности полупроводника из внешнего вывода должно войти дополнительное количество дырок.

Процесс компенсации объемного заряда неосновных неравновесных носителей объемным зарядом основных неравновесных носителей протекает исключительно быстро.

При увеличении внешнего напряжения, приложенного к p-n переходу в прямом направлении, растет концентрация инжектирован­ных носителей вблизи границ перехода, что приводит к изменению количества заря­да, обусловленного неосновны­ми носителями в p- и n-областях. Это можно рассмат­ривать как проявление неко­торой емкости. Поскольку она зависит от изменения диффузионной составляю­щей тока, ее называют диф­фузионной.

Диффузионная емкость определяется отношением изменения величины инжектированного заряда к изменению приложенного напряжения:

.

Можно сделать заключение, что диффузионная емкость будет проявляться при прямых токах через переход или при малых обратных токах, когда еще нельзя пренебречь диффузионным компонентом тока.

Рассчитаем величину диффузионной емкости.

Полный заряд неосновных неравновесных носителей в р-области можно получить, интегрируя Δn(х):

.

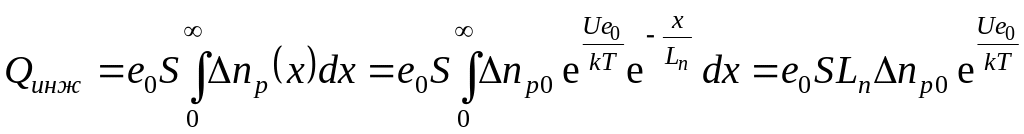Диффузионную емкость найдем, дифференцируя инжектированный заряд по напряжению:

. (4.10)

Проводя аналогичные рассуждения для инжектированных дырок, получим выражение для дырочной составляющей диффузионной емкости:

.

Воспользуемся выражением для плотности тока перехода:

. Отсюда .

Подставляя последнее выражение в уравнение (4.10) и умножая числитель и знаменатель на τ_п, получим:

.

Аналогично для дырок

.

Ток насыщения образуется неосновными носителями, возникающими на расстоянии от границы области объемного заряда, не превышающем длины диффузии L_n. Рекомбинация неосновных носителей, возникающих в точках, удаленных от области объемного заряда, на величину, превышающую L_n, происходит раньше, чем они попадут в поле области объемного заряда. Таким образом, плотность тока насыщения, представляющего собой ток проводимости, будет определяться неосновными носителями, возникающими у границы раздела (плоскости R) в параллелепипеде с площадью 1 см и длиной L_n. Величина плотности тока насыщения будет пропорциональна количеству неосновных носителей в этом объеме , скорости их возникновения и заряду единичного носителя е₀. В равновесном состоянии скорость возникновения носителей должна быть равна скорости их исчезновения. Скорость исчезновения представляет собой величину, обратную времени жизни, то есть 1/τ_n, следовательно, плотности тока насыщения для электронов и дырок определятся выражениями:

; .

С учетом этого диффузионная емкость равна

; .

Полная диффузионная емкость определяется суммой электронной и дырочной составляющей:

.

Полная емкость p-n перехода определяется сум­мой барьерной и диффузи­онной емкостей:

.

При включении p-n перехода в прямом направ­лении преобладает диффу­зионная емкость, а при включении в обратном на­правлении – барьерная.

У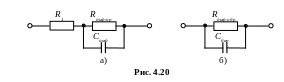 прощенные эквивалентные схемы диффузионной и барьерной емкостей перехода показаны на рис. 4.20, а,б.

Здесь R₁ – сопротивление объема р- и п-областей; R_диф.пр и R_{диф.обр} дифференциальные сопротивления р-п перехода в прямом и обратном направлении, соответственно.

При прямом включении p-n перехода С_бар << С_диф, дифференциальное сопротивление R_диф.пр мало и соизмеримо с R₁, поэтому эквивалентная схе­ма принимает вид, показанный на рис. 4.20, а. При обратном смещении

R_{диф.обр} >> R₁, С_бар >> С_диф

и эк­вивалентная схема имеет вид, показанный на рис. 4.20, б.