Теория метода

Рассмотрим более подробно явление концентрационной поляризации на капельном ртутном катоде при разряде ионов металла, например кадмия. При разряде ионов металла происходит образование амальгамы кадмия. Потенциал амальгамного электрода

Е = Е^о + ln ,

где c^(s) – концентрация ионов кадмия в растворе около электрода, с^(Ме) – концентрация амальгамы кадмия вблизи поверхности электрода.

Таким образом, чтобы найти уравнение концентрационной поляризации на капельном ртутном электроде, необходимо определить величины c^(s) и с^(Ме) в зависимости от протекающего тока. Процесс диффузии к растущей сферической поверхности значительно сложнее процесса диффузии к неподвижному твердому электроду. Так как поверхность капли непрерывно увеличивается за период ее существования и, следовательно, сила тока, текущего через каплю в раствор, растет, то вводится понятие средней за период образования капли силы тока . Как показывает точный расчет, величина среднего тока диффузии на капельном ртутном электроде

= 0,627 nFD^1/2 m^2/3 ^1/6 (c^o – c^(s) ) =  (c^o – c^(s) ) , (1)

c^o и c^(s) – концентрация ионов кадмия в объеме раствора и вблизи поверхности электрода соответственно, моль /см³;

n – число электронов, участвующих в электродной реакции;

D – коэффициент диффузии;

m – скорость вытекания ртути, мг/с;

 – период выпадения капли, с;

 – коэффициент, постоянный при данном режиме работы электрода.

Когда концентрация восстанавливающихся частиц у поверхности ртутной капли c^(s) станет равной 0, диффузионный ток будет равен предельному диффузионному току. Средний предельный ток диффузии выражается уравнением

_Д =  c^o . (2)

Уравнения (1) и (2) носят название уравнений Ильковича и используются при количественном полярографическом анализе. Из уравнений можно определить значение c^(s) :

c^(s) = ( _Д – ) . (3)

Уравнения Ильковича позволяют также определять число электронов n, участвующих в электродной реакции, коэффициенты диффузии D, делать заключение о природе лимитирующей стадии и решать другие проблемы, относящиеся к области электрохимической кинетики.

Так как на поверхности ртути образуется амальгама, то в самой капле возникает ток от поверхности в глубь капли. Величина среднего диффузионного тока внутри ртути определяется уравнением, совпадающим по форме с уравнением (1):

= 0,627 nFD_Ме^1/2 m^2/3 ^1/6 c^(Ме) = _Ме c^(Ме) , (4)

где D_Ме и c^(Ме) относятся к атомам металла, растворенного в ртути.

Подставив (3) и (4) в выражение для Е, получим выражение для концентрационной поляризации на капельном ртутном электроде (уравнение Гейровского-Ильковича):

Е = Е_1/2 + ln (5)

или для величины средней силы тока

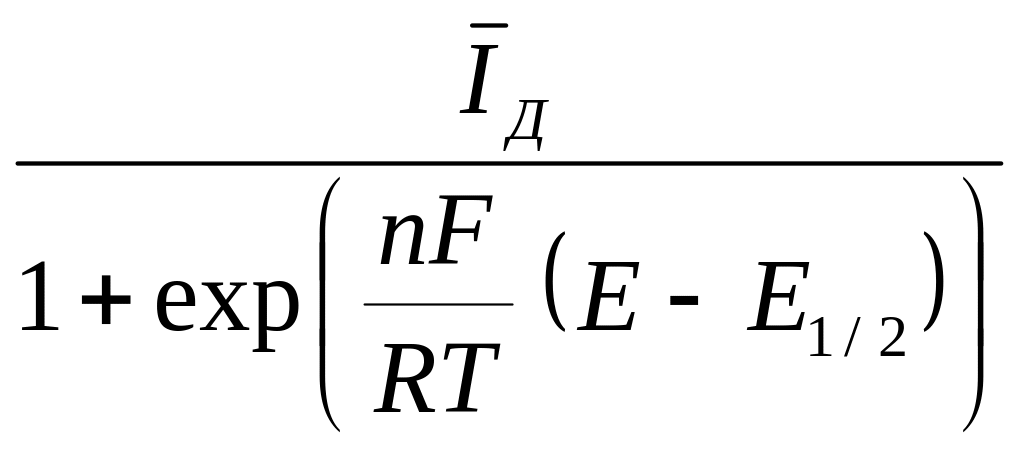= , (6)

где Е_1/2 = Е^о + ln = Е^о + ln .

Как видно, величина Е_1/2 – потенциал полуволны – зависит только от величины стандартного потенциала электрода и отношения коэффициентов диффузии атомов металла в амальгаме и ионов металла в растворе, то есть является величиной, зависящей лишь от природы реагирующего иона.