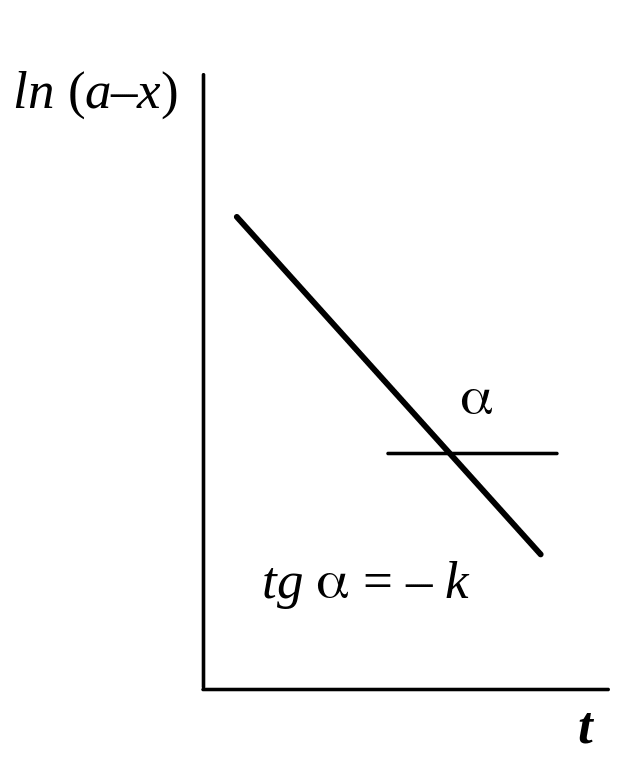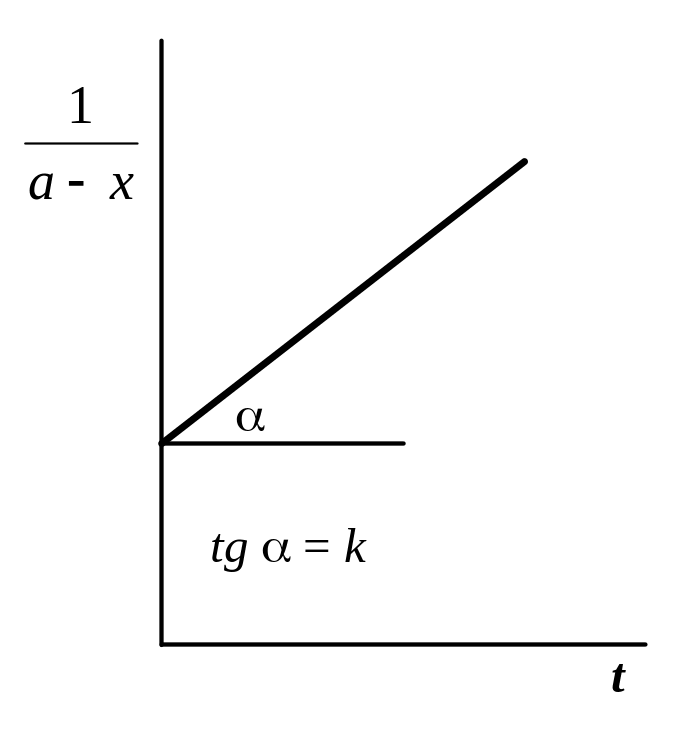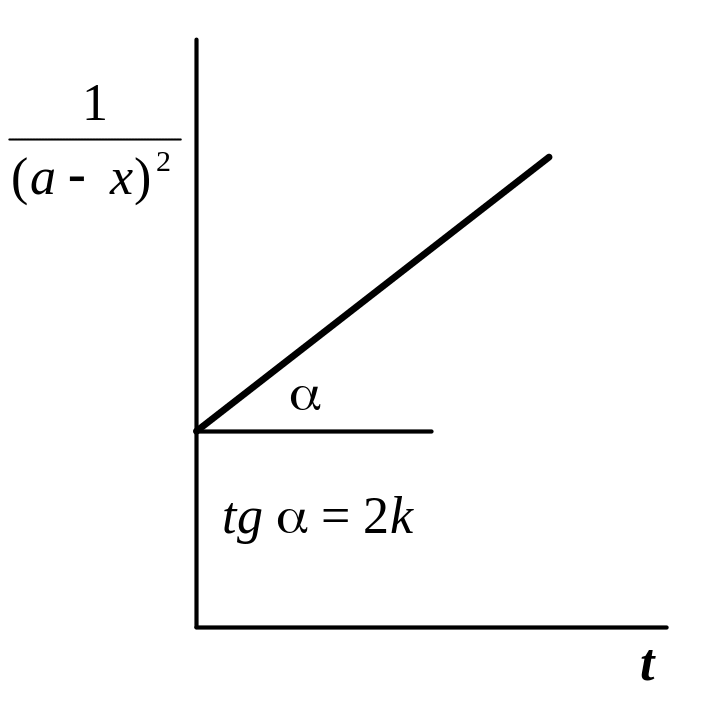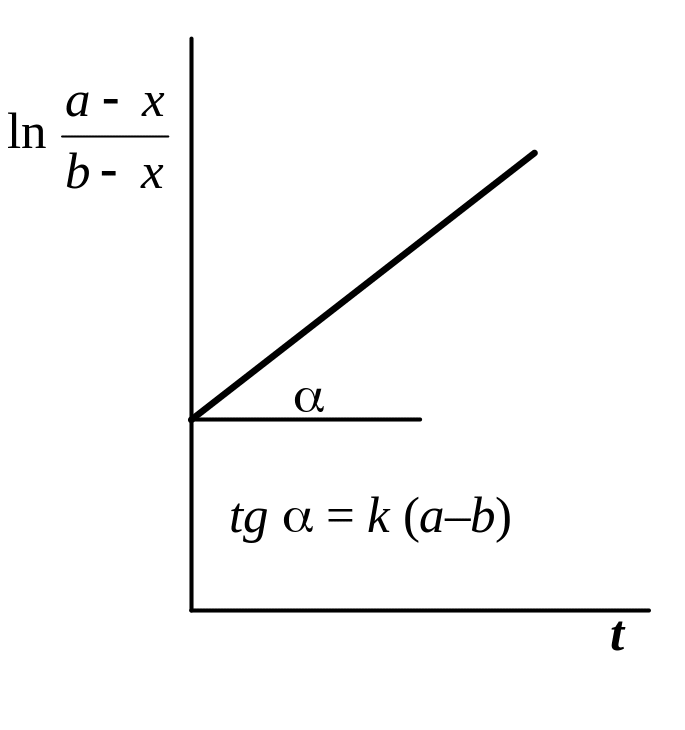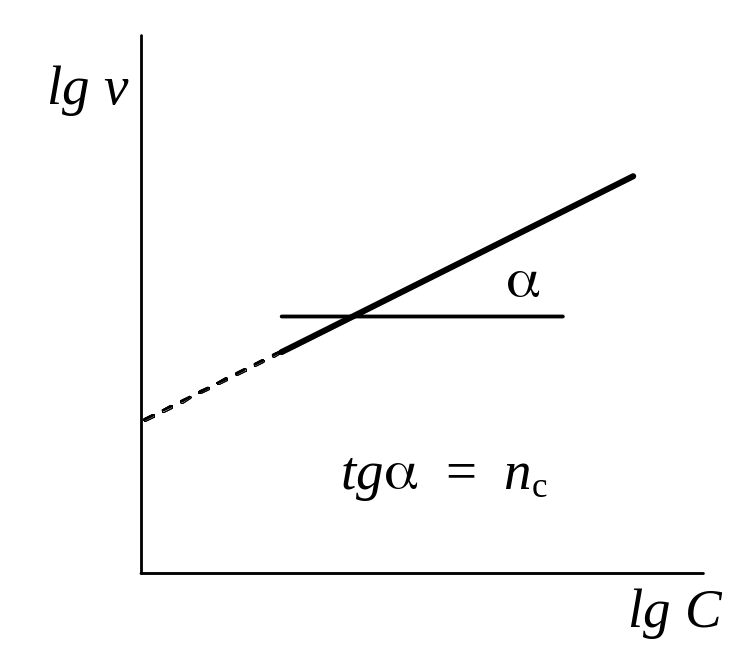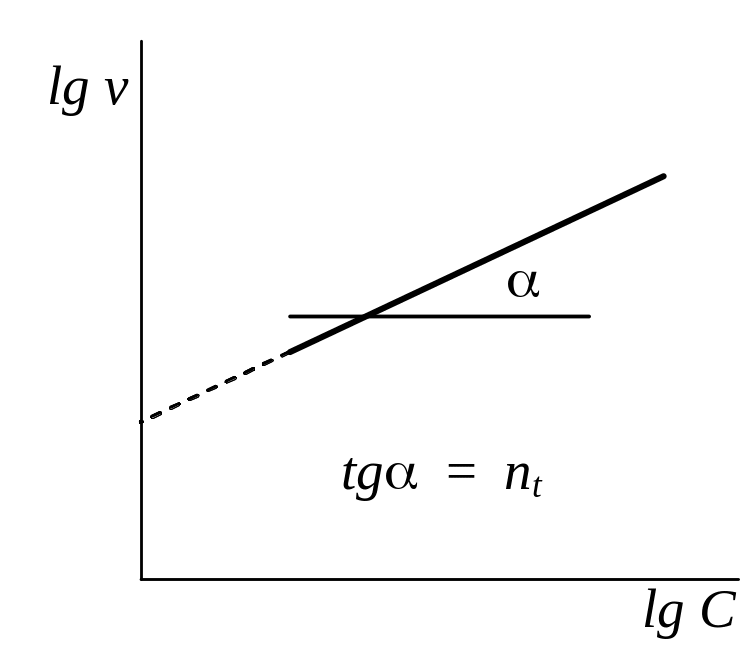- •Часть II
- •Раздел IV. Химическая кинетика и катализ
- •Двусторонние и односторонние (обратимые и необратимые) реакции
- •Кинетическая классификация реакций. Молекулярность и порядок реакций
- •Необратимые реакции первого порядка
- •Необратимые реакции второго порядка
- •Необратимые реакции n-го порядка
- •Реакции нулевого порядка
- •Сложные реакции: обратимые, параллельные, последовательные
- •Обратимые реакции первого порядка
- •В момент равновесия скорости прямой и обратной реакций одинаковы:
- •Обратимые реакции второго порядка
- •В общем виде
- •Параллельные реакции
- •Последовательные реакции
- •Методы определения порядка реакций
- •Влияние температуры на скорость реакции
- •Применение теории столкновений к бимолекулярным реакциям. Расчет константы скорости
- •Типы бимолекулярных реакций
- •Теория активного комплекса (переходного состояния)
- •Обрыв цепи
- •Длина цепи и ветви
- •Кинетика неразветвленных цепных реакций
- •Разветвленные цепные реакции
- •Тепловой взрыв
- •Сопряженные реакции
- •Основные законы фотохимии. Квантовый выход
- •Основные типы фотохимических процессов
- •Зависимость скорости фотохимических реакций от температуры
- •Мономолекулярные и тримолекулярные реакции. Реакции в растворах Мономолекулярные реакции в газовой фазе
- •Тримолекулярные реакции в газовой фазе
- •Реакции в растворах
- •Методы изучения кинетики сложных реакций
- •Общие сведения о катализе. Гомогенный катализ. Катализ кислотами и основаниями Общие сведения о катализе
- •Гомогенные каталитические реакции
- •Общая схема расчета кинетики гомогенных каталитических реакций
- •Катализ кислотами и основаниями
- •Активационный процесс в гетерогенных реакциях
- •Активированная адсорбция
- •Кинетика гетерогенных каталитических реакций
- •Истинная и кажущаяся энергия активации гетерогенных химических реакций
- •Теория активных центров в гетерогенном катализе Отравление катализатора
- •Роль поверхности и пористость катализатора
- •Связь между энергией активации и предэкспоненциальным множителем
- •Недостаточность модели однородной поверхности в катализе и адсорбции
- •Мультиплетная теория катализа
- •Теория активных ансамблей
- •Электронные представления в гетерогенном катализе
- •Раздел V. Электрохимия
- •Предмет электрохимии
- •Проводники первого и второго рода
- •Электрохимические реакции
- •Законы электролиза (законы Фарадея)
- •Теория электролитической диссоциации Аррениуса
- •Недостатки теории Аррениуса
- •Причины диссоциации. Сольватация и гидратация Теплоты сольватации (гидратации)
- •Экспериментальные теплоты гидратации ионов
- •Модельные методы расчета энергии гидратации ионов
- •Энтропия сольватации ионов
- •Состояние ионов в растворах. Число сольватации
- •Распределение ионов в растворе
- •Теория электролитов Дебая и Гюккеля
- •Сопоставление теории Дебая – Гюккеля с опытом
- •Дальнейшее развитие теории
- •Удельная и эквивалентная электропроводность
- •Влияние природы растворителя на электропроводность
- •Подвижность ионов
- •Подвижность ионов гидроксония и гидроксила
- •Связь между подвижностью ионов и их концентрацией
- •Зависимость подвижности ионов от температуры
- •Числа переноса ионов
- •Диссоциация воды. РН растворов
- •Диссоциация слабых электролитов
- •Гидролиз солей
- •Буферные растворы
- •Амфотерные электролиты
- •Произведение растворимости
- •Гальванические элементы. Эдс
- •Термодинамика гальванического элемента
- •Измерение эдс
- •Строение границы электрод-раствор. Двойной электрический слой
- •Теория конденсированного двойного слоя Гельмгольца
- •Теория диффузного двойного слоя Гуи – Чапмана
- •Адсорбционная теория Штерна
- •Дальнейшее развитие теории строения дэс
- •Электродный потенциал
- •Стандартный электродный потенциал
- •Классификация электродов
- •Электроды первого рода
- •Электроды второго рода
- •Газовые электроды
- •Амальгамные электроды
- •Окислительно-восстановительные, или редокси-электроды
- •Физические цепи
- •Концентрационные цепи
- •Химические цепи
- •Аккумуляторы
- •Определение коэффициентов активности электролитов
- •Определение рН раствора
- •Произведение растворимости
- •Потенциометрия
- •Ионоселективные электроды
- •Кинетика электрохимических процессов
- •Концентрационная поляризация
- •Электрохимическое перенапряжение
- •Напряжение разложения
- •Закономерности перенапряжения выделения водорода
- •1. Влияние плотности тока
- •2. Влияние природы металла
- •3. Влияние природы и состава раствора
- •4. Влияние температуры и некоторых других факторов
- •Теории водородного перенапряжения
- •Теория замедленной рекомбинации
- •Теория замедленного разряда
- •Электроосаждение металлов
- •Анодное растворение и пассивность металлов
- •Коррозия металлов. Борьба с коррозией
- •Кондуктометрия
- •Электроанализ и кулонометрия
- •Вольтамперометрические методы
- •Полярография. Нестационарная вольтамперометрия Классическая полярография
- •Следовательно, изменение приложенной извне разности потенциалов при выполнении измерений указанным образом равно изменению потенциала капельного электрода.
- •Теория метода
- •Твердые электроды в полярографии
- •Разновидности полярографических методов
- •Импульсная полярография
- •Осциллографическая полярография
- •Основные формулы и законы Формальная кинетика
- •Зависимость скорости реакции от температуры
- •Применение теории активных столкновений и теории активного комплекса к расчету констант скоростей реакций
- •Фотохимия
- •Ионное равновесие в растворах электролитов
- •Неравновесные явления в растворах электролитов: миграция и диффузия
- •Термодинамика гальванического элемента
- •Классификация электродов
- •Классификация электрохимических цепей
- •Аккумуляторы
- •Законы электролиза
- •Неравновесные электродные процессы
- •Оглавление
- •Физическая химия Курс лекций
- •Часть 2
- •Химическая кинетика, электрохимия
Методы определения порядка реакций
Так как стадии, через которые протекают реакции, в большинстве случаев неизвестны, предвидеть порядки реакции по каждому веществу невозможно; их следует определять специальными методами, которые будут рассмотрены ниже.
Для определения порядка реакции в целом необходимо сначала установить порядок реакции по каждому веществу, вступающему в реакцию. Сумма порядков реакции по каждому веществу дает порядок реакции в целом. Чтобы определить порядок реакции по данному веществу, необходимо создать такие условия, при которых в процессе реакции изменялась бы концентрация только этого вещества. Для этого концентрации всех остальных участников реакции должны быть настолько большими, чтобы изменением их во времени можно было пренебречь и значения этих концентраций можно было бы ввести в константу скорости (метод изолирования Оствальда). Тогда для реакции
1 A + 2 B + 3 C = 4 D + 5 E ,
протекающей при V = const, можно записать
–
![]() =
k1
=
k1
![]() , где k1
= k
, где k1
= k
![]()
![]() .
(1)
.
(1)
Все известные методы определения частных порядков реакций можно разделить на две группы: интегральные и дифференциальные.
Интегральные методы. Здесь используются кинетические уравнения для скорости реакции в интегральной форме (полученные после интегрирования дифференциального уравнения скорости реакции).
1. По времени полураспада (см. «Необратимые реакции»).
Для реакции 1-го порядка не зависит от начальной концентрации: = 0,693/ k ;
для реакции 2-го порядка обратно пропорционально начальной концентрации исходного вещества: = 1/ ka ;
для реакции 3-го порядка: = 3/(2ka 2).
В общем случае время полураспада обратно пропорционально an–1. Проводят несколько опытов с разной исходной концентрацией данного вещества. Этот метод называют иногда методом Оствальда – Нойеса; он особенно удобен для определения порядка реакций, протекающих между газообразными веществами.
2. Метод подбора уравнений, основанный на подстановке экспериментальных данных по концентрации вещества для каждого момента времени в кинетические уравнения реакций различных порядков. Определяемый порядок реакции соответствует тому уравнению, для которого при различных начальных концентрациях вещества и в различные моменты времени при заданной Т константа скорости будет оставаться постоянной.
3.
Графический
метод,
основанный на определении такой функции
концентрации, которая на графике
зависимости ее от времени дает прямую
линию. Для реакций 1-го порядка такой
функцией является ln
(a–x),
для реакций 2-го порядка –
![]() (если a
= b),
для реакций 3-го порядка –
(если a
= b),
для реакций 3-го порядка –
![]() ,
что вытекает из полученных ранее
кинетических уравнений. По наклону
полученной прямой на таком графике
вычисляют константу скорости, как это
видно из рис. 4.
,
что вытекает из полученных ранее
кинетических уравнений. По наклону
полученной прямой на таком графике
вычисляют константу скорости, как это
видно из рис. 4.
Дифференциальные методы основаны на использовании уравнения для скорости реакции в его дифференциальной форме.
1. Метод Вант-Гоффа. Проводят реакцию так, что берут все вещества, кроме одного (скажем, А) в избытке. Реакцию проводят дважды, задаваясь разными начальными значениями концентрации. Тогда можно записать два уравнения скорости
–
![]() =
k1
=
k1
![]() ; –
; –
![]() = k1
= k1
![]() .
.
Разделим уравнения друг на друга и прологарифмируем:
1-й порядок |
2-й порядок (a = b) |
|
|
ln (a – x) = ln a – kt |
=
|
|
|
3-й порядок |
2-й порядок (a b) |
|
|
|
kt
(a
– b)
=
= k (a – b) t – . |
Рис. 4. Графический метод определения порядка химической реакции |
|
![]() =
=
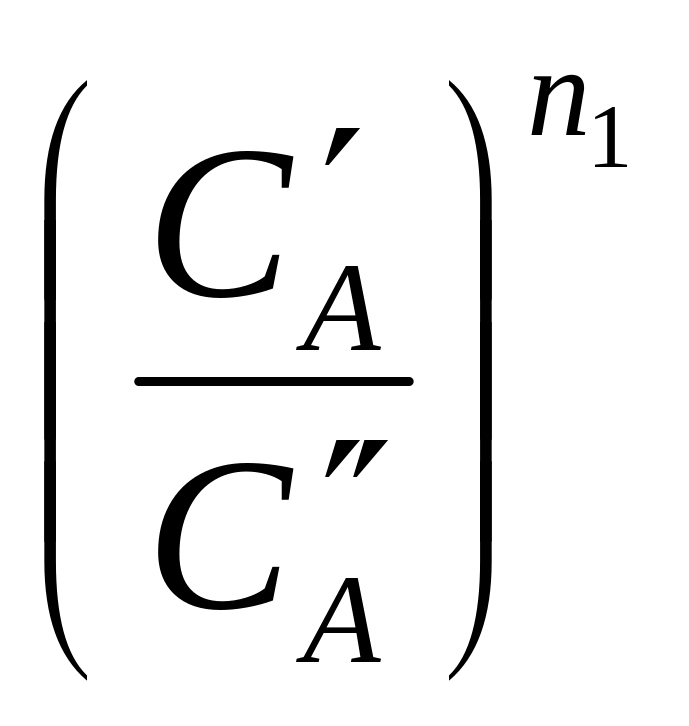 ;
;
lg (CA /t) – lg (CA /t) = n1 (lg CA – lg CA) ;
n1
=
![]() .
.
Дифференциалы заменяем конечными разностями
n1
=
![]() .
.
Это уравнение и позволяет определить порядок реакции по веществу А. Для этого надо определить изменение концентраций CA и CA за время t , задавая разные исходные концентрации вещества А, а концентрации всех остальных веществ выбирая очень большими. Значения CA и CA , входящие в знаменатель, нужно брать средними для данного промежутка времени. Аналогично определяют порядки реакций по другим веществам.
2. Графические варианты метода Вант-Гоффа основаны на использовании уравнения
v = kC n ,
которое можно преобразовать
lg v = lg k + n lgC .
На графике в координатах lg v – lgC зависимость изображается прямой линией, угловой коэффициент которой равен n. Скорость определяется тангенсом угла наклона касательной к кривой С = f (t). В зависимости от того, какая определяется скорость – в начальный момент реакции или в различные промежутки времени от начала ее – различаются два графических варианта этого метода.
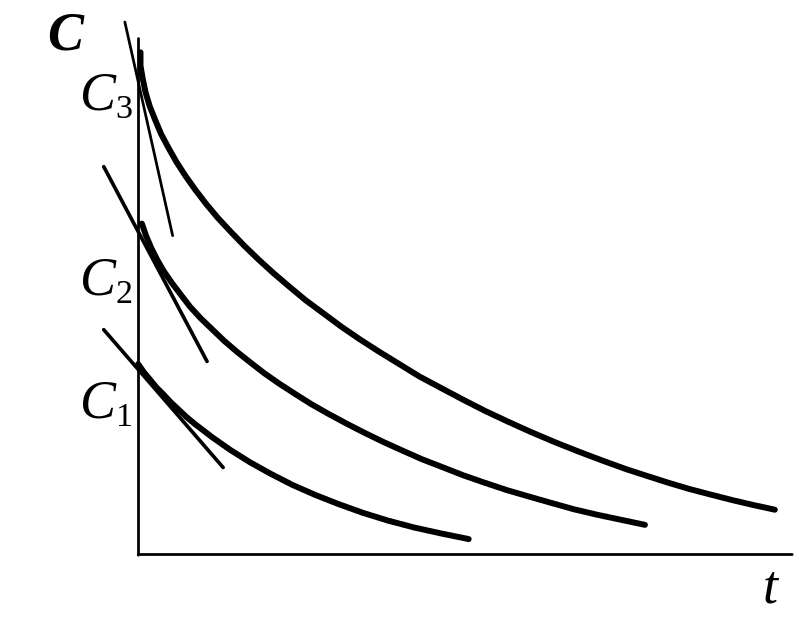
Вариант А. Определяют начальные скорости реакции при различных исходных концентрациях вещества. Для этого проводят касательную к точке кривой, соответствующей началу реакции. Логарифмы начальных скоростей наносят на график lg v = f (lgC). Наклон прямой соответствует порядку реакции nc , который называют концентрационным, или истинным (см. рис. 5). При таком определении порядка реакции образующиеся промежуточные продукты не могут влиять на ее скорость.
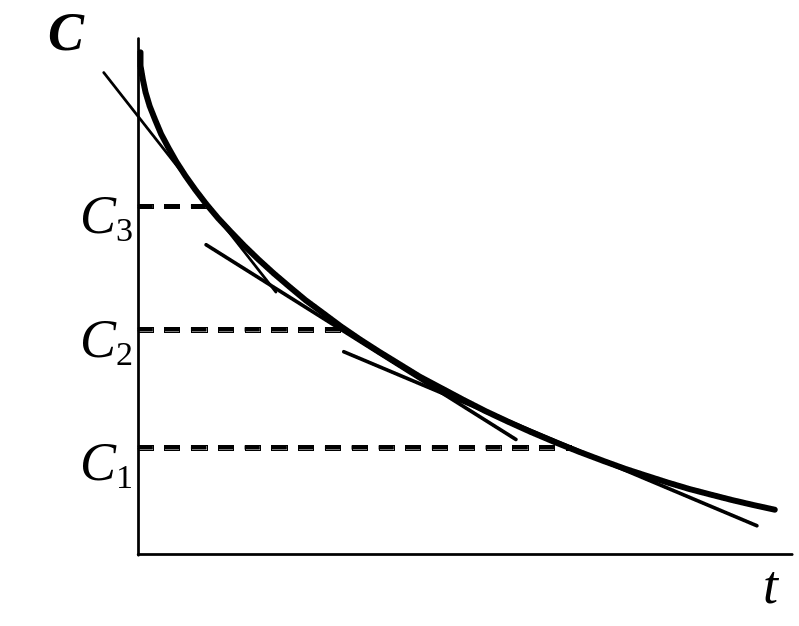
Вариант Б. Определяют скорость реакции в различные моменты времени от начала реакции, используя данные одного опыта. Для этого измеряют тангенс угла наклона касательных к кривой С = f (t) при различных значениях t. Затем строят зависимость lg v = f (lgC) , из которой находят порядок реакции, называемый временным (nt ) (рис. 6).
|
|
Рис. 5. Экспериментальное определение концентрационного (истинного) порядка реакции |
|
|
|
Рис. 6. Определение временного порядка реакции |
|
Данным способом можно обнаружить влияние промежуточных продуктов реакции на ее скорость: если промежуточные продукты искажают ход реакции, то временной и концентрационный порядки реакции могут быть разными. Кроме того, указанием на то, что реакция протекает через различные промежуточные стадии, является дробный порядок реакции.
Таким образом, необходимыми экспериментальными данными для определения порядка реакции являются данные об изменении концентрации реагирующих веществ во времени; такие данные надо получить для разных исходных концентраций веществ.