Распределение ионов в растворе

В теории электролитов очень важным является вопрос о распределении ионов в растворе. По первоначальной теории электролитической диссоциации, основанной на физической теории растворов Вант-Гоффа, считалось, что ионы в растворах находятся в состоянии беспорядочного движения  в состоянии, подобном газообразному.

Однако представление о беспорядочном распределении ионов в растворе не соответствует действительности, так как онo не учитывает электростатического взаимодействия ионов. Электрические силы проявляются на относительно больших расстояниях, и в сильных электролитах, где диссоциация велика, а концентрация ионов значительна и расстояния между ними невелики, электростатическое взаимодействие ионов настолько сильно, что оно не может не сказываться на характере их распределения. Возникает тенденция к упорядоченному распределению, аналогичному распределению ионов в ионных кристаллах, где каждый ион окружён ионами противоположного знака.

Распределение ионов будет определяться соотношением электростатической энергии и энергии хаотического движения ионов. Эти энергии сравнимы по величине, поэтому реальное распределение ионов в электролите является промежуточным между беспорядочным и упорядоченным. Около каждого иона образуется своеобразная ионная атмосфера, в которой преобладают ионы противоположного (по сравнению с центральным ионом) знака. В этом заключается своеобразие электролитов и трудности, возникающие при создании теории электролитов.

Лекция 49

Теория электролитов Дебая и Гюккеля

Основные положения современной теории растворов электролитов были сформулированы в 1923 г. Дебаем и Гюккелем. Для статистической теории электролитов исходным является следующее положение: ионы распределены в объеме раствора не хаотически, а в соответствии с законом кулоновского взаимодействия. Вокруг каждого отдельного иона существует ионная атмосфера (ионное облако)  сфера, состоящая из ионов противоположного знака. Ионы, входящие в состав сферы, непрерывно обмениваются местами с другими ионами. Все ионы раствора равноценны, каждый из них окружен ионной атмосферой, и в то же время каждый центральный ион входит в состав ионной атмосферы какого-либо другого иона. Существование ионных атмосфер и есть тот характерный признак, который, по Дебаю и Гюккелю, отличает реальные растворы электролитов от идеальных.

Энергия, связанная с ионной атмосферой, имеет электрическое происхождение, поэтому она должна быть функцией плотности электрического заряда и потенциала, создаваемого ионной атмосферой. Тепловое движение ионов в ионной атмосфере приводит к тому, что дискретные заряды этих ионов как бы размазываются. В результате ионную атмосферу, состоящую из отдельных ионов, в среднем за некоторый промежуток времени можно моделировать облаком размазанного заряда, плотность которого  уменьшается по мере удаления от центрального иона. Для связи между средней плотностью заряда  и отвечающим ему средним значением потенциала  можно использовать уравнение Пуассона

² = – ,

где ² – оператор Лапласа ² = + + .

Поскольку ионная атмосфера обладает шаровой симметрией, то уравнение Пуассона, записанное в сферической системе координат, принимает вид

+ = –

и связывает объемную плотность заряда  с потенциалом  на расстоянии r от центрального иона. В уравнение Пуассона входят две неизвестные величины:  и . Для их определения необходимо иметь второе уравнение, связывающее обе эти переменные. Дебай и Гюккель получили нужное уравнение следующим образом.

Для раствора в целом и для любого заданного его объема, достаточно большого по сравнению с размерами иона, справедливо условие электронейтральности

 n_i ez_i = 0 ,

где n_i – число ионов i-го сорта в единице объема (если выбран объем раствора, равный единице). Однако заряд некоторого элемента объема dV, находящегося вблизи какого-либо иона, будет отличаться от нуля вследствие существования ионной атмосферы. Если центральный ион, расположенный в начале координат, заряжен положительно, то элемент объема dV будет обладать избыточным отрицательным зарядом. Предполагая, что к распределению ионов в растворе применим принцип Больцмана и что силы, действующие между ионами, по своей природе электростатические, число отрицательных и число положительных ионов в элементарном объеме dV можно выразить как

dn_– = n_– dV , dn₊ = n₊ dV .

Заряд элемента объема будет равен

dV = ez_– n_– exp dV – ez₊ n₊ exp dV ,

а плотность заряда

 = ez_– n_– exp – ez₊ n₊ exp =

= e  z_i n_i exp

(учитывая, что в растворе находятся различные ионы, и приписывая z_i знак, отвечающий заряду иона). Подстановка  из этого выражения в уравнение Пуассона дает уравнение, которое в общем виде нельзя проинтегрировать. Чтобы упростить его, Дебай и Гюккель предположили, что ez_i   kT , то есть что электростатическое взаимодействие мало по сравнению с термической энергией. Разложив показательную функцию в ряд

exp = 1 – + ² + … ,

они ограничились только двумя его первыми членами, получив для  следующее уравнение:

 = e  z_i n_i –  z_i² n_i  = –  z_i² n_i 

(так как первый член правой части уравнения по условию электронейтральности равен нулю). Если ввести обозначение

 = ,

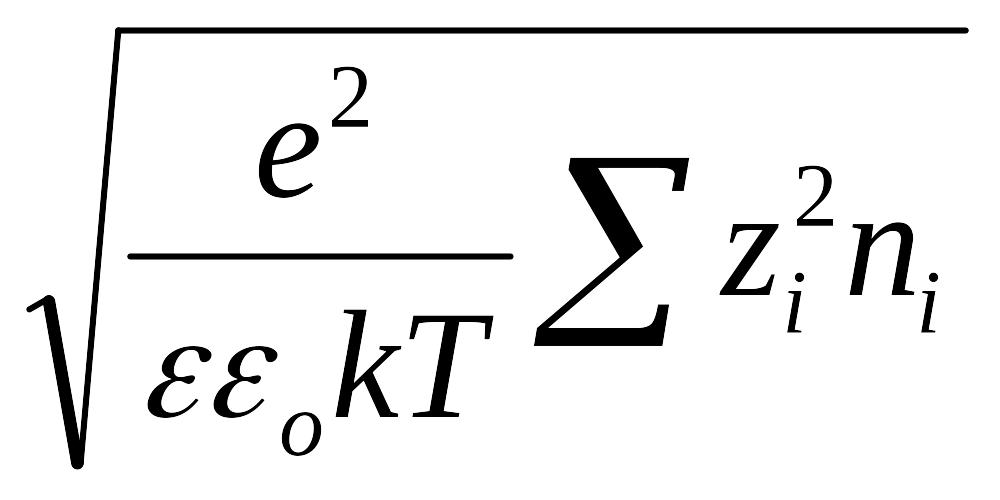то после подстановки выражения для  в уравнение Пуассона получаем дифференциальное уравнение вида

+ = ²  .

Общее решение этого уравнения второго порядка имеет вид

 = А₁ + А₂ .

Константы интегрирования А₁ и А₂ находят из пограничных условий. Как следует из основных законов электростатики, при r     0; это условие выполняется в том случае, если А₂ = 0, так как иначе с удалением от центрального иона  будет стремиться к бесконечности. Для определения А₁ в первом приближении теории Дебая – Гюккеля предполагается, что ионы можно отождествить с материальными точками, обладающими определенным зарядом. В этом случае при r  0  должен стремиться к потенциалу самого иона _i , то есть

_{r  0} = _i = ,

что является вторым пограничным условием. Если е^–r разложить в ряд, то получим

 = А₁ = А₁ (1 – r + (r)² – …) .

При r  0 всеми членами ряда можно пренебречь по сравнению с 1. Тогда

_{r  0}  _i = А₁/r , A₁ = ,  = exp (–r) .

Величина  в последнем уравнении представляет собой среднее значение потенциала в точке r, создаваемое ионной атмосферой и центральным ионом. Для вычисления ион-ионного взаимодействия представляет интерес не общий потенциал , а та его часть _а , которая создается ионной атмосферой в месте расположения центрального иона. _а называется потенциалом ионной атмосферы. Его находят по правилу суперпозиции (то есть наложения) потенциалов

_а =  – _i = (exp (–r) – 1) .

Для вычисления энергии взаимодействия необходимо определить потенциал ионной атмосферы в точке нахождения центрального иона, то есть найти предел _а при r  0. Это можно сделать, используя тот же прием – разлагая показательную функцию в ряд и пренебрегая высшими членами разложения:

lim _а =  = –  .

Величину  можно рассматривать как потенциал, создаваемый в точке нахождения центрального иона другим ионом с противоположным знаком, находящимся от центрального иона на расстоянии 1/. Величина 1/ называется характеристической длиной. Так как потенциал создается не единичным ионом, а всей ионной атмосферой, то 1/ можно отождествить с радиусом ионной атмосферы. Величину  можно рассчитать по вышеприведенному уравнению.

В первом приближении теории Дебая и Гюккеля предполагается, что энергия межионного взаимодействия имеет электростатическое происхождение. Энергия взаимодействия ионов может быть определена поэтому как энергия заряжения центрального иона в электрическом поле ионной атмосферы. Известно, что энергия заряжения частицы от 0 до заряда q в поле  равна

= = = q = ez_i (– ) =

= – 

(вместо q подставили заряд центрального иона, а вместо  – величину ).

Найдем выражение для коэффициента активности электролита. Коэффициенты активности первоначально были введены как эмпирические величины; необходимость их введения в уравнения для идеальных систем обусловлена различием между реальными и идеальными растворами. Коэффициенты активности не зависят от метода их определения и при заданных условиях и составе будут иметь одно и то же значение для любых типов равновесия. Таблицы, в которых приведены эмпирические коэффициенты активности, представляют большую ценность. В то же время в пределах теории Льюиса коэффициенты активности оказываются лишь формальными поправочными множителями, не связанными непосредственно с природой растворов и не поддающимися теоретическим расчетам.

Реальные растворы отличаются от идеальных энергией взаимодействия образующими их частиц. Сопоставление выражений для химических потенциалов частиц в реальных растворах

_i = _i^o + RT ln N_i + RT ln _i

и в идеальных растворах

= _i^o + RT ln N_i

показывает, что

RT ln _i = _i – = _i .

Таким образом, коэффициент активности отражает изменение энергетического состояния ионов, обусловленное межионным (межчастичным) взаимодействием. Расчет взаимодействия, а следовательно, и коэффициента активности возможен, если известны структура раствора и природа сил взаимодействия между образующими его частицами. Ни то, ни другое не известно с достаточной степенью точности, поэтому для решения проблемы приходится прибегать к некоторым предположениям и создавать модели растворов электролитов.

По модели Дебая и Гюккеля, энергия взаимодействия иона с ионной атмосферой, равная энергии заряжения, определяется выражением

_i = – N_A  .

Для коэффициента активности

ln _i = – N_A  .

Подстановка значения  приводит к

ln _i = – N_A ,

где I – ионная сила раствора, определяемая соотношением

I =  с_i z_i² .

( = = =

= ;

n_i = ион /м ³; n_i / N_A = моль / м ³; n_i /(1000N_A) = c_i  = моль/л ).

После перехода к десятичному логарифму и подстановки численных значений постоянных величин

lg _i = – 1,824610⁶ (T)^{– 3/2} z_i² .

Для данного растворителя и определенной Т можно написать

lg _i = – z_i² h .

Для среднего ионного коэффициента активности, который в отличие от коэффициента активности отдельного вида ионов определяется экспериментально, справедливо уравнение

lg _ = – z₊ z_–h . (1)

Для водных растворов при 25^оС, допуская равенство диэлектрических проницаемостей раствора и растворителя (78,54), h = 0,51. Для 1-1 зарядных электролитов

lg _ = – h = – 0,51 .