Глава 7. Анализ работы электрического следящего привода авиационной артиллерийской установки

7.1. Анализ устойчивости и точности работы электрического следящего привода при отсутствии корректирующих цепей

Исследование систем управления наводкой оружия артиллерийских установок имеет большое практическое значение не только на этапе проектирования.

Известно, что в процессе эксплуатации происходит изменение параметров отдельных элементов системы управления наводкой оружия вследствие их износа и старения. К этому необходимо добавить еще и то, что параметры однотипных элементов имеют случайный разброс вследствие технологических допусков на их изготовление. В совокупности все это ведет к изменению параметров систем и потере качества процессов наводки оружия на цель.

Изучение процессов, происходящих в СУНО при эксплуатации, дает возможность обоснованно подходить к выбору системы контролируемых параметров, к определению показателей надежности ААУ и периодичности проверки системы. Такой подход позволяет автоматизировать контроль исправности действия системы и сократить время на его выполнение.

В системе управления наводкой оружия артиллерийских установок используются два канала сельсинной связи, один из которых (точный) работает при малых углах рассогласования ( ). Прицельная стрельба ведется при работе СУНО на точном канале.

Практически все элементы СУНО в этом диапазоне углов имеют линейные или близкие к ним характеристики, связывающие входные и выходные переменные. Поэтому, поведение системы управления наводкой оружия артиллерийской установки можно описывать линейным дифференциальным уравнением с постоянными коэффициентами.

Таким образом, системы управления наводкой оружия авиационной артиллерийской установки являются стационарными линейными системами, исследование которых удобно проводить с использованием передаточных функций.

М атематическую модель точного канала электрического следящего привода при отсутствии корректирующих цепей (т.н. нестабилизированный электрический следящий привод) получим, если конструктивные элементы привода (см. гл.6) заменим их передаточными функциями. Математическая модель электрического следящего привода (рисунок 7.1) содержит: сельсинную связь с коэффициентом усиления ; фазочувствительный усилитель с коэффициентом усиления ; электромашинный усилитель, передаточная функция которого обычно представляется инерционным звеном с коэффициентом усиления и постоянной времени ; исполнительный электродвигатель передаточная функция которого представляет совокупность идеального интегрирующего и инерционного звена с коэффициентом усиления и постоянной времени . Входные и выходные величины для каждого звена представлены на схеме, а именно: – угловая координата оружия, т.е. регулируемый (управляемый) сигнал; – угловая координата визирной линии прицельной станции, т.е. управляющий сигнал; сигнал рассогласования; u_с, u_у, u_а – напряжения сельсинной связи, ФЧУ, ЭМУ соответственно.

Основными характеристиками систем управления наводкой оружия являются устойчивость и точность работы, время переходного процесса и др. Для анализа этих характеристик необходимо получить уравнение рассогласования системы.

Передаточная функция разомкнутой системы имеет следующий вид

(7.1)

где – общий коэффициент усиления или добротность системы.

Для исследования устойчивости и точности СУНО необходимо записать поведение сигнала рассогласования и его значение при различных параметрах движения визирного устройства. Поведение сигнала рассогласования описывается дифференциальным уравнением наиболее просто с использованием передаточной функции.

Передаточная функция замкнутого следящего привода определяется выражением

,

где – передаточная функция ООС.

Используя уравнение (7.1), получим

. (7.2)

Передаточная функция для сигнала рассогласования для такого привода определяется выражением

.

Тогда с учетом уравнения (7.1) будем иметь следующее выражение

.

Отсюда уравнение рассогласования имеет вид

(7.3)

где введем следующие обозначения:

С учетом обозначений, введенных в уравнении (7.3), получим

. (7.4)

Тип ошибки (статическая, кинематическая, динамическая) будет определяться по начальным условиям. При будет определяться статическая ошибка . При будет определяться кинематическая ошибка . При будет определяться динамическая ошибка .

Правая часть уравнения (7.4) содержит только члены, пропорциональные производной от угла , и не содержит самого угла, т.е. коэффициент , потому что рассматриваемая система содержит одно интегрирующее звено, и, следовательно, является астатической системой первого порядка или рассматриваемый ЭСП обладает астатизмом первого порядка, т.е .

Решение уравнения (7.4) состоит из общего решения однородного линейного уравнения – и частного решения уравнения с правой частью – .

Общее решение однородного линейного уравнения характеризует работу системы под действием возмущений и не нулевых начальных условий. Это решение, другими словами, является характеристикой переходного процесса и определяет устойчивость системы.

Аналитически критерий устойчивости работы автоматической системы записывается в виде:

где – некоторое заранее заданное значение.

Из уравнения (7.4) однородное линейное уравнение для рассматриваемого случая запишется в следующем виде

(7.5)

В автоматике это уравнение получило специальное название – характеристическое уравнение.

В общем случае решение уравнения имеет вид

, (7.6)

где – постоянные интегрирования, определяемые начальными условиями;

– корни, характеристического уравнения.

Решение (7.5) уравнения будет удовлетворять критерию устойчивости только в том случае, если все корни характеристического уравнения являются отрицательными. Значения зависят только от параметров рассматриваемой системы, а именно коэффициентов усиления и постоянных времени. Следовательно, меняя значения этих параметров, можно изменять значение корней характеристического уравнения.

Заметим, что с точки зрения устойчивости автоматические системы (АС) подразделяются: на структурно-устойчивые (СУАС) и структурно-неустойчивые системы (СНАС).

Устойчивость СУАС зависит только от значений параметров автоматической системы, а именно коэффициентов усиления и постоянных времени. Изменением этих параметров можно добиться устойчивости систем, не изменяя при этом структуры самой системы.

Устойчивость СНАС может быть достигнута только изменением структуры самой системы. Изменением же одних значений параметров устойчивости системы добиться невозможно.

Признаком структурно-неустойчивой АС является равенство нулю одного из коэффициентов характеристического уравнения.

Как видно, рассматриваемая на рисунке 7.1 система управления наводкой оружия является структурно-устойчивой.

Судить об устойчивости автоматической системы можно и без вычисления корней Z_i уравнения (7.5). Для этих целей существуют т.н. алгебраические критерии устойчивости, одним из которых является критерий устойчивости Раусса-Гурвица, который с успехом может применяться к линейным дифференциальным уравнениям до пятого порядка включительно.

Исследуем устойчивость нестабилизированного привода с помощью критерия Раусса-Гурвица. Для уравнения третьего порядка (7.5) таблица коэффициентов Гурвица записывается в виде матрицы следующим образом

. (7.7)

Для структурно-устойчивой АС необходимым условием устойчивости является положительность всех коэффициентов характеристического уравнения т.е. , а достаточным условием устойчивости – положительность всех определителей, полученных из матрицы (7.7).

Раскрывая определители Гурвица, получаем следующие неравенства

Отсюда следует, что условие устойчивости Раусса-Гурвица для системы третьего порядка сводится к тому, что при положительных коэффициентах характеристического уравнения должно выполняться неравенство

(7.8)

или .

Граничные условия определяются равенством

. (7.9)

Коэффициент k соответствующий граничным условиям (7.9) называется критическим коэффициентом устойчивости или критической добротностью .

Тогда

. (7.10)

В

21. Изд. №9872

следствие того, что на практике постоянные времени ЭМУ, исполнительного двигателя изменять в широком диапазоне не удается (Т_а=0,03…0,1 с; Т_дв=0,04…0,1 с), удовлетворить неравенство (7.8) проще всего путем изменения коэффициента усиления k. Для этого достаточно, например, увеличить коэффициент усиления сервоусилителя путем введения нескольких каскадов усиления.

Решая частное уравнение (7.4) с правой частью в виде , найдем выражение для кинематической ошибки

.

Тогда в лучшем случае К_кр=78 1/с. При этом кинематическая ошибка достигает величины

.

Рассматриваемый электрический следящий привод авиационной артиллерийской установки, структурная схема которого представлена на рисунке 7.1, представляет собой астатическую систему первого порядка, имеющую уравнение рассогласования третьего порядка

,

где =А(t) входной сигнал.

Согласно этому уравнению в правой части имеются члены пропорциональные производимым от угла начиная с первой производной и нет, пропорциональных самому углу . Порядок высших производных в левой и правой частях уравнения совпадает.

С учетом сказанного

.

Для получения решения в общем случае полагаем

Тогда полученное выше уравнение запишется в виде:

. (7.11)

Исходя из вида правой части уравнения рассогласования, частное решение его будем искать в таком же виде, что и возмущающие воздействие, т.е. в виде квадратичной функции времени

(7.12)

где – неизвестные пока коэффициенты.

Частное решение должно удовлетворять уравнению рассогласования. Для получения этого решения значение и его производных необходимо подставить в уравнение рассогласования. Запишем выражения производных от ошибки системы (7.12):

(7.13)

Подставляем (7.13) в левую часть (7.11), получим

Приравнивая коэффициенты при равных степенях t в левой и правой частях этого равенства получим:

Из этих условий определим неизвестные коэффициенты:

П

21*

одставляем полученные значения коэффициентов в уравнение (7.12), получаем выражение для ошибки, справедливое для следящего привода, обладающего астатизмом первого и более высокого порядка:

или

(7.14)

Это уравнение определяет ошибку привода после окончания переходного процесса при внешнем возмущении в виде угловой скорости визирного устройства и углового ускорения визирного устройства.

С учетом того, что , т.е. рассогласование в каждый момент времени складывается из величины, пропорциональной значению угловой скорости, и величины пропорциональной угловому ускорению, этого уравнение перепишется в виде

(7.15)

Подставим в уравнение (7.15) значение коэффициентов окончательно получим выражение для рассогласования при равноускоренном движении нестабилизированного следящего привода

(7.16)

Эта формула показывает, что при заданных значениях угловой скорости и углового ускорения ошибка данной системы определяется величиной коэффициента усиления.

Рассматриваемый следящий привод устойчив, пока его добротность меньше, чем критическое значение. Так, например, если взять: и , то критическая добротность будет ровна: . Такой привод будет обладать, если даже допустить, что его добротность доведена до критической величины, недопустимо большим для артиллерийских установок рассогласованием в установившемся движении, т.е. кинематическая ошибка. Действительно, уже при вращении прицельной станции со скоростью, равной , ошибка достигает величины

,

при нулевой угловой скорости вращения оружия.

Фактически критическая добротность реального привода будет ниже, чем вычисленная по выражению (7.10), из-за влияния ряда факторов, неучтенных при выводе уравнения системы. Кроме того, привод должен обладать определенным запасом устойчивости. Следовательно, ошибка нестабилизированного следящего привода больше вычисленной и может достигать значения в несколько градусов.

Возможности повышения критической добротности за счет уменьшения постоянных времени ЭМУ и двигателя весьма ограничены.

Теперь определим динамическую точность наведения следящего привода при реальных значениях , получим

.

Таким образом, с учетом запаса устойчивости системы динамическая ошибка будет еще больше. Такие ошибки нестабилизированного следящего привода для системы управления наводкой оружия ААУ неприемлемы, с точки зрения эффективности боевого применения. Уменьшение можно добиться лишь путем увеличения коэффициента усиления свыше его критического значения. Но при этом будет нарушено условие устойчивости системы, система будет неустойчивой. По этим причинам следящий привод артиллерийской установки обязательно должен содержать стабилизирующие (корректирующие) цепи.

В качестве стабилизирующих цепей используются отрицательные обратные связи по производной от напряжения на якоре исполнительного двигателя (изодромная обратная связь от напряжения на якоре двигателя), по производной от скорости оружия (изодромная обратная связь от скорости оружия), корректирующая цепь по производной от угла рассогласования и различные сочетания перечисленных цепей.

7.2. Анализ работы

электрического следящего привода

с обратной связью по производной от напряжения

на якоре исполнительного двигателя

К орректирующая цепь этого типа получила наиболее широкое применение в ЭСП. Она осуществляется с помощью электрического контура, построенного на базе пассивных линейных элементов: – резистора R и потенциометра C. Схема такого контура представлена на рисунке 7.2.

Передаточная функция контура RC определяется выражением

где – постоянная времени стабилизирующей цепи.

Из выражения для передаточной функции цепи RC следует, что дифференцирование контуром RC связано с искажениями, которые тем больше, чем больше Т. Эта цепь является отрицательной обратной связью. Звенья, поведение которых описывается передаточной функцией такого вида, иногда называют изодромными.

Структурная схема следящего привода с обратной связью по производной от напряжения на якоре исполнительного двигателя представлена на рисунке 7.3.

Сначала найдем передаточную функцию внутреннего контура, охваченного изодромной или гибкой обратной связью. Как известно, передаточная функция участка системы, охваченного отрицательной обратной связью (ООС), выражается формулой

(7.17)

где – передаточная функция участка системы, охваченного обратной связью.

Произведя преобразования, получаем

. (7.18)

Передаточная функция разомкнутого следящего привода равна

.

Подставляя сюда значения , находим

. (7.19)

где – общий коэффициент усиления или добротность системы.

Передаточная функция рассогласования имеет вид

.

Тогда, подставляя сюда значение передаточной функции (7.19), найдем

. (7.20)

Вводим следующие обозначения для коэффициентов уравнения:

(7.21)

С учетом передаточной функции для сигнала рассогласования ЭСП (7.20) можно записать дифференциальное уравнение, описывающее сигнал рассогласования

(7.22)

Исследуем устойчивость работы стабилизированного привода с помощью критерия Раусса-Гурвица. Для уравнения четвертого порядка таблица коэффициентов Гурвица записывается следующим образом

Раскрывая определители Гурвица, получаем условие устойчивости

По необходимому условию устойчивости с_i>0, i=1,2,3,4. Из данных выражений видно, что для выполнения условия необходимо, чтобы , а условия требует, чтобы с₁>0, c₃>o, .

Таким образом, условие устойчивости по Гурвицу для системы четвертого порядка можно сформулировать следующим образом: система устойчива, если все коэффициенты характеристического уравнения положительны и выполняется неравенства:

(7.23)

то есть только

Для выяснения роли стабилизирующей цепи найдем зависимость критического коэффициента усиления системы от постоянной времени Т. С этой целью подставим в неравенство (7.23) значения тех из коэффициентов (7.21) которые содержат k и произведем предельный переход, т.е. неравенство (7.23) заменим на равенство, а k заменим на К_кр в результате будем иметь:

(7.24)

Решая это квадратное уравнение, получим

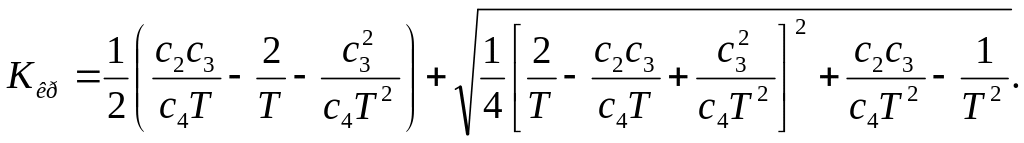(7.25)

Перед радикалом необходимо ставить только знак «+» на том основании, что физический смысл для реальной системы имеет лишь положительное значение коэффициента усиления.

Зависимость (7.25) максимально возможного коэффициента усиления (добротности) устойчивого привода от постоянной времени стабилизирующей цепи довольно сложна, так как каждый из входящих сюда коэффициентов с₂, с₃, с₄, в свою очередь зависит от Т. По этой причине характер зависимости обычно просматривается для конкретного числового примера.

Зададимся следующими величинами параметров следящего привода: – это совместный коэффициент усиления звеньев, охваченных стабилизирующей цепью. Вычисленная при этих значениях зависимость К_кр(Т) изображена на рисунке 7.4.

З аштрихованная область является областью устойчивости привода в плоскости параметров (К, Т). Из анализа зависимости можно сделать следующие выводы относительно свойств изодромной обратной связи от напряжения на якоре исполнительного двигателя:

1. Обратная связь при малых значениях ее постоянной времени несколько понижает устойчивость привода в сравнении с устойчивостью нестабилизированного привода. В рассматриваемом выше примере критическая добротность привода без гибкой обратной связи Введение обратной связи, например, с постоянной времени стабилизирующей цепи Т=0,03с понижает добротность привода до значения К_кр=20 1/с. Это объясняется тем, что при малом Т передаточная функция контура RC

приближается к передаточной функции идеального дифференцирующего звена W(p)=Tp.

2. Увеличение постоянной времени Т дает быстрый рост критический добротности привод. Так при Т=0,15с критическая добротность привода уже достигает значения

При дальнейшем увеличении постоянной времени Т добротность увеличивается, асимптотически приближаясь к некоторому предельному значению К_пр. Найдем это значение. Для этого подставим значения и найдем lim . После проведения указанных операций, получим

. (7.26)

Увеличение постоянной времени Т приближает гибкую обратную связь к жесткой. В пределе, при , изодромная обратная связь превращается в жесткую отрицательную обратную связь, так как .

На этом основании можно получить выражение для предельной добротности более коротким путем, как критическую добротность следящего привода, в котором усилитель и ЭМУ охвачены жесткой отрицательной обратной связью.

Из сопоставления (7.26) и (7.10) видно, что рассматриваемая обратная связь дает большие возможности повышения добротности привода при условии, что добротность увеличивается за счет коэффициентов усиления звеньев, охваченных стабилизирующей целью. Так, при принятом в настоящем примере значении k_уk_а=4 предельная добротность равна К_пр=550 1/с.

При анализе устойчивости ЭСП использовался критерий Раусса-Гурвица. Недостатком данного критерия является то, что он определяет лишь граничные условия устойчивости автоматической системы, т.е. определяет лишь качественную сторону, не давая ответа на вопрос о запасе устойчивости. Более наглядное представление о количественном изменении запаса устойчивости системы при изменении ее параметров дают частные методы исследования, которые являются графоаналитическими и удобны для инженерных расчетов. Далее, используя частные передаточные функции, рассмотрим критерий Найквиста, который позволяет судить о запасе устойчивости автоматической системы по частным характеристикам разомкнутой системы.

Критерий устойчивости Найквиста формируется следующим образом: если разомкнутая система устойчива (или нейтральна), то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика (АФХ) разомкнутой системы не охватывала точку на комплексной плоскости с координатами (-1; j0).

На практике иногда бывает удобным воспользоваться так называемой обратной АФХ, которая представляет собой годограф вектора изображающего на комплексной плоскости обратную частотную передаточную функцию при изменении частоты f от 0 до .

В этом случае для устойчивости замкнутой системы необходимо и достаточно, чтобы обратная АФХ разомкнутой системы охватывала точку на комплексной плоскости с координатами (-1;j0).

Рассмотрим изменение обратной АФХ при переходе от нестабилизированного ЭСП к стабилизированному приводу. На основании формул (7.1) и (7.19) запишем обратные частотные передаточные функции разомкнутых систем.

Для нестабилизированного привода имеем

. (7.27)

Для стабилизированного привода аналогичным путем получаем

. (7.28)

Умножив числитель и знаменатель дроби на разность 1-Tjf и затем приводя полученную комплексную величину к нормальному виду и учитывая что первое слагаемое, представляет собой обратную АФХ привода без гибкой ООС, окончательно получим АФХ для стабилизированного привода

.(7.29)

П олученное выражение показывает, что введение в схему следящего привода стабилизирующей обратной связи деформирует обратную АФХ системы. Каждая точка характеристики (рисунок 7.5) смещается влево вдоль действительной оси и вверх или вниз вдоль мнимой оси в зависимости от знака разности Т-Т_дв. При достаточно большом Т характеристика охватывает точку – 1 на действительной оси и следящий привод при этом превращается из неустойчивого в устойчивый.

Качественную картину влияния стабилизирующей цепи на устойчивость привода можно проследить также с помощью логарифмической амплитудной и фазовой частотной характеристик.

Существенной характеристикой действия стабилизирующей цепи является ее влияние на точность следящего привода. В первую очередь представляет интерес вопрос о влияние угла рассогласования на типовых режимах работы привода, а именно, при установившемся движении с постоянной скоростью и при движении с постоянным ускорением.

Как указывалась ранее, типовой электрический следящий привод артиллерийской установки представляет собой астатическую систему первого порядка. Введение в такую схему изодромной обратной связи не изменяет порядка астатизма. Это видно из выражения передаточной функции (7.19), которая содержит в знаменателе множитель p в первой степени. Соответственно этому, уравнение рассогласования (7.22) имеет в правой части члены, пропорциональные производным от угла , начиная с первой производной, и не имеет члена пропорционального самому углу.

При вращении визирного устройства с постоянной угловой скоростью, равной , процесс слежения оружия за визирным устройством приобретает установившийся характер, что дает основание в уравнении (7.22) положить равным нулю все производные от угла рассогласования. Уравнение приобретает вид .

Подставляя сюда значения коэффициентов, получаем формулу для определения величины угла рассогласования , совпадающей с формулой для нестабилизированного следящего привода, обладающего равной добротностью.

Следовательно, изодромная обратная связь от напряжения на якоре исполнительного двигателя не оказывает никакого влияния на точность следящего привода в установившемся движении с постоянной скоростью. Такой вывод может быть сделан непосредственно из рассмотрения физической картины работы привода. При вращении оружия с постоянной угловой скоростью напряжение на щетках двигателя остается постоянным и в стабилизирующей цепи, содержащей конденсатор, ток не протекает. Стабилизирующая цепь не участвует в работе привода, но она резко увеличивает К.

Теперь проведем анализ равноускоренного режима работы, т.е. при вращении визирного устройства с постоянным ускорением. После подстановки в равенство (7.15) значений коэффициентов (7.21) получим выражение для рассогласования при равноускоренном движении в приводе с изодромной обратной связью от напряжения на якоре исполнительного двигателя

(7.30)

Аналогично выражение было получено для нестабилизированного ЭСП

,

где второе слагаемое возникает из-за инерционности системы, обусловливающей запаздывание оружия при ускоренном движении визирного устройства.

Сопоставляя выражения (7.30) и (7.16), находим, что стабилизирующая цепь создает для стабилизированного привода дополнительную ошибку, равную .

Объясняется это тем, что возрастающее напряжение на якоре исполнительного двигателя вызывает ток зарядки конденсатора стабилизирующей цепи. Напряжение, создаваемое изодромной обратной связью, вычитается из напряжения сельсинной связи. Однако, ошибка стабилизированного привода будет всегда меньше, чем у нестабилизированного, так как введение стабилизирующей цепи дает возможность во много раз увеличить добротность системы.