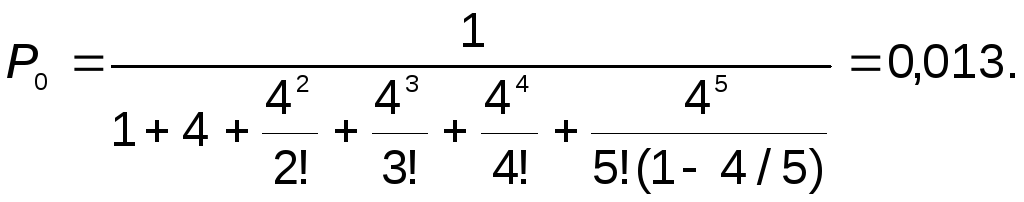Тема 13. Модели массового обслуживания

Многие экономические задачи связаны с системами массового обслуживания (СМО), т.е. такими системами, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо услуг, а с другой стороны, происходит удовлетворение этих запросов. СМО включает в себя следующие элементы: источник требований, входящий поток требований, очередь, обслуживающее устройство (канал обслуживания), выходящий поток требований. Исследованием таких систем занимается теория массового обслуживания.

Теория массового обслуживания первоначально возникла для оценки будущего поведения (прогнозирования) состояний систем телефонной связи. Телефонные станции должны обслуживать клиентов по случайно возникающим потребностям.

Первыми наиболее серьезными публикациями, которые по праву считаются основополагающими работами по теории массового обслуживания, были труды датского инженера А.К. Эрланга; его работа "Теория вероятностей и телефонные разговоры" опубликована в 1909 г. Именем Эрланга названы: исследованный им тип многоэтапных системах массового обслуживания; функция распределения вероятностей для потока требований в этих системах; формулы для определения среднего времени ожидания и других параметров эрланговых систем; единица интенсивности поступления заказов в телефонные каналы.

Крупный вклад в математическую теорию одноканальных и многоканальных систем с пуассоновым входящим потоком и произвольным временем обслуживания внесен советскими учеными, академиками А.Н. Колмогоровым и А.Я. Хичиным.

Возникшая и развивавшаяся вначале для решения проблем телефонной связи теория массового обслуживания оказалась весьма общим и мощным средством. Впоследствии она была использована для анализа и расчетов систем посадки самолетов, резервирования мест на железнодорожном и воздушном транспорте, погрузки и разгрузки судов в портах, обслуживания пациентов в клиниках, таксомоторных парках, систем обслуживания в магазинах, управления производственными потоками и т.п. Общие уравнения теории массового обслуживания, под названием уравнений размножения и гибели, используются для изучения эволюционного процесса в биологии.

Методами теории массового обслуживания в настоящее время решаются многие экономические задачи. Так, например, в области маркетинга при организации торговли эти методы позволяют определить оптимальное количество торговых точек данного профиля, численность продавцов, частоту завоза товаров и другие параметры. Другим характерным примером систем массового обслуживания могут служить склады и базы снабженческо-сбытовых организаций, и задача теории массового обслуживания сводится к тому, чтобы установить оптимальное соотношение между числом поступающих на базу требований и числом обслуживающих устройств, при котором суммарные расходы на обслуживание и убытки от простоя транспорта были бы минимальными. Теория массового обслуживания может найти применение и при расчете площади складских помещений, при этом складская площадь рассматривается как обслуживающее устройство, а прибытие транспортных средств под выгрузку – как требование.

Привести в соответствии спрос и предложение путем определения рациональной интенсивности обслуживания оказывается совсем не так уж просто, как кажется на первый взгляд, поскольку спрос, или поток требований, в подавляющем большинстве случаев оказывается случайной величиной, точное значение которой в тот или иной момент времени предсказать невозможно. Поэтому теория массового обслуживаний широко использует методы теории вероятностей.

Системы массового обслуживания (СМО) классифицируются по разным признакам.

1. В зависимости от условий ожидания требованием начала обслуживания различают:

• СМО с потерями (отказами);

• СМО с ожиданием;

• СМО с ограниченным временем ожидания.

В СМО с отказами требования, поступающие в момент, когда все каналы обслуживания заняты, получают отказ и утрачиваются. Классическим примером системы с отказами является телефонная станция. Если вызываемый абонент занят, то требование на соединение с ним получает отказ и утрачивается.

В СМО с ожиданием требование, застав все обслуживающие каналы занятыми, ставится на очередь вплоть до освобождения любого из обслуживающих каналов.

СМО, допускающие очередь, но с ограниченным числом требований в ней, называются системами с ограниченным временем ожидания.

2. По числу каналов обслуживания СМО делятся на:

• одноканальные;

• многоканальные.

3. По месту нахождения источника требований СМО делятся на:

• разомкнутые (когда источник требования находится вне системы);

• замкнутые (когда источник находится в самой системе).

Примером разомкнутой системы служит ателье по ремонту телевизоров. Здесь неисправные телевизоры являются источником требований на их обслуживание и находятся вне самой системы, их число можно считать неограниченным. К замкнутым СМО относится, например, станочный участок, в котором станки являются источником неисправностей, а следовательно, и требований на их обслуживание.

Возможны и другие признаки классификации СМО, например, по дисциплине обслуживания, однофазные и многофазные СМО и др.

Применяемые в теории массового обслуживания методы и модели условно разделимы на аналитические и имитационные.

Аналитические методы теории массового обслуживания позволяют получить характеристики системы как некоторые функции от параметров ее функционирования. Благодаря этому появляется возможность проводить качественный анализ влияния отдельных факторов на эффективность работы СМО.

В настоящее время теоретически наиболее разработаны и удобны в практический приложениях методы решения таких задач массового обслуживания, в которых поток требований является простейшим (пуассоновским).

Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, т.е. вероятность поступления за время t ровно k требований задается формулой:

(1)

Простейший поток обладает тремя основными свойствами: ординарности, стационарности и отсутствия последствия.

Ординарность потока означает практическую невозможность одновременного поступления 2-х и более требований. Например, достаточно малой является вероятность того, что в группе станков, обслуживаемых бригадой ремонтников, одновременно выйдут из строя несколько станков.

Стационарным называется поток, для которого математическое ожидание числа требований, поступающих в систему в единицу времени (обозначим ), не меняется во времени. Таким образом, вероятность поступления в систему определенного количества требований в течение заданного промежутка времени t зависит от его величины и не зависит от начала его отсчета на оси времени.

Отсутствие последствий означает что число требований, поступивших в систему до момента t, не определяет того, сколько требований поступит в систему за время t+t.

Например, если на ткацком станке в данный момент произошел обрыв нити и он устранен ткачихой, то это не влияет на возможность нового обрыва на данном станке в следующий момент и тем более на вероятность возникновения обрыва на других станках.

Важной характеристикой СМО является время обслуживания требований в системе. Время обслуживания является, как правило, случайной величиной и, следовательно, может быть описано законом распределения. Наибольшее распространение в теории и особенно в практических приложениях получил экспоненциальный закон. Функция распределения имеет вид:

(2)

Вероятность того, что время обслуживания не превосходит некоторой величины t, определяется формулой (2), где  - параметр экспоненциального закона распределения времени обслуживания требований в системе, т.е. величина, обратная среднему времени обслуживания:

(3)

Рассмотрим аналитические модели наиболее распространенных СМО с ожиданием, т.е. таких СМО, в которых требования, поступившие в момент, когда все обслуживающие каналы заняты, ставятся на очередь и обслуживаются по мере освобождения каналов.

Общая постановка задачи:

Система состоит из n обслуживающих каналов. Каждый из них может одновременно обслуживать только одно требование.

В систему поступает простейший (пуассоновский) поток требований с параметром . Если в момент поступления очередного требования в системе на обслуживании уже находится не меньше n требований (т.е. все каналы заняты), то это требование ставится на очередь и ждет начала обслуживания.

Время обслуживания каждого требования t_обсл является случайной величиной, которая подчиняется экспоненциальному закону распределения с параметром .

Как уже говорилось выше, СМО с ожиданием можно разбить на две большие группы: замкнутые и разомкнутые. К замкнутым относятся системы, в которых поступающий поток требований ограничен. Например, мастер, задачей которого является наладка станков в цехе, должен периодически их обслуживать. Каждый налаженный станок становится в будущем потенциальным источником требований на наладку. В подобных системах общее число циркулирующих требований конечно и чаще всего постоянно.

Если питающий источник обладает бесконечным количеством требований, то системы называются разомкнутыми. Примерами подобных систем могут служить магазины, кассы вокзалов, портов и др. Для этих систем поступающий поток требований можно считать неограниченным.

Отмеченные особенности функционирования каждой из этих двух видов систем накладывают свой оттенок на используемый математический аппарат. Расчет характеристик работы СМО различного вида может быть проведен на основе расчета вероятностей состояний СМО (так называемые формулы Эрланга).

Рассмотрим алгоритм расчета показателей качества функционирования разомкнутой системы массового обслуживания.

При изучении таких систем рассчитывают различные показатели эффективности обслуживающей системы. В качестве основных показателей могут быть вероятность того, что все каналы свободны или заняты, математическое ожидание длины очереди (средняя длина очереди), коэффициенты занятости и простоя каналов обслуживания и др.

Введем в рассмотрение параметр . Заметим, что если , то очередь не может расти безгранично. Это условие имеет следующий смысл:  - среднее число требований, поступающих за единицу времени, - среднее время обслуживания одним каналом одного требования, поэтому - среднее число каналов, которое необходимо иметь, чтобы обслуживать в единицу времени все поступившие требования.

1. Вероятность того, что все обслуживающие каналы свободны:

(4)

2. Вероятность того, что занято точно k обслуживающих каналов, при условии, что общее число требований, находящихся на обслуживании, не превосходит числа обслуживающих аппаратов:

при 1kn

(5)

3. Вероятность того, что в системе находится k требований, в случае, когда их число больше числа обслуживающих каналов:

при kn

(6)

4. Вероятность того, что все обслуживающие каналы заняты:

(7)

5. Среднее время ожидания требованием начала обслуживания в системе:

(8)

6. Средняя длина очереди:

;

(9)

или

7. Среднее число свободных от обслуживания каналов:

(10)

8. Коэффициент простоя каналов:

(11)

9. Среднее число занятых обслуживанием каналов:

(12)

10. Коэффициент загрузки каналов:

(13)

Рассмотрим конкретный пример. Пусть фирма по ремонту различной аппаратуры имеет n=5 опытных мастеров. В среднем в течение рабочего дня от населения поступает в ремонт =10 радиоаппаратов. Общее число радиоаппаратов, находящихся в эксплуатации у населения, очень велико, и они независимо друг от друга в различное время выходят из строя. Поэтому есть все основания полагать, что поток заявок на ремонт аппаратуры является случайным, пуассоновским. В свою очередь, каждый аппарат в зависимости от характера неисправности также требует различного (случайного) времени на ремонт. Время на проведение ремонта зависит во многом от серьезности полученного повреждения, квалификации мастера и множества других причин. Пусть статистика показала, что в среднем в течение рабочего дня каждый из мастеров успевает отремонтировать =2,5 радиоаппарата. Требуется оценить характеристики работы фирмы по ремонту радиоаппаратуры.

1. Определим параметр системы :

Так как <n, то очередь не может расти безгранично (фирма справляется с входящим потоком требований на ремонт аппаратуры).

2. Вероятность того, что все мастера свободны от ремонта аппаратуры равна (формула 4):

3. Вероятность того, что все мастера заняты ремонтом (7):

Это означает, что 55,4% времени мастера полностью загружены работой.

4. Среднее время обслуживания каждым каналом одного аппарата:

(результат получен при условии семичасового рабочего дня).

5. В среднем время ожидания каждым неисправным аппаратом начала ремонта равно (8):

6. Очень важной характеристикой является средняя длина очереди, которая определяет необходимое место для хранения аппаратуры, требующей ремонта (9):

аппарата

7. Определим среднее число мастеров, свободных от работы (10):

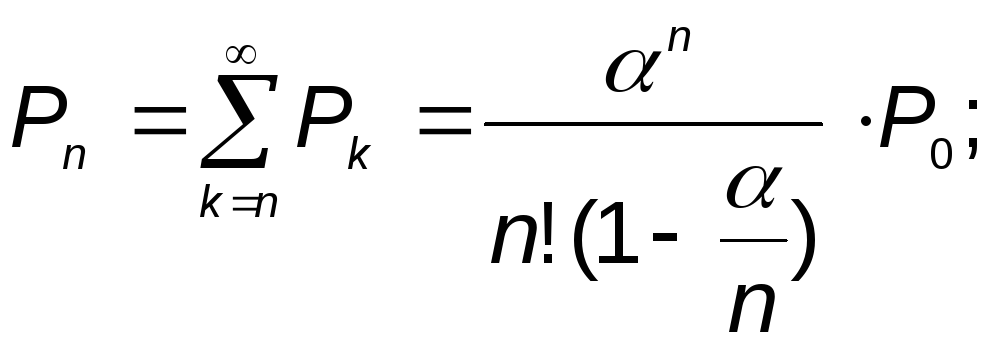
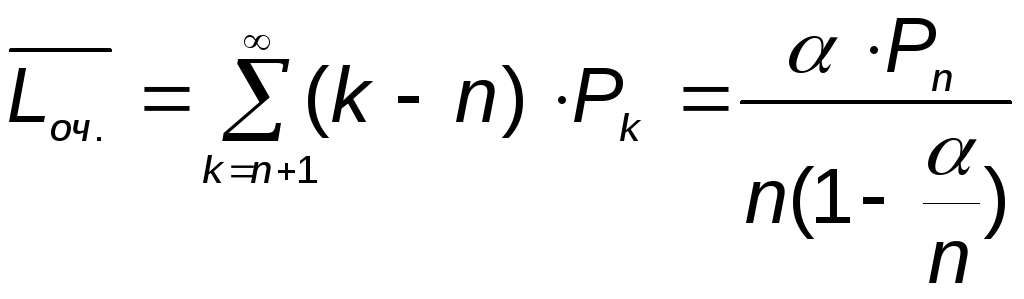мастера.