Тема 9. Модели и методы динамического программирования

9.1. Моделирование процессов наилучшего распределения ресурсов методом динамического программирования

Основные идеи, приведшие к созданию метода динамического программирования, развиты американским ученым Беллманом в начале 1950-х годов.

В задачах динамического программирования процесс принятия решений распадается на ряд последовательных этапов, что дает возможность принять ряд последовательных решений, обеспечивающих оптимальность развития экономического процесса в целом. В результате строится такая вычислительная схема, согласно которой решение сложной многовариантной задачи заменяется многократным решением относительно простой задачи, что позволяет значительно сократить объем вычислений.

Представим себе некоторый процесс, распадающийся на несколько этапов, например производство на предприятии в течение ряда лет. Пусть эффективность деятельности предприятия характеризуется некоторым показателем, например получаемой прибылью. Для функционирования предприятия в каждый из годов t = 1, ..., n используется некоторый ресурс (например, капиталовложения), причем потребление этого ресурса за n лет не должно превысить заданную величину S.

Известно, что при выделении ресурса в количестве х_t в год предприятие получает прибыль в размере .

Покажем возможные распределения ресурса и получаемой прибыли по годам:

x1	x2	xt	xn
1	2	t	n

Покажем динамику получения прибыли:

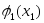
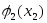
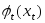
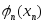
1	2	t	n

Итак, от распределения ресурса во времени существенно зависит и динамика получаемой прибыли.

Требуется так распределить ресурс S по годам рассматриваемого периода, чтобы суммарная прибыль была максимальной, т.е. необходимо найти такой неотрицательный вектор Х = (х₁, ..., х_n), при котором функция прибыли Z принимает наибольшее значение.

Математическую модель такого распределения можно записать следующим образом:

Отсюда видно, что сумма прибыли складывается из прибылей, получаемых по годам. Процесс распределения ресурса, о котором идет речь, это управляемый процесс, т.е. мы может выбирать параметры х_t, которые влияют как на получение прибыли в каждом году, так и на общую величину прибыли.

Процесс распределения, например капиталовложений, в динамике естественным образом распадается на n шагов, где t-й шаг - это выделение предприятию капиталовложений в году t.

Такую же математическую модель получим, если ресурс будет распределяться не по годам, а между n различных предприятий в одном периоде (году).

Аналогичную модель получим, если рассмотрим задачу о распределении заданного объема работ по разным видам оборудования.

В соответствии с объемом выполняемой работы могут существенно различаться и эксплуатационные расходы. Задача может состоять в таком распределении работ по видам оборудования, чтобы суммарные эксплуатационные расходы были минимальными.

Любую многошаговую задачу можно решать по-разному: или все параметры находить сразу, за один шаг, или строить оптимальное управление постепенно, шаг за шагом.

Обычно второй способ значительно проще, особенно при большом числе шагов.

Идея последовательной оптимизации и составляет суть метода динамического программирования.

Нельзя считать пошаговой или последовательной оптимизацией то, что вся задача разбивается на ряд малых, которые решаются отдельно и независимо друг от друга.

Решение, принимаемое на одном шаге, должно быть дальновидным, учитывающим все последствия, к которым оно может привести в будущем.

Только на последнем шаге решение может быть принято без прогноза на будущее. На последнем шаге метода динамического программирования оптимизация означает максимальную эффективность только одного этого шага.

Проиллюстрируем идею метода динамического моделирования на примере задачи оптимального распределения ресурсов.

Рассмотрим следующую ситуацию.

Объединение располагает финансовыми средствами в 5 млн. руб., которые оно намерено использовать для реконструкции и модернизации четырех своих предприятий. В зависимости от величины используемых капиталовложений предприятие ежегодно получает прирост прибыли в размерах, показанных таблице:

Таблица исходных данных

Капиталовложения (млн. руб.)	Прирост прибыли (млн. руб.)
0	0	0	0	0
1	0,28	0,25	0,15	0,20
2	0,45	0,41	0,25	0,33
3	0,65	0,55	0,40	0,42
4	0,78	0,65	0,50	0,48
5	0,90	0,75	0,62	0,53

Здесь - прирост прибыли, полученный на k-м предприятии при величине капиталовложений х_k. Эти функции заданы в табличной форме.

Требуется так распределить капиталовложения между предприятиями, чтобы прирост прибыли был наибольшим.

Тогда математическая модель задачи запишется так:

Целевая функция Z(x₁, x₂, x₃, x₄) выражает общий ежегодный прирост прибыли объединения, соответствующий распределению капиталовложений между четырьмя предприятиями Х=(x₁, x₂, x₃, x₄).

1. Обозначим через f₁(S)=max максимальный прирост прибыли при , который может быть получен на первом предприятии в случае выделения ему S единиц капиталовложений. Так как все функции монотонно возрастают, ясно, что прирост прибыли будет наибольшим, если предприятие освоит все выделенные ему капиталовложения. Поэтому можно записать, что:

(1)

2. Пусть теперь S млн. руб. капиталовложений распределяются между первым и вторым предприятиями, т.е. капиталовложения должны быть разделены на две части (х₂; S-x₂), где х₂ - капиталовложения, выделяемые второму предприятию, а S-x₂ - остающаяся для первого предприятия часть.

В результате такого распределения прирост прибыли на первом предприятии составит величину f₁(S-x₂), на втором - , а общий прирост будет равен f₁(S-x₂)+ .

Будем выбирать величину х₂ таким образом, чтобы общий прирост прибыли на 1-м и 2-м предприятиях был наибольшим.

Обозначим через f₂(S) получаемый при выборе х₂ максимальный прирост прибыли на обоих предприятиях, т.е.

f2(S)=(+f1(S-x2))

(2)

Отметим, что задача (2) является однопараметрической задачей (задачей максимизации, зависящей только от одной искомой переменной х₂).

Обозначим через х₂(S) величину капитальных вложений, выделяемых 2-му предприятию из S млн. руб. капиталовложений, обеспечивающую суммарный максимальный прирост прибыли на двух предприятиях.

Управление (решение) х₂(S) называется условно-оптимальным, так как оно оптимально при условии, если первым двум предприятиям выделяются капиталовложения в объеме S единиц.

Далее в соответствии с методом динамического программирования следует построить еще функции f₃(S) и f₄(S).

3. Функция f₃(S) выражает максимальный прирост прибыли, который может быть получен на трех предприятиях в случае распределения между ними S млн. руб. капиталовложений. Эта функция строится по такому же принципу, как и функция f₂(S), а именно:

f3(S)=(+f2(S-x3))

(3)

Задача (3) - это задача принятия решений на 3-м шаге, т.е. задача определения капиталовложений третьему предприятию. Эта задача решается для каждого значения S=. В результате решения определяются две величины: величина х₃(S) - условно-оптимальный объем капиталовложений, выделяемых 3-му предприятию, и f₃(S) - прирост прибыли на трех предприятиях в случае наилучшего распределения между ними S млн. руб.

4. Последней задачей в нашем примере будет задача поиска условно-оптимальных решений х₄(S) для четвертого предприятия, т.е. следующая задача максимизации:

f4(S)=(+f3(S-x4))

(4)

Уравнения (1)-(4) называются рекуррентными уравнениями Беллмана.

Задача распределения ресурса с использованием рекуррентных уравнений Беллмана решается в два этапа.

I этап. Последовательно решаются задачи (1)-(4). Результаты их решения: - можно представить в виде следующей сводной, или итоговой таблицы: