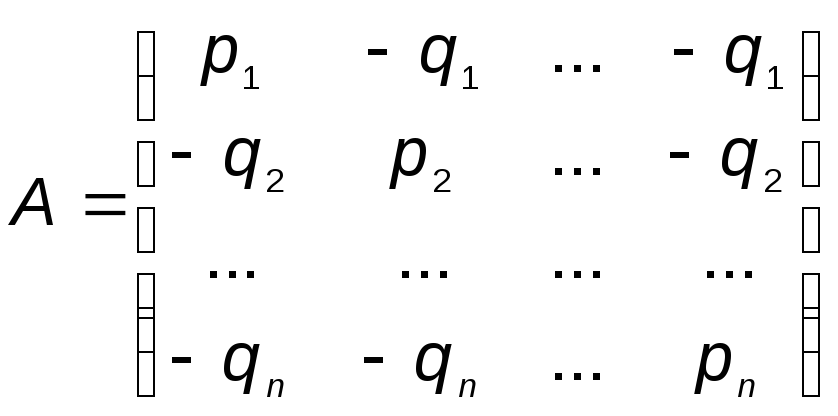10.2.Стохастическое программирование

Стохастическое программирование представляет собой совокупность методов решения оптимизационных задач вероятностного (стохастического) характера. Задача об оптимальном использовании ресурсов, транспортная задача и др. становятся задачами стохастического программирования, если параметры целевой функции либо системы ограничений (или те и другие) рассматривать как случайные величины. В стохастической постановке эти задачи будут полнее отображать экономическую действительность.

При решении стохастических задач проще всего найти средние значения всех случайных параметров и свести такие задачи к обычным, детерминированным задачам математического программирования. Однако такой подход не всегда эффективен, так как при некоторых реализациях случайных величин (параметров) можно прийти к решению, далекому от оптимального, или даже к отсутствию решений задачи.

Другой подход состоит в том, что на первом этапе устанавливается предварительный оптимальный план на основе решения детерминированной задачи, который и реализуется на этом этапе. Затем на втором (последующих) этапе этот план корректируется в соответствии с реальными статистическими характеристиками параметров. Так поступают, например, при решении задачи об оптимальном использовании ресурсов, транспортной задачи при неопределенном спросе на продукцию.

Тема 11. Модели конфликтных ситуаций в теории игр

11.1.Основные понятия теории игр

Выбор оптимальных решений может осуществляться в условиях определенности, риска и неопределенности. При выборе решений в условиях риска исследователь располагает полной статистической информацией, которой достаточно для определения вероятности допустимых решений и выбора среди них оптимального “в среднем”. В условиях неопределенности такая информация отсутствует.

Аппарат теории игр предназначен для выбора оптимальных решений в условиях неопределенности, т.е. предметом ее изучения являются ситуации, когда отсутствует полная информация, необходимая для выбора решения. Кроме того, в рассмотренных ранее задачах выбор решения осуществлялся одним лицом. В данном параграфе речь пойдет о задачах с несколькими участниками. Несовпадение целей участников процесса, их интересов создает конфликт между ними, или конфликтную ситуацию. Необходимость анализировать такие ситуации привела к возникновению теории игр. Методы теории игр разработаны применительно к специфическим конфликтным ситуациям, которые обладают свойством многократной повторяемости. Целью теории игр является выработка рекомендаций по рациональному образу действия участников многократно повторяющегося конфликта.

Первые работы по теории игр относятся к началу ХХ в. Основателем теории игр является американский математик Дж. фон Нейман, который в 1928 г. доказал основополагающую теорему теории игр - теорему о минимаксе. Бурное развитие теория игр получила после выхода в свет в 1944 г. книги Дж. фон Неймана и О. Моргенштерна “Теория игр и экономическое поведение”, в которой впервые было дано систематизированное, полное и строгое изложение теории игр. Определенную роль в этом развитии сыграло создание и совершенствование электронной вычислительной техники.

Авторы этой книги провели анализ конфликтных ситуаций, возникающих в условиях капиталистической экономики, когда при наличии свободной конкуренции в роли конфликтующих сторон выступают, например, торговые фирмы, промышленные и другие предприятия. Они надеялись, что теория игр окажет большое влияние на развитие экономических исследований. Однако в силу различных причин методы теории игр не нашли широкого применения в экономике. Одна из основных причин такого положения - математические модели экономических систем слишком сложны для анализа их с помощью методов теории игр.

Конфликтные ситуации могут возникать и во многих других областях человеческой деятельности. Это ситуации, складывающиеся при планировании и в ходе военных действий, при анализе надежности технических систем. Здесь теория игр нашла широкое применение.

В настоящее время теория игр представляет собой развитую математическую дисциплину. За последние годы были преодолены трудности, возникающие из-за сложности анализа математических моделей экономических систем методами теории игр. Созданы новые, позволяющие решать такие задачи численные методы.

Как известно, математика изучает не сами системы, а их модели. В теории игр рассматриваются модели конфликтных ситуаций. Реальные конфликтные ситуации обычно сложны, поэтому исход конфликта зависит от большого количества факторов. Чтобы сделать возможным математический анализ конфликтной ситуации, необходимо создать такую ее модель, которая бы учитывала влияние основных факторов и игнорировала второстепенные. Такая упрощенная модель называется игрой.

Итак, игра - это модель конфликтной ситуации. От реальной конфликтной ситуации игра отличается тем, что ведется по определенным правилам, которые известны участникам конфликта и строго ими выполняются. Правила определяют возможные варианты действий участников игры, объем информации об этих действиях, а также результат игры.

Базой для анализа конфликтных ситуаций послужили широко известные спортивные и азартные игры (шахматы, шашки, карточные игры). Поэтому в теории игр используется следующая терминология.

Игроки - это стороны, участвующие в конфликте. Игроками могут быть как отдельные личности, так и коллективы людей, имеющих общие цели (спортивные команды, неприятельские армии, конкурирующие фирмы, страны и т.п.).

Выигрыш (проигрыш, платеж) - результат конфликта. Предполагается, что интересы игроков поддаются количественному описанию и, следовательно, выигрыш определяется некоторым числом.

В игре могут сталкиваться интересы двух и более игроков. В первом случае игра называется парной, во втором - множественной. В дальнейшем изложении будут рассматриваться только парные игры, имеющие наибольшее практическое значение.

Различают понятия “игра” и “партия игры”. В данном случае под игрой понимают совокупность правил, определяющих поведение игроков, а под “партией игры” - реализацию игры некоторым конкретным образом от начала до конца (например, партия игры в шахматы). Как уже отмечалось, теория игр дает рекомендации по рациональному образу действия участников многократно повторяющегося конфликта. Это сводится к предположению о том, что любая игра состоит из бесконечного числа партий и оптимальное поведение игроков является оптимальным “в среднем” на множестве партий игры.

Каждая партия игры состоит из последовательности ходов. Ходом в теории игр называется выбор одного из предложенных правилами игры действий и его осуществление. Сами действия называются стратегиями (или чистыми стратегиями). Существует и понятие смешанной стратегии, которое будет определено позднее.

Для разрешения конфликтной ситуации игрокам приходится принимать решения путем выбора какой-то стратегии. Если число возможных стратегий каждого игрока конечно, то игра называется конечной, в противном случае - бесконечной.

Игры бывают одноходовые и многоходовые. При одноходовой игре каждый игрок делает по одному ходу и сразу определяется результат игры (например, игра в кости, игра в монету). Предполагается, что каждому игроку известен набор стратегий противника и результат, к которому приводит выбор определенной стратегии.

Ходы могут быть личные и случайные. Личный ход осуществляется в результате сознательного выбора игроком одной из стратегий. Например, в шахматах каждый ход является личным. Уже первый ход - это выбор одной из 20 возможных стратегий, а именно 16 ходов пешками и 4 хода конями. Случайный ход осуществляется не игроком, а некоторым случайным образом.

В игре могут сталкиваться интересы двух (игра парная) или нескольких (игра множественная) противников; существуют игры с бесконечным множеством игроков. Если во множественной игре игроки образуют коалиции, то игра называется коалиционной; если таких коалиций две, то игра сводится к парной.

На промышленных предприятиях теория игр может использоваться для выбора оптимальных решений, например, при создании рациональных запасов сырья, материалов, полуфабрикатов, когда противоборствуют две тенденции: увеличение запасов, гарантирующих бесперебойную работу производства, и сокращения запасов в целях минимизации затрат на их хранение. В сельском хозяйстве теория игр может применяться при решении таких экономических задач, как выбор для возделывания одной из возможных культур, урожай которых зависит от погоды, если известны цена единицы каждой культуры и средняя урожайность каждой культуры в зависимости от погоды (будет ли лето засушливым, нормальным или дождливым); в этом случае одним из игроков выступает сельскохозяйственное предприятие, стремящееся обеспечить наибольший доход, а другим игроком является природа.

Решение подобных задач требует полной определенности в формулировании их условий (правил игры): установления количества игроков, выявления возможных стратегий игроков, возможных выигрышей (проигрыш понимается как отрицательный выигрыш). Важным элементом в условии игровых задач является стратегия, т.е. совокупность правил, которые в зависимости от ситуации в игре определяют однозначный выбор действий данного игрока. Если в процессе игры игрок применяет попеременно несколько стратегий, то такая стратегия называется смешанной, а ее элементы называются чистыми стратегиями.

Одним из основных видов игр являются матричные игры, которые называются парными играми с нулевой суммой (один игрок выигрывает столько, сколько проигрывает другой) при условии, что каждый игрок имеет конечное число стратегий. В этом случае парная игра формально задается матрицей А (платежной матрицей).

Каждой чистой стратегии игрока I (первого игрока) ставится в соответствие строка матрицы, а чистой стратегии игрока II (второго игрока) - ее столбец. Элемент этой матрицы а_ij характеризует платеж игроку I игроком II в ситуации (i, j), т.е. когда игрок I выбрал i-ю свою стратегию, а игрок II - j-ю свою стратегию. Матрица А называется поэтому платежной матрицей игры, или матрицей выигрышей игрока I. Если элемент а_ij положителен, то он показывает выигрыш игрока I (проигрыш игрока II) в ситуации (i, j), если же элемент а_ij отрицателен, то это означает проигрыш I (выигрыш игрока II).

В качестве примера игры двух лиц с нулевой суммой рассмотрим условную военную игру под названием “игра полковника Блотто”. Две армии ведут борьбу за два населенных пункта. Армия полковника Блотто (игрок А) состоит из четырех формирований, армия противника (игрок В) - из трех.

Сформулирует правила игры. Армия, которая посылает больше формирований на один или другой пункт, занимает его и уничтожает посланные туда формирования противника, получая по единице за каждый занятый пункт и каждое уничтоженное формирование противника. В случае равенства сил на одном или другом пункте противники очков не получают. Общий выигрыш определяется как сумма выигрышей в двух пунктах.

Партия игры представляет собой упрощенную имитацию военных действий. Каждый противник должен решить, как распределить свои силы, чтобы, не зная действий противника, выиграть максимальное количество очков.

Поскольку игроки стремятся к наибольшему выигрышу, они будут использовать в бою все формирования. Следовательно, у полковника Блотто имеется пять стратегий: (4,0); (0,4); (3,1); (1,3); (2,2), а у противника - четыре стратегии: (3,0); (0,3); (2,1); (1,2). Первое число в каждой стратегии показывает количество формирований, посланных на первый пункт, второе - на второй пункт. Теперь составим платежную матрицу, которая представлена табл. 1.

Поясним расчет одного из элементов платежной матрицы, например а₅₁=-2 (игроки А и В применяют свои чистые стратегии А₅ и В₁). Игрок А посылает на первый пункт меньше формирований (два), чем игрок В (три). Согласно правилам игры игрок А теряет все свои формирования и первый пункт, проигрывая соответственно 2 и 1 очко. Выигрыш игрока А на первом пункте составит - 3 очка. На второй пункт игрок А посылает два своих формирования, а игрок В - ни одного. Следовательно, игрок А выигрывает только 1 очко, получая его за взятие второго пункта. В итоге выигрыш игрока А составит - 2 очка или, по-другому, игрок А проигрывает 2 очка, а игрок В столько же очков выигрывает.

Таблица 1

Вj Аi	3.0	0.3	2.1	1.2
4.0	4	0	2	1
0.4	0	4	1	2
3.1	1	-1	3	0
1.3	-1	1	0	3
2.2	-2	-2	2	2

Рассмотрим другой пример построения платежной матрицы - из практики маркетинговых исследований. Пусть на базе торговой фирмы имеется n типов товара ассортиментного минимума. В магазин фирмы должен быть завезен только один из этих типов товара. Если товар типа j(j=) будет пользоваться спросом, то магазин от его реализации получит прибыль р_j. Если же этот товар не будет пользоваться спросом, то издержки на его хранение принесут магазину убыток q_i. Требуется выбрать тип товара, который целесообразно завезти в магазин. В условиях неопределенного покупательского спроса конфликтная ситуация товароснабжения формализуется матричной игрой. Пусть первый игрок - магазин, второй игрок - покупательский спрос. Каждый из игроков имеет n стратегий. Завоз i-го товара - i-я стратегия первого игрока, спрос на j-й товар - j-я стратегия второго игрока. Тогда матрица выигрышей первого игрока имеет вид квадратной матрицы n-го порядка:

(1)