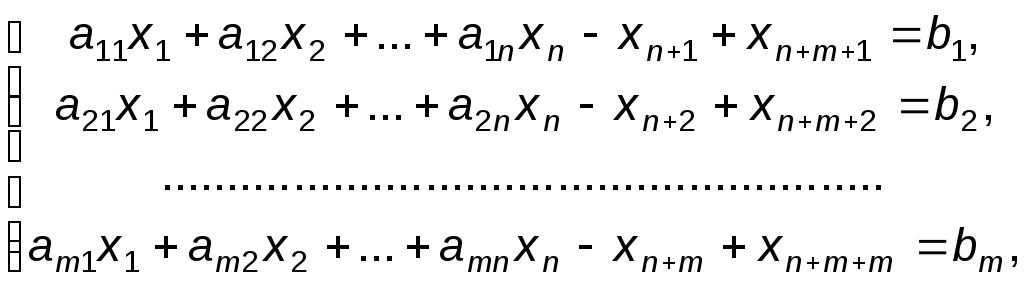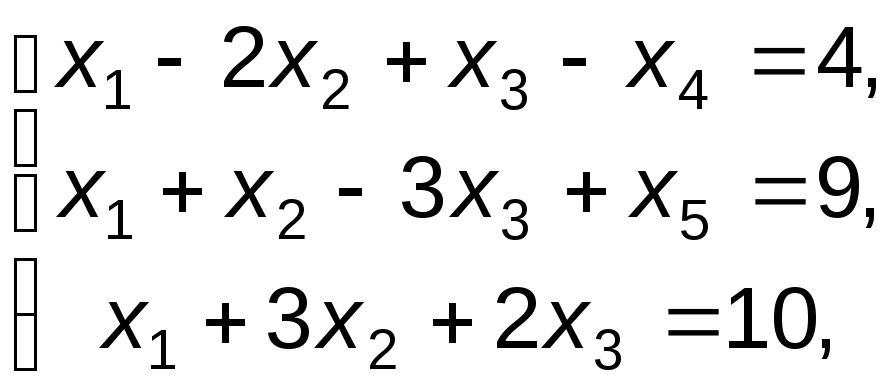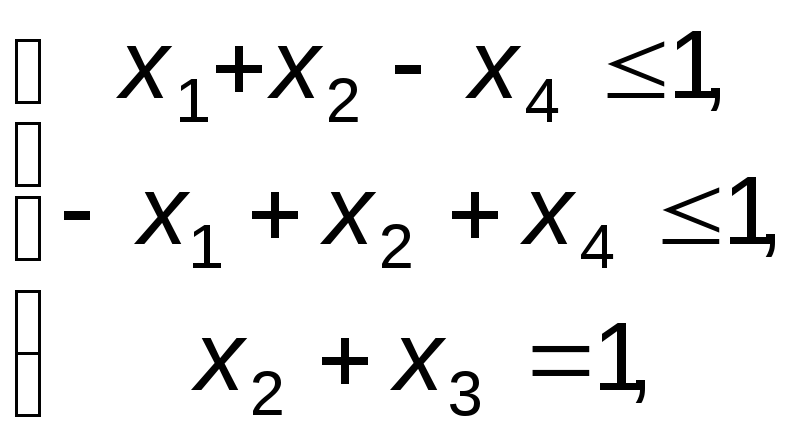5.7. Каноническая форма задач линейного программирования

Будем считать, что задача линейного программирования записана в канонической¹ форме, если ее целевая функция максимизируется, ограничения имеют вид равенств с неотрицательной правой частью и все переменные неотрицательны.

Задачи линейного программирования в канонической форме имеет вид:

(15)

Так как общая задача линейного программирования имеет ограничения не только вида "=", но и "", "", а целевая функция может либо максимизироваться, либо минимизироваться, то необходимо уметь приводить любые задачи линейного программирования к канонической форме. С этой целью рассмотрим два частных вида задач линейного программирования и покажем, как эти задачи привести к канонической форме.

Одна из частных задач линейного программирования может быть представлена моделью:

(16)

Левая часть каждого ограничения данной задачи меньше либо равна правой. Для того чтобы левая часть ограничения была равна правой, необходимо к левой части каждого ограничения прибавить соответственно неотрицательные переменные x_n+1, x_n+2, ..., x_n+m. Эти переменные вводятся в целевую функцию с нулевыми коэффициентами, что не изменить ее значение.

После приведения к канонической форме задача (16) будет иметь вид:

(17)

Переменные x_n+1, x_n+2, ..., x_n+m, называются дополнительными. Например, для задачи использования ресурсов, рассмотренной в §5.2 и модель которой (2) аналогична модели (16), дополнительные переменные будут экономически интерпретироваться как количество неиспользуемых ресурсов.

Рассмотрим другой частный вид задачи линейного программирования:

(18)

Определение минимального значения целевой функции f можно свести к определению максимального значения функции (-f), так как min f = -max (-f).

Для приведения ограничений вида "" к ограничениям-равенствам необходимо из левой части каждого ограничения вычесть соответственно неотрицательные переменные x_n+1, x_n+2, ..., x_n+m. Эти переменные вводятся в целевую функцию с нулевыми коэффициентами, чтобы не изменить ее значение.

После приведения к канонической форме задача (18) будет иметь вид:

(19)

Поскольку модель (18) аналогична модели задачи о диете (4), рассмотренной в §5.2, то для этой задачи дополнительные переменные будут экономически интерпретироваться как количество питательных веществ в смеси сверх заданного нижнего предела (b₁).

Таким образом, если в задаче линейного программирования определяется минимум целевой функции, то такую задачу необходимо свести к определению максимума целевой функции, а все имеющиеся ограничения вида "  " привести к ограничениям-равенствам.

5.8. Базисные решения задачи линейного программирования

Ранее отмечалось, что задача линейного программирования достигает своего оптимального решения в угловой точке многогранника решений. Координаты угловой точки - это базисное решение задачи. Определить базисное решение можно путем последовательных элементарных преобразований ограничений или специальными вычислительными приемами.

Рассмотрим ограничения задачи линейного программирования, записанной в канонической форме (15). Эти ограничения представляют собой систему m линейных уравнений с n переменными. Будем считать, что m<n, хотя на практике встречаются задачи, в которых m>n и m=n. Система совместна и ранг ее матрицы равен m.

В ограничениях задачи (15) все переменные можно разделить на две группы. Первая группа - основные (зависимые) переменные, число которых должно быть равно числу линейно независимых уравнений m, вторая - неосновные (независимые) переменные, число которых будет равно n-m. Такое разделение не связывается с индексами (порядковыми номерами) переменных.

Будем считать, что ограничения задачи (15), записанной в канонической форме, путем последовательных элементарных преобразований могут быть приведены к виду

(20)

где.

В системе (20) коэффициенты при каждом неизвестном x₁, x₂, ..., x_m образуют единичные векторы

,,...,.

Совокупность единичных векторов Е₁, Е₂, ..., Е_m образует базис m-мерного пространства, а переменные x₁, x₂, ..., x_m называются базисными. Переменная является базисной, если она входит только в одной из уравнений системы с коэффициентом, равным единице. Все остальные переменные являются небазисными.

Частное решение, полученное путем приравнивания небазисных (независимых) переменных нулю и нахождения значений базисных (зависимых) переменных, называется базисным решением. Следовательно, если x_m+1=0, x_m+2=0, ..., x_n=0, то x₁=b'₁, x₂=b'₂, ..., x_n=b'_m. Первое решение задачи, полученное таким образом, называется исходным базисным решением.

Базисное решение называется вырожденным, если значения одной или нескольких базисных переменных равны нулю. Задача, имеющая хотя бы одно вырожденное базисное решение, называется вырожденной, в противном случае - невырожденной.

При решении задачи линейного программирования базисные переменные, как правило, не выделяют путем последовательных элементарных преобразований, а пользуются специальными вычислительными приемами. Как известно, в задаче линейного программирования может встречаться три вида ограничений: "", "" и "=".

После приведения частной задачи, имеющей ограничения " (16), к канонической форме (17) каждое уравнение будет содержать базисную переменную, а именно x_n+1, x_n+2, ..., x_n+m. Приравняв небазисные переменные к нулю: x₁=0, x₂=0, ..., x_n=0, получим допустимое базисное решение:

xn+1=b1, xn+2=b2, ..., xn+m=bm

После приведения частной задачи, имеющей ограничения "" (18), к канонической форме (19) переменные x_n+1, x_n+2 ..., x_n+m не могут быть приняты в качестве базисных, так как они входят в уравнения с коэффициентом (-1). Поэтому для выделения базисных переменных и нахождения допустимого базисного решения используется метод искусственного базиса, который заключается в следующем.

В каждое ограничения задачи (19) вводятся соответственно искусственные неотрицательные переменные x_n+m+1, x_n+m+2, ..., x_n+m+m, которые принимаются в качестве базисных. Искусственные переменные входят в целевую функцию задачи с коэффициентом (-М), где М - большое положительное число, во много раз больше заданных в условии задачи.

После ввода искусственных переменных задача (19) принимает вид:

f=-c1x1-c2x2-...-cnxn+0 xn+1+0 xn+2+...+0 xn+m-M xn+m+1- -M xn+m+2-...-M xn+m+mmax; .

(21)

Искусственные переменные вводятся только с целью получения исходного базисного плана. Пока искусственная переменная является базисной, она будет принимать положительные значения (если соответствующие ей значения b_i>0) и, следовательно, уменьшать значение целевой функции по сравнению с максимальным. Поскольку эти переменные имеют большие по абсолютной величине отрицательные коэффициенты, в процессе решения задачи симплекс-методом они из числа базисных переводятся в небазисные. В силу того что значения небазисных переменных при получении базисного решения приравниваются к нулю, искусственные переменные не будут оказывать влияния на значение целевой функции.

Этот же метод используется для ограничений вида "=".

Замечание. При получении исходного базисного плана необходимо стремиться к тому, чтобы он содержал минимальное количество искусственных переменных. Это дает возможность уменьшить число шагов для получения оптимального решения.

Рассмотрим на конкретных примерах процесс приведения задачи линейного программирования к канонической форме и получения исходного базисного решения.

Пример 1. Привести к канонической форме следующую задачу линейного программирования:

f=2x1+x2-x3  max; x10, x20, x30.

Для приведения данной задачи к канонической форме необходимо из левой части первого ограничения вычесть неотрицательную переменную х₄, во втором ограничении - добавить х₅. Дополнительные переменные x₄ и x₅ в целевую функцию входят с нулевыми коэффициентами.

Каноническая форма данной задачи будет иметь вид:

f=2x1+x2-x3+0 x4+0 x5  max .

В первом и третьем ограничениях нельзя выделить базисные переменные, поэтому в первое ограничение вводим искусственную переменную x₆, а в третье - искусственную переменную x₇ и принимаем их в качестве базисных. В целевую функцию эти переменные войдут с коэффициентом (-М). В результате описанных преобразований получим:

f=2x1+x2-x3+0 x4+0 x5-М x6-M x7 max .

Для получения исходного базисного решения приравниваем к нулю небазисные переменные: x₁=0, x₂=0, x₃=0, x₄=0. Тогда значения базисных переменных: x₆=4, x₅=9, x₇=10. Подставив значения базисных переменных в целевую функцию, получим величину f=-14M.

Пример 2. Привести к канонической форме следующую задачу линейного программирования:

f=x1-x2-x3-x4  min .

Поскольку целевая функция данной задачи минимизируется, умножив ее выражение на (-1), получим:

f/=-x1+x2+x3+x4  max.

К левым частям первого и второго ограничений прибавим соответственно неотрицательные переменные x₅ и x₆, которые входят в целевую функцию с нулевыми коэффициентами. Тогда данная задача в канонической форме будет иметь вид:

f/=-x1+x2+x3+x4+0 x5+0 x6 max; .

В первом ограничения базисной является дополнительная переменная x₅, во втором - дополнительная переменная x₆.

В некоторых задачах в ограничениях вида "" и "=" базисные переменные можно выделить сразу, не прибегая к методу искусственного базиса. Третье ограничение рассматриваемой задачи содержит переменную x₃, которая не входит в другие ограничения. Эта переменная может быть принята в качестве базисной.

Для получения исходного базисного решения приравняем к нулю небазисные переменные: x₁=0, x₂=0, x₄=0 и получим значения базисных переменных: x₅=1, x₆=1, x₃=1. Значение целевой функции f=1.
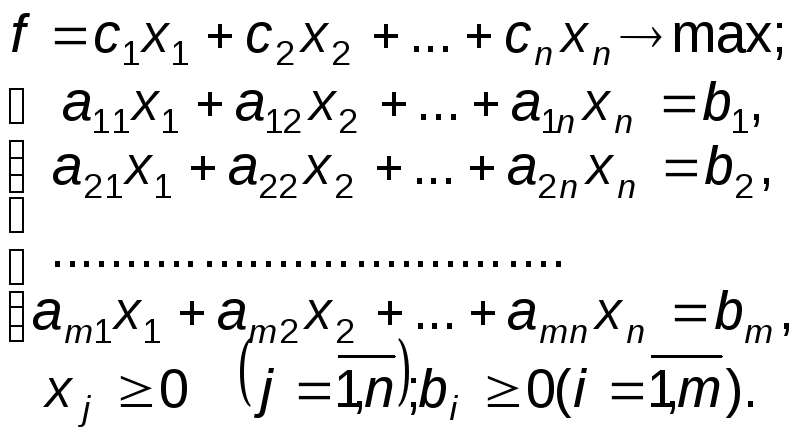
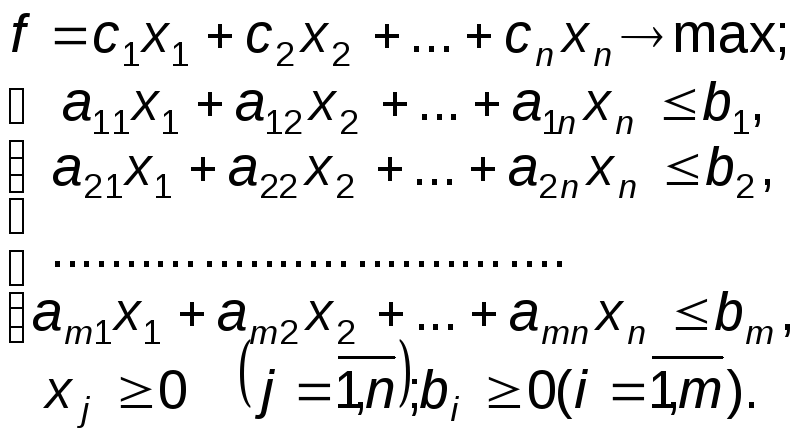
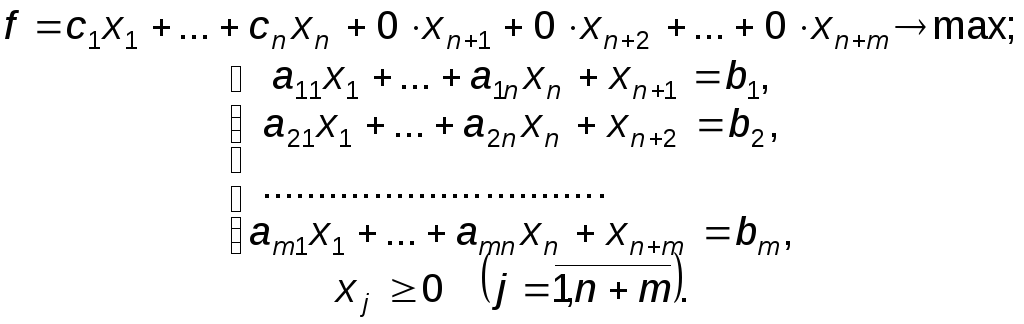
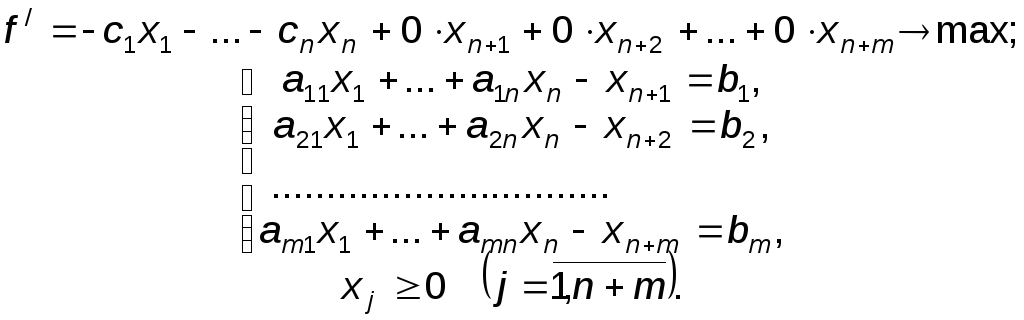
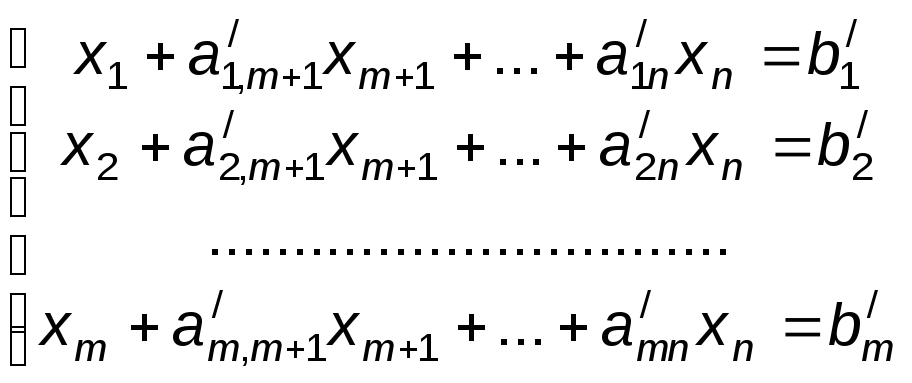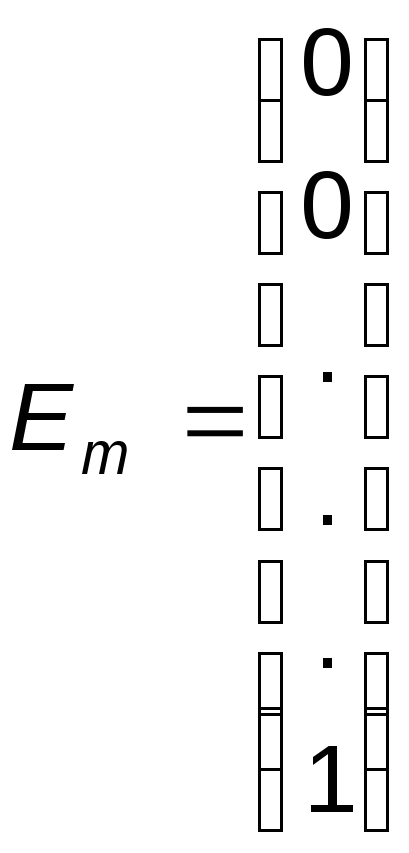