8.3.Методы решения задач дискретного программирования
Во всех случаях решение задачи, казалось бы, может быть найдено обычными методами с отброшенными условиями целочисленности и с последующими округлениями нецелых переменных в ответе. Однако такое округление может привести к решению, далекому от оптимального. Рассмотрим, например, геометрическую интерпретацию задачи дискретного линейного программирования (рис. 1).
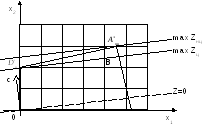
Рис. 1.
Оптимальным решением нецелочисленной задачи служит точка А*нц. Как следует из рис. 1, точка В ближе всего к точке А*нц в смысле округления. Но целой точкой, находящейся ближе всего к разрешающей линии уровня max Zнц, является точка D*ц. Таким образом, попытка решить задачу с отброшенным условием целочисленности и последующим округлением полученного оптимального плана до ближайших целых значений не всегда состоятельна. С практической точки зрения подобный подход допустим в тех случаях, когда значения переменных, образующих оптимальное решение исходной задачи, достаточно велики и погрешностями округления можно пренебречь.
В первом приближении методы целочисленной оптимизации можно разделить на две основные группы: точные и приближенные. К точным относятся методы отсечения и комбинаторные (метод ветвей и границ). Это универсальные методы дискретной оптимизации. Кроме универсальных, имеется много специальных точных методов, учитывающих специфику задачи.
Среди приближенных методов наметились два направления:
1) разработка детерминированных эвристических алгоритмов, учитывающих специфику задачи;
2) использование случайного поиска в сочетании с локальной оптимизацией.
8.3.1. Методы отсечения для решения полностью целочисленной задачи линейного программирования
Общая идея решения задачи дискретного программирования методами отсечения состоит в следующем. Исходная задача решается сначала без учета ограничений целочисленности. Если полученный оптимальный план удовлетворяет условиям целочисленности, то задача решена. В противном случае к ограничениям исходной задачи добавляется новое.
Затем задача решается с учетом нового ограничения. В случае необходимости добавляется еще одно ограничение и т.д. Геометрически добавление каждого нового ограничения отвечает проведению поверхности, которая отсекает от области допустимых решений некоторую его часть с оптимальной точкой с нецелыми координатами, но не затрагивает ни одной из целочисленных точек этого многогранника.
На основе этой идеи американский математик Р. Гомори предложил ряд сходящихся алгоритмов решения задач дискретного линейного программирования. Ему удалось обосновать правила построения дополнительных ограничений и доказать конечность алгоритмов.
Для лучшего понимания идеи методов отсечения обратимся к наглядной иллюстрации случая n=2 (рис. 2).
Рис. 2.
Ограничения задачи определяют на плоскости х1Ох2 некоторый многоугольник М, в вершине х*(1)нц которого, если не учитывать условия целочисленности, достигается максимум целевой функции.
Внутри этого многоугольника имеется конечное множество точек, которым соответствуют решения с целочисленными значениями переменных (на рисунке они обозначены кружочками). На рисунке показаны три прямые l1, l2, l3, соответствующие трем дополнительным линейным ограничениям. Каждая из прямых отсекает часть области допустимых решений. Так, после отсечения части области прямой оптимальной оказывается вершина х*(2)нц , затем х*(3)нц , и, наконец, оптимальной становится целочисленная вершина х*нц . Основное в алгоритме - составление дополнительного ограничения, т.е. отсекающей гиперплоскости, которая называется правильным отсечением. Правильное отсечение должно удовлетворять следующим условиям:
1) быть линейным;
2) отсекать найденное оптимальное нецелочисленное решение исходной задачи;
3) не отсекать ни одной из целочисленных точек исходной задачи.