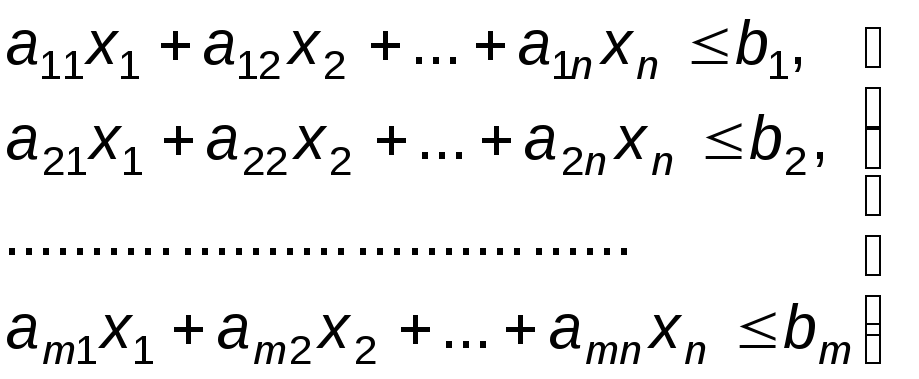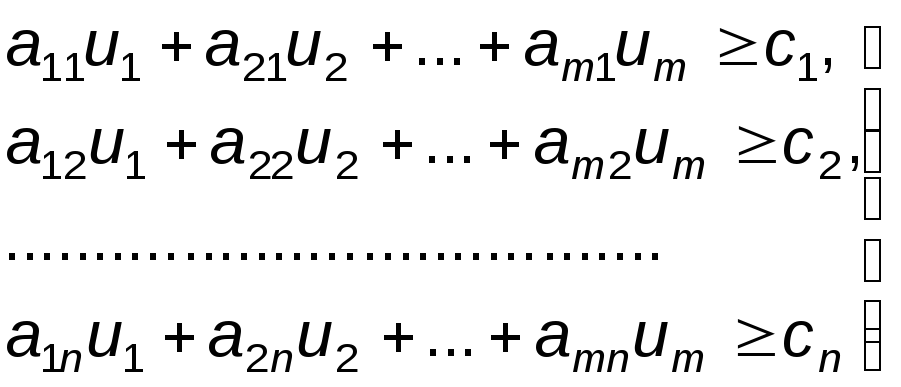- •Содержание
- •Введение
- •Тема 1. Экономико-математические методы и модели и их классификация
- •1.1. Социально-экономические системы, методы их исследования и моделирования
- •1.2.Этапы экономико-математического моделирования, классификация экономико-математических моделей и методов
- •Примеры описательных моделей
- •Тема 2. Балансовый метод в экономике
- •2.1. Общие понятия балансового метода, принципиальная схема межпродуктового баланса
- •2.2. Экономико-математическая модель межотраслевого баланса
- •2.3. Плановые расчеты на основе матричных моделей систем производства и распределения продукции
- •2.3.1. Методика расчета планового баланса по заданным валовым выпускам продукции Xiпл
- •2.3.2. Коэффициенты полных материальных затрат и методы их расчета
- •2.3.3. Методика расчета планового баланса по заданным плановым уровням конечной продукции Yiпл
- •2.4. Пример расчета планового баланса для трехотраслевой экономической системы
- •2.5. Использование балансового метода на предприятии
- •Тема 3. Математические методы сетевого планирования и управления
- •3.1. Основные понятия сетевой модели
- •Распределение (расслоение) вершин сетевого графика по рангам
- •3.2. Анализ сетевого графика и расчет его временных характеристик
- •3.2.1. Расчет временных характеристик событий
- •3.2.2. Расчет временных характеристик работ
- •3.3. Сетевое планирование в условиях неопределенности
- •Вероятностные оценки продолжительности работ
- •3.4. Оптимизация сетевой модели
- •Краткая характеристика метода оптимизации
- •Тема 4. Классификация задач математического программирования и область их эффективного применения в экономике
- •4.1. Математическая постановка и структура задачи оптимизации
- •4.2. Краткая классификация методов математического программирования
- •Тема 5. Линейное программирование
- •5.1. Предмет линейного программирования
- •5.2. Построение оптимизационных моделей для решения экономических задач
- •5.3. Общая задача линейного программирования. Основные определения
- •5.4. Графический метод решения задач линейного программирования
- •I этап. Графическая интерпретация области допустимых решений
- •II этап. Графическая интерпретация целевой функции
- •III этап. Нахождение оптимального решения
- •5.5. Примеры решения задач линейного программирования графическим методом
- •5.6. Понятие о симплекс-методе озлп
- •5.7. Каноническая форма задач линейного программирования
- •5.8. Базисные решения задачи линейного программирования
- •5.9. Алгоритм симплекс-метода озлп
- •5.10.Примеры решения задач линейного программирования симплекс-методом
- •Тема 6. Двойственность в линейном программировании
- •6.1.Понятие двойственности. Построение двойственных задач и их свойства
- •6.2. Основные теоремы двойственности и их экономическое содержание
- •Первая теорема двойственности
- •Вторая теорема двойственности (теорема о дополняющей нежесткости)
- •6.3.Экономическая интерпретация двойственной задачи Пример 1. Задача оптимального использования ресурсов.
- •6.4.Экономико-математический анализ полученных оптимальных решений
- •Свойство 1. Оценки как мера дефицитности ресурсов
- •Свойство 2. Оценки как мера влияния ограничений на функционал
- •Свойство 3. Оценки - инструмент определения эффективности отдельных вариантов (технологических способов) с позиций общего оптимума
- •Тема 7. Транспортная задача линейного программирования
- •7.1. Постановка транспортной задачи
- •Классическая постановка транспортной задачи
- •Модели транспортной задачи
- •7.2.Методы построения исходного плана
- •Метод северо-западного угла
- •Метод минимального элемента
- •7.3.Оптимизация исходного базисного плана перевозок. Метод потенциалов
- •Основные процедуры метода потенциалов
- •Алгоритм метода потенциалов
- •7.4. Пример решения транспортной задачи
- •7.5. Применение модели транспортной задачи при решении различных экономических задач
- •Тема 8. Модели и методы дискретного программирования
- •8.1. Постановка задачи дискретного программирования
- •Задача о назначении (проблема выбора, задача о женихах и невестах)
- •8.2.Краткая классификация математических моделей дискретного программирования
- •8.3.Методы решения задач дискретного программирования
- •8.3.1. Методы отсечения для решения полностью целочисленной задачи линейного программирования
- •8.3.2.Сущность метода ветвей и границ
- •Тема 9. Модели и методы динамического программирования
- •9.1. Моделирование процессов наилучшего распределения ресурсов методом динамического программирования
- •Итоговая таблица условно-оптимальных решений
- •Графики предельной и средней эффективности
- •Тема 10. О других моделях и методах математического программирования
- •10.1.Нелинейное программирование
- •10.2.Стохастическое программирование
- •Тема 11. Модели конфликтных ситуаций в теории игр
- •11.1.Основные понятия теории игр
- •11.2.Решение игры в чистых стратегиях
- •11.3.Решение игры без седловой точки
- •Графический способ решения матричной игры
- •11.4. Пример решения экономической задачи методами теории игр
- •Тема 12. Модели управления запасами
- •12.1. Основные понятия
- •12.2. Статические модели управления запасами Уилсона
- •12.2.1. Статическая модель без дефицита
- •12.2.2. Статическая модель с дефицитом
- •12.3. Модели со случайным спросом
- •Тема 13. Модели массового обслуживания
- •Литература
Тема 6. Двойственность в линейном программировании
6.1.Понятие двойственности. Построение двойственных задач и их свойства
Одним из направлений в математическом моделировании экономических задач является использование свойств двойственной задачи, которая может быть сформулирована для любой задачи на оптимум. Хорошо разработанный математический аппарат линейного программирования позволяет не только получать с помощью эффективных вычислительных процедур оптимальный план, но также сделать ряд экономически содержательных выводов, основанных на свойствах задачи, двойственной к исходной задаче линейного программирования (ЗЛП), т.е. послеоптимизационный анализ.
Понятие двойственности
рассмотрим на примере задачи оптимального
использования сырья. Пусть на предприятии
решили рационально использовать отходы
основного производства. В плановом
периоде появились отходы сырья m
видов в объемах bi
единиц (i=![]() ).
Из этих отходов, учитывая специализацию
предприятия, можно наладить выпуск n
видов неосновной продукции. Обозначим
через aij
норму расхода сырья i-го
вида на единицу j-й (j=
).
Из этих отходов, учитывая специализацию
предприятия, можно наладить выпуск n
видов неосновной продукции. Обозначим
через aij
норму расхода сырья i-го
вида на единицу j-й (j=![]() )
продукции, сj - цена
реализации единицы j-й
продукции (реализация обеспечена).
Неизвестные величины задачи: хj
- объемы выпуска j-й
продукции, обеспечивающие предприятию
максимум выручки.
)
продукции, сj - цена
реализации единицы j-й
продукции (реализация обеспечена).
Неизвестные величины задачи: хj
- объемы выпуска j-й
продукции, обеспечивающие предприятию
максимум выручки.
Математическая модель задачи:
|
|
(1) |
|
|
(2) |
|
|
(3) |
Дополнительная
переменная: yi
= bi -
aij
xj
(i=![]() )
)
Предположим далее, что с самого начала при изучении вопроса об использовании отходов основного производства на предприятии появилась возможность реализации их некоторой организации. Необходимо установить прикидочные оценки (цены) на эти отходы. Обозначим их u1, u2, ... um. Оценки должны быть установлены исходя из следующих требований, отражающих несовпадающие интересы предприятия и организации: 1) общую стоимость отходов сырья покупающая организация стремится минимизировать; 2) предприятие согласно уступить отходы только по таким ценам, при которых оно получит за них выручку, не меньшую той, что могло бы получить, организовав собственное производство. Эти требования формализуются в виде следующей ЗЛП.
Требование 1 покупающей организации - минимизация покупки:
|
|
(4) |
Требование 2 предприятия, реализующего отходы сырья, можно сформулировать в виде системы ограничений. Предприятие откажется от выпуска каждой единицы продукции первого вида, если:
|
|
|
где левая часть означает выручку за сырье, идущее на единицу продукции первого вида; правая - ее цену.
Аналогичные рассуждения легко провести в отношении выпуска продукции каждого вида. Поэтому требование предприятия, реализующего отходы сырья, можно формализовать в виде следующей системы ограничений:
|
|
(5) |
По смыслу задачи оценки должны быть неотрицательными:
|
|
(6) |
Переменные ui
(i=![]() )
называются двойственными оценками
или объективно обусловленными оценками.
В зарубежной литературе их еще называют
теневыми ценами.
)
называются двойственными оценками
или объективно обусловленными оценками.
В зарубежной литературе их еще называют
теневыми ценами.
Дополнительная
переменная:
![]()
Задачи (1)-(3) и (4)-(6) называются парой взаимно двойственных ЗЛП. Так как задачи (1)-(3) и (4)-(6) записаны в симметричной форме, их принято называть парой симметричных двойственных задач.
Пара взаимно двойственных симметричных задач в виде конечных сумм имеет вид:
|
Прямая задача |
Двойственная задача |
|
|
|
|
|
|
|
|
|
Согласно теории линейного программирования каждой ЗЛП вида (1)-(3) соответствует двойственная ей ЗЛП: (4)-(6).
Можно показать, что если в качестве прямой принять задачу (4)-(6) об определении оптимальных оценок на сырье, то двойственной к ней будет задача (1)-(3) об определении оптимального плана выпуска продукции.
Из моделей (1)-(3) и (4)-(6) непосредственно видно, что, имея математическую модель одной из этих задач, можно легко построить модель двойственной к ней задачи. Сопоставляя модели (1)-(3) и (4)-(6) пар двойственных задач, можно установить следующие взаимосвязи.
1. Если прямая задача на максимум, то двойственная к ней - на минимум, и наоборот.
2. Если прямая
задача на максимум, то ее система
ограничений представляется в виде
неравенств типа
![]() .
Двойственная задача решается на минимум,
и ее система ограничений имеет вид
неравенств типа
.
Двойственная задача решается на минимум,
и ее система ограничений имеет вид
неравенств типа
![]() .
.
3. Свободные члены bi ограничений прямой задачи являются коэффициентами целевой функции двойственной.
4. Коэффициенты сj целевой функции прямой задачи являются свободными членами ограничений двойственной задачи.
5. Матрицы коэффициентов ограничений прямой и двойственной задач являются транспонированными друг к другу.
6. Число ограничений прямой задачи равно числу переменных двойственной, а число ограничений двойственной - числу переменных прямой.
7. Все переменные в обеих задачах неотрицательны.
Двойственная задача со смешанными ограничениями составляется с соблюдением следующих дополнительных правил.
1. Если на переменную xj прямой задачи наложено условие неотрицательности, то j-е условие системы ограничений двойственной задачи записывается в виде неравенства, и наоборот.
2. Если на переменную xj прямой задачи не наложено условие неотрицательности, то j-е ограничение двойственной задачи записывается в виде строгого равенства.
3. Если в прямой задаче имеются ограничения равенства, то на соответствующие переменные двойственной задачи не налагается условие неотрицательности.
Очевидно, что задача, двойственная двойственной, совпадает с исходной. Поэтому безразлично, какую задачу принять в качестве прямой, а какую - двойственной. Следует говорить о паре взаимно двойственных задач.